


3.3. The Cosmic Microwave Background
Most of the radiation we observe in the universe today is in the form of an almost isotropic blackbody spectrum, with temperature approximately 2.7K, known as the Cosmic Microwave Background (CMB). The small angular fluctuations in temperature of the CMB reveal a great deal about the constituents of the universe, as we now discuss.
We have mentioned several times the way in which a radiation gas evolves in and sources the evolution of an expanding FRW universe. It should be clear from the differing evolution laws for radiation and dust that as one considers earlier and earlier times in the universe, with smaller and smaller scale factors, the ratio of the energy density in radiation to that in matter grows proportionally to 1 / a(t). Furthermore, even particles which are now massive and contribute to matter used to be hotter, and at sufficiently early times were relativistic, and thus contributed to radiation. Therefore, the early universe was dominated by radiation.
At early times the CMB photons were easily energetic enough to ionize hydrogen atoms and therefore the universe was filled with a charged plasma (and hence was opaque). This phase lasted until the photons redshifted enough to allow protons and electrons to combine, during the era of recombination. Shortly after this time, the photons decoupled from the now-neutral plasma and free-streamed through the universe.
In fact, the concept of an expanding universe provides us with a clear explanation of the origin of the CMB. Blackbody radiation is emitted by bodies in thermal equilibrium. The present universe is certainly not in this state, and so without an evolving spacetime we would have no explanation for the origin of this radiation. However, at early times, the density and energy densities in the universe were high enough that matter was in approximate thermal equilibrium at each point in space, yielding a blackbody spectrum at early times.
We will have more to say about thermodynamics in the expanding
universe in our next lecture. However, we should point out one crucial
thermodynamic fact about the CMB. A blackbody distribution, such as
that generated in the early universe, is such that at temperature T,
the energy flux in the frequency range
[ ,
,
 +
d
+
d ] is given by
the Planck distribution
] is given by
the Planck distribution
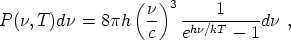 |
(59) |
where h is Planck's constant and k is the Boltzmann constant.
Under a rescaling 


 , with
, with
 = constant,
the shape of the spectrum is unaltered if
T
= constant,
the shape of the spectrum is unaltered if
T  T /
T /
 . We
have already seen that wavelengths are stretched with the cosmic
expansion, and therefore that frequencies will scale inversely due to
the same effect. We therefore conclude that the effect of cosmic
expansion on an initial blackbody spectrum is to retain its blackbody
nature, but just at lower and lower temperatures,
. We
have already seen that wavelengths are stretched with the cosmic
expansion, and therefore that frequencies will scale inversely due to
the same effect. We therefore conclude that the effect of cosmic
expansion on an initial blackbody spectrum is to retain its blackbody
nature, but just at lower and lower temperatures,
 |
(60) |
This is what we mean when we refer to the universe cooling as it expands. (Note that this strict scaling may be altered if energy is dumped into the radiation background during a phase transition, as we discuss in the next lecture.)
The CMB is not a perfectly isotropic radiation bath. Deviations from isotropy at the level of one part in 105 have developed over the last decade into one of our premier precision observational tools in cosmology. The small temperature anisotropies on the sky are usually analyzed by decomposing the signal into spherical harmonics via
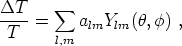 |
(61) |
where alm are expansion coefficients and
 and
and
 are spherical
polar angles on the sky. Defining the power spectrum by
are spherical
polar angles on the sky. Defining the power spectrum by
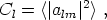 |
(62) |
it is conventional to plot the quantity l (l + 1)Cl against l in a famous plot that is usually referred to as the CMB power spectrum. An example is shown in figure (3.6), which shows the measurements of the CMB anisotropy from the recent WMAP satellite, as well as a theoretical model (solid line) that fits the data rather well.
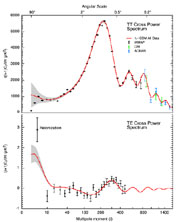 |
Figure 3.6. The CMB power spectrum from the
WMAP satellite
[72].
The error bars on this plot are
1- |
These fluctuations in the microwave background are useful to cosmologists for many reasons. To understand why, we must comment briefly on why they occur in the first place. Matter today in the universe is clustered into stars, galaxies, clusters and superclusters of galaxies. Our understanding of how large scale structure developed is that initially small density perturbations in our otherwise homogeneous universe grew through gravitational instability into the objects we observe today. Such a picture requires that from place to place there were small variations in the density of matter at the time that the CMB first decoupled from the photon-baryon plasma. Subsequent to this epoch, CMB photons propagated freely through the universe, nearly unaffected by anything except the cosmic expansion itself.
However, at the time of their decoupling, different photons were released from regions of space with slightly different gravitational potentials. Since photons redshift as they climb out of gravitational potentials, photons from some regions redshift slightly more than those from other regions, giving rise to a small temperature anisotropy in the CMB observed today. On smaller scales, the evolution of the plasma has led to intrinsic differences in the temperature from point to point. In this sense the CMB carries with it a fingerprint of the initial conditions that ultimately gave rise to structure in the universe.
One very important piece of data that the CMB fluctuations give us is
the value of
 total.
Consider an overdense region of
size R, which therefore contracts under self-gravity over a
timescale R (recall c = 1). If
R >> HCMB-1 then the
region will not have had time to collapse over the lifetime of the
universe at last scattering. If
R << HCMB-1 then collapse
will be well underway at last scattering, matter will have had time to
fall into the resulting potential well and cause a resulting rise in
temperature which, in turn, gives rise to a restoring force from
photon pressure, which acts to damps out the inhomogeneity.
total.
Consider an overdense region of
size R, which therefore contracts under self-gravity over a
timescale R (recall c = 1). If
R >> HCMB-1 then the
region will not have had time to collapse over the lifetime of the
universe at last scattering. If
R << HCMB-1 then collapse
will be well underway at last scattering, matter will have had time to
fall into the resulting potential well and cause a resulting rise in
temperature which, in turn, gives rise to a restoring force from
photon pressure, which acts to damps out the inhomogeneity.
Clearly, therefore, the maximum anisotropy will be on a scale which
has had just enough time to collapse, but not had enough time to
equilibrate -
R ~ HCMB-1. This means that we expect to
see a peak in the CMB power spectrum at an angular size corresponding
to the horizon size at last scattering. Since we know the physical
size of the horizon at last scattering, this provides us with a ruler
on the sky. The corresponding angular scale will then depend on the
spatial geometry of the universe. For a flat universe (k = 0,
 total =
1) we expect a peak at
l
total =
1) we expect a peak at
l  220 and, as can
be seen in figure (3.6), this is in excellent
agreement with observations.
220 and, as can
be seen in figure (3.6), this is in excellent
agreement with observations.
Beyond this simple heuristic description, careful analysis of all of the features of the CMB power spectrum (the positions and heights of each peak and trough) provide constraints on essentially all of the cosmological parameters. As an example we consider the results from WMAP [73]. For the total density of the universe they find
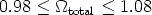 |
(63) |
at 95% confidence - as mentioned, strong evidence for a flat universe. Nevertheless, there is still some degeneracy in the parameters, and much tighter constraints on the remaining values can be derived by assuming either an exactly flat universe, or a reasonable value of the Hubble constant. When for example we assume a flat universe, we can derive values for the Hubble constant, matter density (which then implies the vacuum energy density), and baryon density:
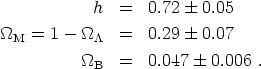 |
If we instead assume that the Hubble constant is given by the
value determined by the HST key project (53), we can
derive separate tight constraints on
 M and
M and

 ;
these are shown graphically in
Figure 3.7, along with constraints from the
supernova experiments.
;
these are shown graphically in
Figure 3.7, along with constraints from the
supernova experiments.
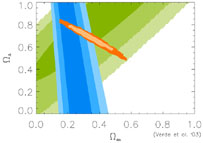 |
Figure 3.7. Observational constraints in
the
|
Taking all of the data together, we obtain a remarkably consistent picture of the current constituents of our universe:
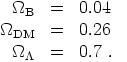 |
(64) |
Our sense of accomplishment at having measured these numbers is substantial, although it is somewhat tempered by the realization that we don't understand any of them. The baryon density is mysterious due to the asymmetry between baryons and antibaryons; as far as dark matter goes, of course, we have never detected it directly and only have promising ideas as to what it might be. Both of these issues will be discussed in the next lecture. The biggest mystery is the vacuum energy; we now turn to an exploration of why it is mysterious and what kinds of mechanisms might be responsible for its value.