5.7. Solving the Problems of the Standard Cosmology

Let's stick with the simple model of the last section. It is rather easy to see that the Einstein equations are solved by

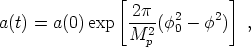(213)

as we might expect in inflation. The period of time during which (208) is valid ends at t ~ t, at which

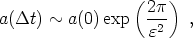(214)

Now, taking a typical value for m, for which < 10^-4, we obtain

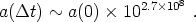(215)

This has a remarkable consequence. A proper distance L_P at t = 0 will inflate to a size 10¹⁰⁸cm after a time t ~ 5 × 10^-36 seconds. It is important at this point to know that the size of the observable universe today is H₀^-1 ~ and has not had enough 10²⁸ cm! Therefore, only a small fraction of the original Planck length comprises today's entire visible universe. Thus, homogeneity over a patch less than or of order the Planck length at the onset of inflation is all that is required to solve the horizon problem. Of course, if we wait sufficiently long we will start to see those inhomogeneities (originally sub-Planckian) that were inflated away. However, if inflation lasts long enough (typically about sixty e-folds or so) then this would not be apparent today. Similarly, any unwanted relics are diluted by the tremendous expansion; so long as the GUT phase transition happens before inflation, monopoles will have an extremely low density.

Inflation also solves the flatness problem. There are a couple of ways to see this. The first is to note that, assuming inflation begins, the curvature term in the Friedmann equation very quickly becomes irrelevant, since it scales as a(t)^-2. Of course, after inflation, when the universe is full of radiation (and later dust) the curvature term redshifts more slowly than both these components and will eventually become more important than both of them. However, if inflation lasts sufficiently long then even today the total energy density will be so close to unity that we will notice no curvature.

A second way to see this is that, following a similar analysis to that leading to (173) leads to the conclusion that = 1 is an attractor rather than a repeller, when the universe is dominated by energy with w < - 1/3. Therefore, is forced to be very close to one by inflation; if the inflationary period lasts sufficiently long, the density parameter will not have had time since to stray appreciably away from unity.