1. SINGLE-DISH AND INTERFEROMETRIC OBSERVATIONS

Radiometric observations using single dishes and interferometers are responsible for most detections of the Sunyaev-Zel'dovich (SZ) effects. This article discusses the techniques used in measuring the thermal and kinematic SZ effects in this way, the pitfalls that may arise, the systematic errors in the data, and the resulting uncertainties in the interpretation of the results. Since these uncertainties limit the physics return from SZ effect research, some approaches that would improve this situation are described. Longer reviews of SZ effect research (Rephaeli 1995; Birkinshaw 1999; Carlstrom, Holder Reese 2002) may be consulted for additional details.

1.1. Radiometric quantities

In discussing radiometric observations it is conventional to work with the flux density (S, the energy received per unit time per unit frequency per unit area) as the measure of the brightness of an unresolved source. However, the SZ effects of clusters of galaxies are extended, and so a measure of surface brightness is more appropriate. Two such quantities are in general use. The flux density per unit solid angle, , is commonly adopted in describing interferometric observations, where the solid angle is usually the area of the synthesized beam. The brightness temperature, T_RJ, is more usual in single-dish work.

Flux density per unit solid angle and brightness temperature are related by

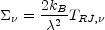(1)

where and T_RJ, are functions of both frequency and position. is the wavelength corresponding to frequency , and k_B = 1.38 × 10^-23 J K^-1 is the Boltzmann constant. Eq. (1) can be seen to be based on the Rayleigh-Jeans approximation for black-body radiation (hence the use of the RJ suffix). The specific intensity, I, the energy per unit time per unit frequency per unit area of the detector per unit solid angle, of black-body radiation is given by the Planck law

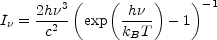(2)

so that at low frequencies (h << k_BT) T_RJ, = T, the thermodynamic (radiation) temperature. Nevertheless, the definition of eq. (1) for brightness temperature is used even at high frequencies, where T_RJ, < T.

It is important to bear in mind this use of brightness temperature because observations of primordial fluctuations in the microwave background radiation (MBR) normally quote results in terms of fractional changes in the thermodynamic temperature T / T, rather than T_RJ, / T_RJ,, or even T_RJ, / T. The relationships between these quantities are complicated for the thermal SZ effect.

It will also be necessary to discuss the polarization of the SZ effects. Polarization in radio astronomy is generally described by the (I, Q, U, V) Stokes parameters. I is the specific intensity already described, and measures the total energy arriving from the source. (Q, U) describe that part of the energy arriving from the source that is linearly polarized, with a positive value for Q corresponding to vertically polarized radiation dominating over the horizontal polarization. 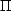(I, Q, U) together can be used to calculate the linearly polarized flux density fraction, , and its position angle, ,

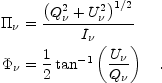(3a) (3b)

while the circular polarization Stokes parameter, V, will not be of interest in this article.

It is useful to express the flux density/brightness temperature relationship for the thermal SZ effect in the usual units of radio astronomy, as

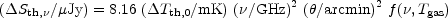(4)

where f (, T_gas) is the spectrum of the SZ effect in brightness temperature terms, normalized to its value at zero frequency. In the Kompaneets approximation,

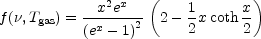(5)

where x = h / k_B T, and f is independent of the temperature of the gas in the cluster, T_gas. A more precise description of the scattering process (Rephaeli 1995), shows that f is a function of both and T_gas, and that there are deviations of the spectrum from eq. (5) at high temperature. T_{th, 0} is the zero-frequency brightness temperature change between a line of sight through a cluster and an average line of sight that sees only the unscattered MBR, while S_th, is the flux density difference at frequency caused by the thermal SZ effect. A rich cluster of galaxies with k_B T_gas = 5 keV might have a central thermal SZ effect T_{th, 0} = - 0.5 mK at zero frequency. A region with angular radius = 0.5 arcmin in the central part of the cluster will then appear with a flux density S_th, = - 0.9 mJy at 30 GHz (where T_th, = - 0.48 mK), -6.4 mJy at 110 GHz (-0.26 mK), and +11.0 mJy at 350 GHz (+0.04 mK) after a null in either flux density or brightness temperature terms at about 218 GHz.

The corresponding kinematic SZ effect, T_kin, is smaller than the thermal effect by a factor

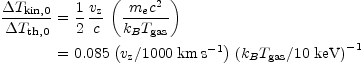(6a) (6b)

at low frequency. Thus if the cluster with k_B T_gas = 5 keV and T_{th, 0} = - 0.5 mK is moving away from the observer with a peculiar radial velocity v_z = 1000 km s^-1, the kinematic effect will produce signals in a region with angular radius 0.5 arcmin of S_kin, = - 0.15 mJy ( T_kin, = - 83 µK) at 30 GHz, -1.6 mJy (-63 µK) at 110 GHz, and -1.7 mJy (-7 µK) at 350 GHz, with a maximum flux density effect of -2.8 mJy (-28 µK) near the null of the thermal effect, at about 218 GHz.

While the flux densities for the thermal and kinematic effects are not small by comparison with the sensitivities achievable by (for example) the Very Large Array (VLA) or Australia Telescope Compact Array (ATCA) in a few hours of observing, the relatively large angular sizes on which the effects appear cause considerable difficulties in their detection, as will become apparent later.

Polarization SZ effects arise from a number of causes, including multiple inverse-Compton scatterings within clusters and the transverse or radial peculiar motions of clusters. Recent discussions of polarization terms have been given by Challinor, Ford, Lasenby (2000), and values

(7)

where _e is the inverse-Compton scattering optical depth (normally less than 10^-2) are typical for multiple scatterings in even the richest clusters of galaxies. Even smaller effects are obtained from single scatterings of the quadrupolar anisotropy, or multiple scatterings of the dipole anisotropy, induced by cluster motions. The detection of such small effects is not yet possible, and so their study must await the development of specialized SZ effect telescopes (Sec. 4.3). Nevertheless, such polarization signals would be of considerable interest since they probe the kinematics of clusters, and so provide information not otherwise available about the development of large-scale structure.

As a final element of jargon associated with SZ observing, it is important to distinguish between the brightness temperature, T_RJ, associated with the properties of the radiation field, and the antenna temperature, T_A, measured by a radio telescope. T_A and T_RJ are related by an efficiency factor which depends on the ability of the telescope to detect incoming radiation and the relative sizes and shapes of the telescope beam and the source on the sky. For our present purposes we will regard the relationship between the absolute brightnesses of structures seen on the sky and the detected radio power to be a matter of absolute calibration embedded in a generic gain factor G.