


3.3. Distance of CL 0016+16
We can apply the formalism derived in the discussion of the Hubble
diagram (Sec. 2.6) to estimate the distance
of the cluster. The X-ray emission measure of CL 0016+16, integrated
over the entire best-fitting
 model, is
model, is
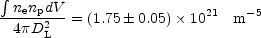 |
(37) |
and for the isothermal
 model we
expect that
model we
expect that
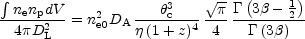 |
(38) |
(as in eq. (31),
where  is the
electron/proton ratio, taken as being constant
over the entire cluster. Since the X-ray data measure
is the
electron/proton ratio, taken as being constant
over the entire cluster. Since the X-ray data measure
 and
and
 c from the
structure of the atmosphere,
c from the
structure of the atmosphere,
 (which
depends on the abundance of metals in the gas) and
Tgas from
the X-ray spectrum, and the redshift is available either from the
X-ray spectrum or optical measurements, the emission measure implies a
value for the combination
ne02 DA of the unknown
central gas density in the cluster and its angular diameter distance.
(which
depends on the abundance of metals in the gas) and
Tgas from
the X-ray spectrum, and the redshift is available either from the
X-ray spectrum or optical measurements, the emission measure implies a
value for the combination
ne02 DA of the unknown
central gas density in the cluster and its angular diameter distance.
The central SZ effect of
 TRJ,
0 = - 1.26 ± 0.07 mK measures a
different combination of gas properties and distance,
TRJ,
0 = - 1.26 ± 0.07 mK measures a
different combination of gas properties and distance,
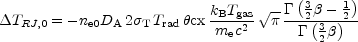 |
(39) |
and so ne0 DA can be derived from the SZ data. These results can therefore be combined to produce measurements of DA and ne0.
The distance of CL 0016+16 that results is
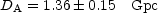 |
(40) |
where the error, at present, is random only. The largest contribution to this random error come from the error on the amplitude of the SZ effect (about 6%, which leads to a 12% error in the distance): an improved measurement of the SZ effect in even this cluster, which has a relatively well-measured SZ effect, would immediately lead to a significant improvement in distance. However, the major issue in absolute distance measurements of this type is not the random error, which could be reduced by continued observations or similar-depth observations of a large number of clusters, but rather the systematic error.
Similarly, a cosmology-independent central electron density can be deduced by combining the X-ray and SZ effect data. The result
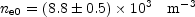 |
(41) |
has a significantly smaller random error than the distance because of the lower power of the SZ effect normalization that appears in the expression for ne0.
The systematic errors in the angular diameter distance that arise in
the application of this method are summarized in
Table III. The major issue for any individual cluster
is that of its unknown 3-D shape. Even if we take cluster shapes as
being simple oblate or prolate ellipsoids, the possible variations in
the estimated distance can be large (e.g.,
Hughes and Birkinshaw 1998).
Additional uncertainty in the X-ray and SZ effect form factors
arises because the X-ray measurements are principally sensitive to
the central cluster emission (since X-ray emissivity depends on
ne2), while the SZ effect is proportional to
ne, and so is relatively more sensitive to the outer
regions. Thus changes in shape between the inner and outer parts of
the cluster can produce an error in the distance which is effectively
unprobed by the X-ray profile even if the structure is
spherically-symmetric. For CL 0016+16, where an unusually deep
X-ray observation exists, the X-ray data probe to angles < 5 arcmin
from the centre, so that about 8 per cent of the central SZ effect
originates from larger radii and so is represented in the model used
to estimate distance only through an extrapolation of the
 model. The fraction of the gas that is unprobed is usually
substantially larger than this, leading to a larger potential problem
in relating the X-ray and SZ effect data to determine the distance.
model. The fraction of the gas that is unprobed is usually
substantially larger than this, leading to a larger potential problem
in relating the X-ray and SZ effect data to determine the distance.
Small-scale thermal and density substructure within the cluster can also affect the estimate of distance by boosting the X-ray output relative to the SZ effect (for example by isobaric clumping of the intracluster medium), or by boosting the SZ effect relative to the X-ray output (for example through the existence of regions of shock heating which can cause only small changes in the X-ray spectrum but large local enhancements in electron pressure). The upper limit on the amplitude of these effects in Table III is believed to be conservative, and could be reduced by improved X-ray spectroscopy. However, in a sense this problem could be improved by observing a sample of clusters, since it is unlikely that each will have the same level of substructure. Major outliers could then be detected and removed. For any individual cluster, only simple checks against the presence of substructure in the image (via deviations from Poisson statistics) or in the spectrum (via introducing a distribution of emission measures corresponding to different temperatures) can be made.
| Class of error | Component |
 D /
DA D /
DA |
| Calibration | SZ effect amplitude | 0.10 |
| X-ray emission measure | 0.05 | |
| X-ray temperature | < 0.02 | |
| Projection | 3-D shape of cluster | 0.20 |
| Substructure | Clumping, shocks, etc. | 0.15 |
| Contamination | Kinematic SZ, sources, etc. | 0.05 |
| Quadrature combination | 0.25 | |
Absolute distance measurements like this require absolute calibration of the data used to make the measurements, and so the ultimate reliability of the distances will depend on the reliability of the calibrations. The largest problem is likely to be in the calibration of the radio flux density scale (as described in Sec. 2.1.1), and efforts to improve the calibration of the scale at each of the frequencies used for SZ effect measurement are essential if the distances are to be free from systematic shifts in the distance scale which cannot be identified by sample studies.
If we combine the random and systematic errors on the distance, then the updated result for the angular diameter distance of CL 0016+16 from eq. (40) is
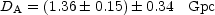 |
(42) |
where the first error is random, and the second systematic. This can be converted into a measurement of the Hubble constant if we make some assumption about the correct cosmology. Adopting a flat cold dark matter cosmology with a cosmological constant contributing 70% of the closure density, we find
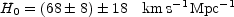 |
(43) |
which is consistent with the consensus distance scale. The larger
value than found in earlier results for CL 0016+16 (which gave a
result near 50 km s-1 Mpc-1) arises almost equally
from an increase in the temperature of the gas (from 7.5 to 9.1 keV)
and from the change from an open CDM to a flat
 CDM cosmology.
CDM cosmology.