3.5. Faraday Rotation effect

The Faraday rotation effect appears during the propagation of electromagnetic waves in a magnetized plasma. A linearly polarized wave can be decomposed into opposite-handed circularly polarized components. The right-handed and left-handed circularly polarized waves propagate with different phase velocities within the magneto-ionic material. This effectively rotates the plane of polarization of the electromagnetic wave.

According to the dispersion relation, for a wave of angular frequency ( = 2 ), the refractive index of a magnetized dielectric medium can take two possible values:

(35)

where _p = [(4 n_e e²) / (m_e)]^1/2 is the plasma frequency, and _e = (e B) / (m_e c) is the cyclotron frequency.

In the context of the study of cluster magnetic fields we are interested in the Faraday rotation of radio sources in the background of the cluster or in the cluster itself. The radio frequencies dominate the values of _p and _e obtained for typical magnetic fields (B 1 µG) and gas densities (n_e 10^-3 cm^-3) in the ICM. In the limit >> _e, Eq. 35 can be approximated as:

(36)

thus the difference in time of the two opposite handed waves to travel a path length dl results:

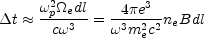(37)

and the phase difference between the two signals is = t. Therefore, traveling along the cluster path length L, the intrinsic polarization angle _Int will be rotated by an angle = 1/2 , resulting:

(38)

where B_|| is the component of the magnetic field along the line of sight. _Obs is usually written in terms of the rotation measure, RM:

(39)

where:

(40)

In practical units:

(41)

By convention, RM is positive (negative) for a magnetic field directed toward (away from) the observer.

The position angle of the polarization plane _Obs is an observable quantity, therefore, the RM of radio sources can be derived by a linear fit to Eq. 39. In general, the position angle must be measured at three or more wavelengths in order to determine RM accurately and remove the _Obs = _Obs ± n ambiguity.

3.5.1. Depolarization due to Faraday rotation

The term depolarization indicates a decrease of the polarization percentage, either at a given frequency, or when comparing two different frequencies. In a radio source the observed degree of polarization intensity, P_Obs(), can be significantly lower with respect to the intrinsic value, P_Int, if differential Faraday rotation occurs. The Faraday rotation can induce a depolarization of the observed radiation in different circumstances.

External depolarization is induced by the limitations of the instrumental capabilities. Beamwidth depolarization is due to the presence of fluctuations in the foreground screen within the observing beam: unresolved density or magnetic field inhomogeneities of the media through which the radiation propagates induce unresolved spatial variation in the Faraday rotation measure and hence beam depolarization. In addition, bandwidth depolarization occurs when a significant rotation of the polarization angle of the radiation is produced across the observing bandwidth.

Internal depolarization is due to the spatial extent of the source itself and occurs even if the intervening media are completely homogeneous. Along the line of sight, the emission from individual electrons within a source arises from different depths and suffers different Faraday rotation angles due to the different path length. For the total radiation emitted by the source, this results in a reduction of the observed degree of polarization. In the case that the Faraday effect originates entirely within the source, when the source can be represented by an homogeneous optically thin slab, the degree of polarization varies as [7]:

(42)

where RM' is the internal Rotation Measure through the depolarizing source. If a value of the Rotation Measure RM_Obs is derived observationally from the rotation of the polarization angle, then RM' in the above equation is = 2 RM_Obs [8, 9]. Indeed the observed rotation is the average of the full rotation occurring across the source, thus it is 1/2 of the total back-to-front rotation.

To distinguish between the external and internal depolarization, very high resolution and sensitive polarization data at multiple frequencies are needed. The key difference between them is that internal depolarization should be correlated with the Faraday rotation measure, therefore regions with small RM should exhibit very little depolarization. Instead, the external beam depolarization, due to gradients in the RM, should not be correlated with the amount of the RM but with the amount of the RM gradient.

3.5.2. Interpretation of the cluster RM data

RM data of radio sources in the background of clusters or in the clusters themselves, together with a model for the intracluster gas density distribution, can provide important information on the cluster magnetic field responsible for the Faraday effect. The Faraday effect of an external screen containing a gas with a constant density and a uniform magnetic field produces no depolarization and a rotation of the polarization angle proportional to ² <RM>, with:

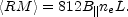(43)

The existence of small-scale magnetic field structures produce both rotation of the polarization angle and depolarization.

The effect of Faraday rotation from a tangled magnetic field has been analyzed by several authors [8, 9, 14, 15, 16, 17], in the simplest approximation that the magnetic field is tangled on a single scale _c. In this ideal case, the screen is made of cells of uniform size, electron density and magnetic field strength, but with a field orientation at random angles in each cell. The observed RM along any given line of sight is then generated by a random walk process involving a large number of cells of size _c. The distribution of the RM is Gaussian with <RM> = 0, and variance given by:

(44)

In this formulation, by considering a density distribution which follows a -profile [18]:

(45)

the following relation for the RM dispersion as a function of the projected distance from the cluster center, r, is obtained by integrating Eq. 44:

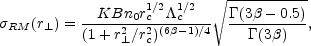(46)

where is the Gamma function. The constant K depends on the integration path over the gas density distribution: K = 624, if the source lies completely beyond the cluster, and K = 441 if the source is halfway through the cluster.

Therefore, since the density profile of the ICM can be obtained by X-ray observations, the cluster magnetic field strength can be estimated by measuring _RM from spatially resolved RM images of radio sources if _c is inferred or is known.