


2.1. Metallicity Gradients in Spiral Disks
Metallicity is the fraction by mass of all elements heavier than He in a system and is the primary indicator of chemical evolution as stars convert H into heavier elements and seed their environments with the products. Oxygen is the metallicity tracer of choice in the interstellar medium. Cosmically, its relative abundance surpasses all elements but H and He. Its relatively small depletion (Snow & Witt 1996; Savage & Sembach 1996) means it is present almost entirely in the gas phase. Hot, ionized gas in the vicinity of hot stars or energetic shock waves gives rise to H II regions, planetary nebulae, or supernova remnants whose spectra usually display prominent emission lines of oxygen. This contrasts sharply with the situation for old stars, for example, where absorption features of iron (heavily depleted onto grains in the interstellar medium) are prominent in stellar spectra due to the presence of optimal temperatures. Thus, iron is usually employed as a metallicity indicator when old stars are the probes.
Differences in the appearances of H II region spectra as a function of galactocentric distance were first noticed by Aller (1942) in his study of M33. Thirty years later, Searle (1971) connected similar differences across disks of several Sc galaxies with systematic changes in heavy-element abundances. Early abundance gradient work in spirals is reviewed by Pagel & Edmunds (1981), while the more contemporary picture is available in Friedli et al. (1998).
2.1.1. Metallicity Gradients in the Milky Way Galaxy
The disk of the Milky Way Galaxy (MWG) is arguably the most active and rapidly evolving region of our galaxy in the chemical sense. Probing it, though, is complicated by the presence of dust along all lines of sight within the disk, preventing radiation, particularly in the ultraviolet, from readily penetrating it. From our location within the disk, not only is the observation of emission-line objects restricted from the effects of reddening, but the presence of dust limits the distance over which we can probe. Despite these restrictions, large amounts of data are now available for H II regions and planetary nebulae within the disk of the MWG. The distance range from the Sun in both the directions of the Galactic center and anticenter has been extended by observations in the infrared, where extinction is at a minimum.
Table 1 summarizes the data for emission-line objects in the disk of the MWG and compiled here. The columns in order indicate the type of object and spectral region (optical, far-infrared, or radio) followed by the name of the first author on the paper for the data source, the total number of and Galactocentric distance range for objects included in each study, and finally an indication of the number of data points for each abundance ratio which were available in each study.
| Object | Author a | No. | Range (kpc) | O/H | N/O | Ne/O | S/O | Ar/O |
| H II (OPT,RAD) | Shaver | 21 | 5.9-13.7 | 21 | 20 | 9 | 7 | 16 |
| H II (FIR) | Simpson | 22 | 0.0-10.2 | 22 | 22 | 17 | 22 | |
| H II (FIR) | Afflerbach | 34 | 0.0-11.4 | 34 | 34 | 34 | ||
| H II (OPT) | Vílchez | 18 | 11.7-18.0 | 9 | 9 | 6 | ||
| H II (OPT) | Fich | 18 | 11.5-17.9 | 4 | 4 | 1 | ||
| H II (FIR) | Rudolph | 5 | 12.9-17.0 | 5 | 2 | 4 | ||
| PNe II (OPT) | Maciel | 91 | 4.6-12.4 | 91 | 76 | 77 | 73 | |
| SNR (OPT) | Fesen | 13 | 4.6-13.5 | 13 | 13 | 13 | ||
a Shaver: Shaver et al. (1983); Simpson: Simpson et al. (1995); Afflerbach et al. (1997); Vílchez: Vílchez & Esteban (1996); Fich: Fich & Silkey (1991); Rudolph: Rudolph et al. (1997); Maciel: Maciel & Köppen (1994); Fesen: Fesen, Blair, & Kirshner (1985) |
||||||||
Six of the eight studies in Table 1 are based upon H II regions. The seminal study by Shaver et al. (1983) explored a range in Galactocentric distance centered on the Sun. More recent studies by Fich & Silkey (1991), Vílchez & Esteban (1996), and Rudolph et al. (1997) focused on the anticenter direction, while Simpson et al. (1995) and Afflerbach, Churchwell, & Werner (1997) studied objects toward the center of the Galaxy. Although the optical studies were all ground based, the far-infrared work in all three cases was carried out using the Cryogenic Grating Spectrometer aboard the Kuiper Airborne Observatory to observe emission lines such as [N III] 57 µm, [O III] 52, 88 µm, and [S III] 19, 33 µm.
The remaining two papers in Table 1 were based on studies of planetary nebulae (Maciel & Köppen 1994) and supernova remnants (Fesen, Blair, & Kirshner 1985). Planetary nebulae (PNe) comprise ejected material from evolved intermediate-mass stars and thus generally have an abundance profile which differs somewhat from that of the progenitor star at the time of birth as a result of contamination of the nebula by products of stellar nucleosynthesis. However, the contamination affects primarily helium, carbon, and nitrogen, and thus abundances of oxygen, sulfur, and argon in the nebula are expected to be good measures of the levels of those elements in the nascent progenitor star. In particular, type II planetary nebulae (Peimbert 1978) have progenitors of small enough mass that oxygen is not expected to have been altered by CNO processing, yet they are disk objects, based upon their kinematics. Finally, the study of old supernova remnants by Fesen et al. measured abundances in disk objects over a radial range similar to that of Shaver et al.
Figure 1 plots O/H versus galactocentric distance in kiloparcsecs by author, where 12 + log(O/H) is used to represent oxygen. 1 Representative error bars are shown in the lower left panel. Solid lines show first-order least-squares fits for which the fitting parameters are given in Table 2, with the gradient G expressed in dex kpc-1, the absolute abundance A8.5 given as 12 + log(O/H) at the solar circle (8.5 kpc), and c the correlation coefficient. Dot-dashed lines show the composite fit from Table 2 for reference. Note that reported upper and lower limits on abundance ratios were generally not used in our compilation. We also point out that the larger scatter in the Simpson et al. data is probably due in large part to inferring O/H from O+2/S+2 observations plus an assumption of a constant S/O ratio, while the scatter in the Fesen et al. results for supernova remnants may be due to their using abundance-line strength diagnostic diagrams taken from shock models in the literature for estimating abundances.
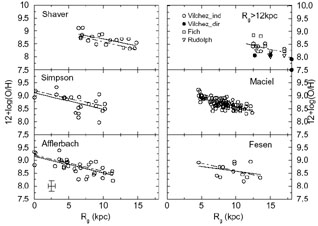 |
Figure 1. 12 + log(O/H) vs. galactocentric distance in kiloparsecs for the several emission-line studies of the Milky Way. First author of each study is given in each panel, where references are given in Table 1. Solid lines are least-square fits to the points, while dot-dashed lines show the composite fit for comparison. Parameters for the fits are given in Table 2. Typical uncertainties for all the data sets are shown with error bars in the bottom left corner. Note that Vílchez & Esteban (1996) employed two methods for obtaining abundances. See their paper for an explanation. |
| Author | G(dex/kpc) | A8.5 | c |
| Shaver | -0.05 ± 0.01 | 8.77 ± 0.14 | -0.69 |
| Simpson | -0.06 ± 0.02 | 8.57 ± 0.15 | -0.56 |
| Afflerbach | -0.06 ± 0.01 | 8.61 ± 0.09 | -0.66 |
| Maciel | -0.07 ± 0.01 | 8.66 ± 0.06 | -0.70 |
| Fesen | -0.04 ± 0.03 | 8.63 ± 0.32 | -0.31 |
| Composite | -0.06 ± 0.01 | 8.68 ± 0.05 | -0.63 |
Combining several data sets allows a visual comparison to be made among them as well as a test of the robustness of the trend exhibited by a single set. Figure 2 shows 12 + log(O/H) versus galactocentric distance in kiloparsecs for the nebular data sets of Shaver et al., Afflerbach et al., Maciel & Köppen, Vílchez & Esteban, Fich & Silkey, Rudolph et al., and Fesen et al. We also present the B-star results from Smartt & Rolleston (1997; filled circles) and Gummersbach et al. (1998; open circles). The Sun's position (Grevesse & Noels 1993) is indicated with a cross, while the error bars in the lower left show typical observational uncertainties for all of the data. A monotonic decrease in oxygen abundance with Galactocentric distance is clearly present in the Milky Way disk. A simple least-squares fit to all points except the B stars indicates a slope of -0.06(± 0.01), A8.5 of 8.68(± 0.05), and a correlation coefficient of -0.63. The data from Afflerbach et al. and Vílchez & Esteban extend the trend of the main body of data toward the Galactic center and anticenter, respectively. The uncertainty of ± 0.2 dex in oxygen abundance is consistent with observational uncertainty, and thus there is no indication of real abundance scatter at a constant radial distance, in accord with findings of Kennicutt & Garnett (1996) in their study of M101.
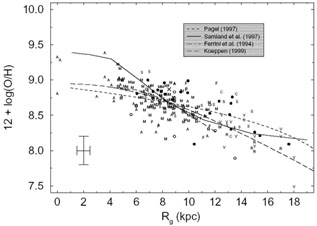 |
Figure 2. 12 + log(O/H) vs. galactocentric distance in kiloparsecs for the data sets of Afflerbach et al. (1997; "A"), Fesen et al. (1985; "F"), Fich & Silkey (1991; "C"), Maciel & Köppen (1994; "M"), Rudolph et al. (1997; "R"), Shaver et al. (1983; "S"), and Vílchez & Esteban (1996; "V"). Filled and open circles are for B-star data from Smartt & Rolleston (1997) and Gummersbach et al. (1998), respectively. Typical uncertainties for all the data sets are indicated in the bottom left corner. Lines represent models by Pagel (1997; dashed line), Samland et al. (1997; solid line), Ferrini et al. (1994; dot-dashed line), and Köppen (1994 and private communication; long-dashed line). The Sun's position is indicated with a cross. |
Several additional points are illustrated in Figure 2. First, notice that the B-star oxygen abundance trend is not noticeably different from the one defined by nebular data; in fact their gradients are very similar to the nebular results. This represents a major development, as previous attempts to infer the disk O/H distribution from B stars (Gehren et al. 1985; Fitzsimmons, Dufton, & Rolleston 1992; Kilian-Montenbruck, Gehren, & Nissen 1994; Kaufer et al. 1994) indicated the absence of a gradient. Smartt & Rolleston speculate that sample size was the culprit in obscuring the gradient in most of the previous studies.
Next, the oxygen abundance distribution implied by planetary nebulae is indistinguishable from the one from H II regions. This would seem to confirm the value of PNe to trace disk metallicity and at the same time perhaps reduce the concern about diffusion (Wielen, Fuchs, & Dettbarn 1996), i.e., that the positions of PN progenitors shift radially during their lives, and thus PN abundances do not represent interstellar matter (ISM) conditions at their present galactocentric distances.
An interesting wrinkle in the MWG metallicity gradient picture is the possibility that the gradient flattens beyond 10 kpc. Results for the three anticenter studies are presented in a single panel in Figure 1. Vílchez & Esteban conclude that their data support the presence of a flattened oxygen gradient in the outer Galaxy, although results from Fich & Silkey and Rudolph et al. neither support nor counter this claim. Recently, Maciel & Quireza (1999) have expanded and updated their sample to include PNe with larger galactocentric distances than those presented here. Like Vílchez & Esteban above, they find evidence for a gradient which flattens beyond 12 kpc. A flattened gradient is both a controversial and interesting conjecture and is tied to the dynamics and mass distributions in the disk (Zaritsky 1992; Mollá, Ferrini, & Diaz 1996; Samland, Hensler, & Theis 1997), and we briefly return to this point in Section 2.1.3 in our general discussion of spiral abundance gradients.
Finally, we have plotted predictions of four chemical evolution models of the present-day disk for comparison with the data. The dashed line shows an analytical result based on the "simple model" from Pagel (1997, eq. [8.14]), while detailed numerical model results are shown from Samland et al. (1997; solid line), Ferrini et al. (1994; dot-dashed line), and Köppen (1994; long-dashed line), where Köppen (1999, private communication) employed a quadratic star formation law but recalculated his model for a radial flow velocity of 0.3 km s-1. 2 All models are scaled so as to match our composite interstellar oxygen abundance of 8.68 at the solar circle (see Table 2). Note that the Samland et al. model predicts a gradient flattening outward from around 11 kpc, the result of (according to them) mass loss of long-living metal-poor intermediate-mass stars and additional infall of low-metallicity gas in equilibrium with metal enrichment from condensation of the intercloud medium.
1 H II region
distances in Shaver et al.'s data have been recomputed using their
reported radial velocities and longitudes, eq. (9.3) in
Binney & Merrifield
(1998),
and assumptions that
R = 8.5
kpc and the average circular velocity is 240 km s-1 across
the relevant portion of the disk.
= 8.5
kpc and the average circular velocity is 240 km s-1 across
the relevant portion of the disk.
2 The unpublished Köppen model also assumes a disk age of 15 Gyr along with exponentially decreasing infall both in time (5 Gyr scale) and galactocentric distance (4 kpc scale). Back.
2.1.2. Metallicity Gradients in External Galaxies
Results from numerous surveys of spiral galaxy abundance patterns show clearly that most spiral disks possess negative gradients qualitatively similar to the one in the Milky Way. Large surveys of O/H in extragalactic H II regions include those of McCall (1982; 40 galaxies; see also McCall, Rybski, & Shields 1985), Vila-Costas & Edmunds (1992; 32 galaxies), and Zaritsky et al. (1994; 39 galaxies). We can add to those the recent studies by Ferguson, Gallagher, & Wyse (1998) and van Zee et al. (1998), both of which explored the outer regions of spirals, where star formation rates are much lower and the regions are less advanced chemically. Vila-Costas & Edmunds reprocess reduced line strengths from the literature to obtain their abundances, while the other authors use primarily their own data for their studies. All these studies are based on optical spectra.
As an example of abundance patterns in two external spirals, in Figure 3 we present a comparison of results for NGC 628 and M33 from Zaritsky et al. (1994) with Milky Way data from Shaver et al. (1983), Afflerbach et al. (1997), and Vílchez & Esteban (1996), where 12 + log(O/H) is plotted against galactocentric distance. The latter quantity has been normalized to the respective galaxy's isophotal radius R0 3 to account for size variations among galaxies; R0 for the Milky Way disk was taken from de Vaucouleurs & Pence (1978). Gradient slopes determined from least-squares fits are given in the figure legend. The two external galaxies clearly resemble the Milky Way in possessing negative abundance gradients.
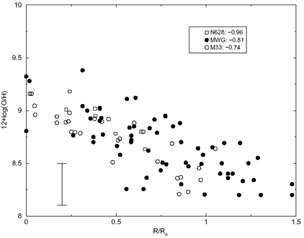 |
Figure 3. 12 + log(O/H) vs. galactocentric distance in units of isophotal radius for the Milky Way (filled circles), M33 (open circles), and NGC 628 (open squares). Data sources are given in the text, while gradient slopes in dex R0-1 are given in the legend. |
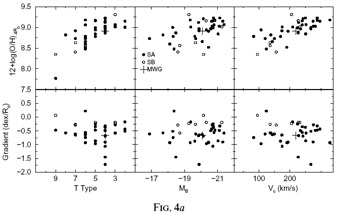
A much larger collection of abundance plots for individual spirals can be found in Zaritsky et al. (1994). We have extracted results from that paper and plotted them in Figure 4a, where characteristic abundances 4 (top panels) and gradient slopes in dex R0-1 (bottom panels) are shown as functions of galaxy morphological type (T type), absolute blue magnitude MB, and maximum circular velocity Vc in km s-1. All three of these parameters track galaxy mass, where smaller T-type indices, more luminous integrated blue magnitudes, and larger rotational velocities generally correspond with more massive spirals. Normal (SA) and barred (SB) spirals are shown separately using filled and open symbols, respectively. Abundance parameters for the Milky Way composite fit from Table 2 are indicated in Figure 4a with plus symbols, where we have adopted T = 4, MB = -20.08, and R0 = 11.5 kpc (de Vaucouleurs & Pence 1978), along with Vc = 220 km s-1 (Kochanek 1996).
 |
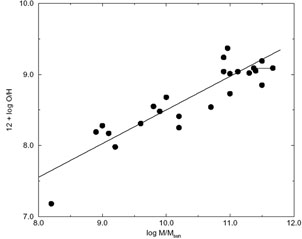 |
Figure 4. (a) Characteristic abundances (top three panels) and gradient slopes (bottom three panels) from Zaritsky et al. (1994) plotted against morphological T type, absolute blue magnitude MB, and circular velocity Vc in km s-1. Regular and barred spirals are shown with filled and open circles, respectively. Milky Way data (see text for references) are shown with plus symbols. (b) Oxygen abundance at one effective radius expressed as 12 + log(O/H) vs. log(galaxy mass) in solar units for a small sample of spirals. Abundance data are from Garnett & Shields (1987), Skillman et al. (1996), and Henry et al. (1996). Sources for galaxy masses are given in Henry et al. The two points connected by a line are for NGC 753, whose mass was determined for H0 values of 50 and 100 km s-1. |
Two important points are implied by Figure 4a: (1) Characteristic abundances increase with galaxy mass, while gradient slopes are uncorrelated with this parameter; and (2) Characteristic abundances in normal and barred spirals are indistinguishable, but barred spirals appear to have flatter (less negative) gradients. Both of these results have been noted previously. Garnett & Shields (1987) plotted characteristic O/H values against galaxy mass for numerous spirals and found a direct correlation between these two parameters, while Pagel et al. (1979) first suggested that barred spirals may have flatter gradients, a pattern clearly borne out in the more extensive work by Martin & Roy (1994), who relate gradient slope to bar strength, a quantity which measures bar ellipticity. Martin & Roy find direct relations between the slope of the oxygen abundance gradient of a barred spiral and the galaxy's bar strength (ellipticity) and length in the sense that stronger bars are accompanied by flatter gradients. This empirical result is consistent with radial flow models of chemical evolution in which the presence of a bar enhances large-scale mixing over the galaxy's disk, damping radial abundance variations.
Interestingly, if gradient slope in dex kpc-1 (as opposed to dex R0-1 shown here) is plotted versus MB (see Garnett 1998), a correlation appears such that more luminous galaxies have flatter slopes. The dependence of slope behavior on normalization is no doubt related to the fact that R0 for luminous galaxies tends to be longer in kiloparsecs. Since the vertical scatter in the lower panel of Figure 4a is comparable to observational uncertainties, this may imply a universal gradient in dex R0-1, which in turn could be associated with similar timescales for viscous angular momentum transport and star formation, producing exponential gradients in surface density and abundances (Lin & Pringle 1987; Yoshii & Sommer-Larsen 1989).
We illustrate explicitly the correlation between galaxy mass and characteristic abundance in Figure 4b, where we plot 12 + log(O/H) at one effective radius versus the log of the galaxy mass in solar units for a sample of spiral galaxies. Abundance data are from Garnett & Shields (1987), Skillman et al. (1996), and Henry et al. (1996). Sources for galaxy masses, which for the most part are inferred from rotation curves, are given in Henry et al. The two points connected by a horizontal line are for NGC 753, whose mass was determined for H0 values of 50 and 100 km s-1. The least-squares fit to the data, shown with a solid line, indicates that 12 + log(O/H) = 3.79 + 0.47 × log M, where M is in solar masses. Note that this relation ignores the low surface brightness spirals (McGaugh 1994) which appear to have low metallicity but high mass. These objects are discussed briefly in Section 2.1.3.
Finally, Figure 5 shows the observed relation
between 12 + log(O/H) and total (disk+bulge) surface density,
 , in
M
, in
M pc-2 at the corresponding location from
Vila-Costas & Edmunds
(1992;
their Fig. 7d), where open and closed squares represent H II regions residing in late (Scd-Irr) and early
(Sab-Sc) spirals, respectively. Vila-Costas & Edmunds assumed that
the mass distribution follows the light distribution and employed a
constant mass-to-light ratio for each galaxy, the latter determined from
a rotation curve (see Vila-Costas & Edmunds and
McCall 1982
for details). The scatter is consistent with observational uncertainty,
and thus we see a clear positive correlation between abundance and local
surface density in spirals, with earlier spirals generally possessing
higher abundances per unit surface density.
pc-2 at the corresponding location from
Vila-Costas & Edmunds
(1992;
their Fig. 7d), where open and closed squares represent H II regions residing in late (Scd-Irr) and early
(Sab-Sc) spirals, respectively. Vila-Costas & Edmunds assumed that
the mass distribution follows the light distribution and employed a
constant mass-to-light ratio for each galaxy, the latter determined from
a rotation curve (see Vila-Costas & Edmunds and
McCall 1982
for details). The scatter is consistent with observational uncertainty,
and thus we see a clear positive correlation between abundance and local
surface density in spirals, with earlier spirals generally possessing
higher abundances per unit surface density.
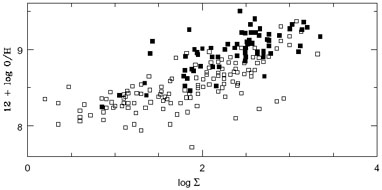 |
Figure 5. 12 +
log(O/H) of extragalactic H II regions vs. the
logarithm of the total surface density
|
3 The isophotal radius
R0 is the radial distance from
the galactic nucleus at which the declining disk surface brightness
reaches 25 mag arcsec-2. Comparisons of data among galaxies
are made most frequently using the isophotal radius, but one could also
use the effective radius, i.e., the radius of an aperture admitting
one-half of the light from the disk, or kiloparsecs. To add to the
confusion, literature sources for (nonnebular) bulge or elliptical
galaxy abundances usually express gradients as
 log Z /
log Z /
 log R! This
last notation gives nonsensical abundances at the nucleus of a galaxy,
but seems to match observed profiles out to the observational limit,
which is usually far short of the isophotal radius for integrated
starlight spectroscopy.
Back.
log R! This
last notation gives nonsensical abundances at the nucleus of a galaxy,
but seems to match observed profiles out to the observational limit,
which is usually far short of the isophotal radius for integrated
starlight spectroscopy.
Back.
4 The characteristic abundance is the abundance at 0.4R0 as determined by a least-squares fit to the data. See Zaritsky et al. (1994). Back.
2.1.3. Assorted Issues about Galaxy Metallicity
Other issues concerning abundance gradients include questions about gradients perpendicular to the disk as well as azimuthal distributions, abundance patterns in low surface brightness galaxies, effects of cluster environment on gradients, the mathematical form of abundance profiles, and results of extragalactic planetary nebula studies. We treat these topics briefly.
A negative vertical gradient in O/H in the Milky Way is suggested by planetary nebula studies. Abundance data compiled by Kaler (1980) for PNe ranging in height above the disk from less than 0.4 kpc to greater than 1 kpc show a decrease in O/H with increasing height above the plane. A comparison of more recent studies of PNe close to the plane (Perinotto 1991), greater than 300 pc above the plane (Cuisinier, Acker, & Köppen 1996), and in the halo (Howard, Henry, & McCartney 1997) shows averages of 12 + log(O/H) for these three samples of 8.68, 8.52, and 8.02, respectively, qualitatively consistent with Kaler.
Thorough tests for azimuthal gradients in spiral disks have yet to be carried out. One example of apparent O/H asymmetry is discussed by Kennicutt & Garnett (1996) in their study of M101. They find that H II regions located along a spiral arm southeast of the major axis have a lower oxygen abundance by 0.2-0.4 dex compared with H II regions on the opposite side.
Global metallicities in low surface brightness galaxies are generally found to be subsolar by roughly a factor of 3, according to McGaugh (1994), indicating that these galaxies evolve very slowly and form few stars during a Hubble time. Apparently, they also lack detectable gradients. This, despite the fact that these objects are similar in mass and size to prominent spirals defining the Hubble sequence. McGaugh suggests that a galaxy's environment and surface mass density are more relevant to galaxy evolution than gross size.
Effects of cluster environment on the chemical evolution of galaxies have been investigated by Skillman et al. (1996), who studied oxygen profiles in several Virgo spirals representing a range in H I deficiency (taken as a gauge of cluster environmental interactions). Their results imply that global metal abundances in disks tend to be higher in stripped galaxies, presumably because reduced infall of metal-poor H I gas means less dilution of disk material. Henry et al. (1996 and references therein) investigated metallicity and heavy-element abundance ratios (N/O, S/O) in three cluster spiral disks with normal H I and found no clear signatures of environmental effects. Thus, cluster environment alone is apparently not a sufficient condition for altered chemical evolution.
The mathematical form of abundance profiles in spiral disks has been investigated recently by Henry & Howard (1995), who fit line strength behavior over the disks of M33, M81, and M101 using photoionization models. Their best fits for O/H versus galactocentric distance were produced using exponential profiles, although power law forms could not be ruled out. However, linear profiles poorly reproduced the observations. Henry & Howard also concluded that, despite some observational and theoretical claims to the contrary (see Mollá et al. 1996), it is premature to conclude that gradient flattening is present in the outer parts of some disks.
Planetary nebulae have been used as probes of interstellar abundances in a small number of external galaxies. A recent paper by Jacoby & Ciardullo (1999) presents abundances for 12 bulge and three disk planetaries in M31. Their bulge objects have oxygen abundances whose average is similar to the value observed in the Large Magellanic Cloud. Interestingly, the implied bulge metallicity is significantly below the level expected from observations of [Fe/H]. In another study, Stasinska, Richer, & McCall (1998) determine abundances of oxygen, neon, and nitrogen in planetaries in the bulges of the Milky Way and M31, M32, and the Magellanic Clouds. These authors find higher oxygen levels in the Milky Way and M31 bulges than in the Clouds, and also reconfirm the tight correlation between neon and oxygen discussed below in Section 2.2.3.
2.1.4. Summary Thoughts about Spiral Metallicities
A detailed synthesis based upon the observations is beyond the scope of our review. However, the following would seem to provide a reasonable set of explanations.
There appear to be two fundamental physical parameters for a galaxy which influence its abundance characteristics. These are total mass and the distribution of material as a function of galactocentric distance. As supernovae erupt, their metal-rich ejecta are more likely retained in systems with greater mass. Thus, the more massive galaxies might be expected to exhibit higher global metallicities, which in fact they do. Furthermore, observations indicate that metallicities tend to be greater in regions where the total surface density is higher, perhaps because the star formation process is sensitive to the local density and so more metals are produced in locations with high densities. Since matter in spirals tends to form an exponential disk (Binney & Merrifield 1998) with surface density falling off with greater galactocentric distance, we might then expect metallicity locally in the disk to track this pattern.