ABUNDANCES FROM STELLAR SPECTRA
We do not wish to include a complete description of stellar atmospheres in this review as most readers have completed a stellar atmospheres course or have textbooks like Mihalas (1978) on their shelves or have read shorter introductions like chapter 12 of Cowley (1995). However, in the interest of keeping up to date, we provide a brief description with emphasis on oft-heard buzzwords. Converting measured absorption feature strengths into abundances requires a model stellar atmosphere that gives the run of physical variables like temperature and pressure with optical depth. With today's fast computers, it is no longer much of a computational burden to compute fairly realistic LTE model atmospheres, most of which have the following features. (1) Plane-parallel geometry. This is a good approximation for most stars, but a spherical geometry is needed for M giants and other stars that have extended envelopes. (2) A modern model atmosphere (see, e.g., Gustafsson 1989; Kurucz 1993) will be line-blanketed. That is, individual transitions from (usually millions) of atomic and molecular lines are explicitly included in the frequency-dependent opacity calculations along with the various sources of continuous opacity like electron scattering or H-. (3) Convection is often treated in the mixing length approximation, but alternatives are always being tested. (4) For many stars, local thermodynamic equilibrium (LTE) is assumed. In this case the local radiation field and the local thermodynamic state (which can be described by temperature and pressure alone) of the matter are equilibrated. The alternative is non-LTE (NLTE), in which the radiation field decouples from the matter. The complicating part of this is that atomic level occupation numbers then depend mostly on the radiation field rather than the local matter thermodynamics, and the radiation field is not local and therefore a global self-consistent solution must be sought. Extreme NLTE prevails in the case of nebulae and hot stars, while most stars can be treated with the LTE assumption for most lines. However, a temperature inversion above the photosphere (i.e., a chromosphere) will introduce certain NLTE effects in some lines. If these lines are going to be used for abundance analysis, they need to be treated appropriately. See Mihalas (1978) or Kudritzki & Hummer (1990) for a description of NLTE methods in hot stars.
Except for those stars where spherical geometry effects become important, effective temperature Teff, surface gravity log g (where g is expressed in cm s-2), and abundance are sufficient parameters to begin the calculation of a model star. Temperatures can be gotten from calibrations of broadband or narrowband colors, by Balmer line strength, or by consideration of two or more ionization states of the same species (by requiring consistent abundance results from all ionization states). Abundance analysis is often not very sensitive to surface gravity.
There is also the matter of Doppler broadening of lines. Thermal motion
of gas particles causes a broadening of the line profile that is almost
always larger than the width of the line as broadened by pressure and by
radiation damping. In the LTE approximation inclusion of this effect is
trivially accomplished by convolving the intrinsic Lorentzian line
profile with the Gaussian thermal Doppler profile. But there is also the
matter of bulk motions in the atmosphere, in the Sun seen as
prominences, spicules, granules, acoustical waves, and other
phenomena. These add Doppler width to lines, but their velocity
distribution is not known. In the face of the total unknown, we follow
historical precedent and assume Gaussian random motion, and an
empirically adjusted term is added to the width of the Gaussian Doppler
profile. That is, inside the Gaussian broadening function
e-(
/ D),
 |
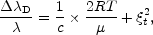(B1) |
where is the central
wavelength of the line,
D is the
Doppler width, R is the gas constant, T is the
temperature, µ is the mean atomic weight, c is the
light speed, and
t is
called the microturbulent velocity, meant to account for
Gaussian-random, optically thin turbulent motion in the atmosphere. The
final Doppler motion to be considered is macroturbulence, very
large moving elements that can be considered independent
atmospheres. Such motions will not change the equivalent widths of
absorption lines, but they will change the line profile.
Atomic (or molecular) parameters are often crucial to a reliable abundance. Parameters may include damping constants for radiation and van der Waals forces. The damped line profile is usually approximated by a Lorentzian function. The atomic parameters that are mentioned most often are the "gf-values," where g is the statistical weight of the level and f is the oscillator strength; they are usually combined as "log gf." The gf-values can be calculated with varying degrees of accuracy, and many can be measured in the laboratory, but the usual method of getting accurate values is to compute a model atmosphere for the Sun. The equivalent widths of the line transitions one is interested in studying are measured from the solar atlas, and also computed from the model atmosphere using standard meteoritic+photospheric abundances, for example those of Grevesse et al. (1996). The gf-values are then adjusted until the model equivalent widths match those of the Sun. This method begins to fail for stars too dissimilar from the Sun in temperature because the line of interest will be invisible in one of the two stars or on a different part of the curve of growth.
The curve of growth is the increase in equivalent width of a line as a function of abundance. When lines are weak, they grow linearly with the abundance. When the line center nears its maximum depth, little growth in equivalent width is seen until the line is so saturated that the weak wings of the line profile contribute. Thus the textbook curve of growth has a linear-with-abundance portion, an almost flat portion, and then a proportional-to-the-square-root-of-the-abundance portion. For accurate abundance work, it is therefore advantageous to choose weak lines in the linear-growth part of the curve.
Observational material for spectroscopic abundance work will vary
according to circumstance. In the ideal case, one would have high-S/N,
high-resolution (R =
/
= 50,000-100,000) spectra
compared with near-perfect models. In reality, the models have defects
and many/most of the interesting stars are too far away for both
high-S/N and high-resolution spectra. The usual solution is to go to
lower resolution. The ultimate low-resolution spectrum is broadband
photometry (R ~ 10), which can be coaxed to yield good
information about Z with suitable assumptions and calibrations,
but little information about individual elements. A resolution at which
some elemental abundance information becomes available is about R
~ 500, but only for the strongest, cleanest absorption features. This
is the approximate resolution needed for integrated starlight studies.