


Relative motion in the line of sight shifts the lines in the spectrum of any light-source. If a luminous body is rushing towards the observer, the light-waves are crowded on to one another, and are all shortened. Consequently, the entire pattern of spectral lines is displaced from its normal position, in the direction of the violet end of the spectrum-towards the shorter waves. On the other hand, if the light-source is rapidly receding from the observer, the light-waves are dragged out and lengthened, and the pattern of the spectrum is shifted towards the red.
In both cases, whether the shift
d is to the red or
to the violet, the fractional displacement
d
is to the red or
to the violet, the fractional displacement
d /
/
 is
constant throughout a given spectrum. Each line is shifted
by a constant fraction of its normal wave-length. Thus
the fraction describes and measures the motion in the
line of sight, the `radial velocity' as it is called. Actually,
the velocity of the light-source v is merely the velocity
of light c multiplied by the fractional velocity-shift,
1
is
constant throughout a given spectrum. Each line is shifted
by a constant fraction of its normal wave-length. Thus
the fraction describes and measures the motion in the
line of sight, the `radial velocity' as it is called. Actually,
the velocity of the light-source v is merely the velocity
of light c multiplied by the fractional velocity-shift,
1
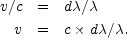 |
For instance, a shift of 0.00001, or one part in a hundred thousand, represents a velocity of 1.86 miles per second; a shift of 0.001, or one-tenth of 1 per cent., a velocity of 186 miles per second.
Velocity-shifts of these dimensions, both to the violet and to the red (approaching and receding), are well known in the laboratory, and among the planets and the stars; their study, in fact, is an essential part of the investigation of stellar motions. And occasionally, in the tremendous explosions we observe as novae, masses of gas are driven away from a star at even. greater velocities; violet-shifts have been recorded as. large as 1 per cent., representing velocities of approach as high as 1,860 miles per second. Thus velocity-shifts, on a microscopic scale, are familiar phenomena, and their interpretation is not to be questioned.
Now the red-shifts observed in nebular spectra behave as velocity-shifts
behave - the fractional shift
d /
/
 is constant
throughout a given spectrum - and
they are readily expressed as velocities of recession.
The scale is so convenient that it is widely used, even
by those cautious observers who prefer to speak of
`apparent velocities' rather than actual motion. For
instance, the law of red-shifts is frequently called the
'velocity-distance relation'.
is constant
throughout a given spectrum - and
they are readily expressed as velocities of recession.
The scale is so convenient that it is widely used, even
by those cautious observers who prefer to speak of
`apparent velocities' rather than actual motion. For
instance, the law of red-shifts is frequently called the
'velocity-distance relation'.
When Slipher, in his great pioneering work, assembled the first considerable lists of red-shifts, the observations were necessarily restricted to the brighter, nearer nebulae. Consequently, the shifts were moderately small (less than 1 per cent.), and they were accepted without question as the familiar velocity-shifts. Attempts were immediately made to study the motions of the nebulae by the same methods used in the study of stellar motions. But later, after the 'velocity-distance relation' had been formulated, and Humason's observations of faint nebulae began to accumulate, the earlier, complete certainty of the interpretation began to fade.
The disturbing features were the, facts that the 'velocities' reached enormous values and were precisely correlated with distance. Each million light-years of distance added a hundred miles per second to the `velocity'. As Humason swept farther and farther out into space he reported `velocities' of 5,000 miles per second, then 10,000 then 15,000. Finally, near the absolute limit of his spectrograph he recorded red-shifts of 13 and 14 per cent., `velocities' of about 25,000 miles per second - around the earth in a second, out to the moon in 10 seconds, out to the sun in just over an hour. Red-shifts continue to increase beyond the range of the spectrograph, and, for the faintest nebulae that can be photographed, they are presumably about double the largest recorded shifts - the `velocities' are about 50,000 miles per second. These quantities we are asked to accept as measuring a general recession of the nebulae, an expansion of the universe itself. The law of red-shifts then reads: the nebulae are receding from the earth, in all directions, with velocities that are proportional to their distances from the earth.
1 The relation v / c =
d /
/
 is a first approximation
which serves well.
enough for small shifts. The rigorous expression, derived from the
theory of relativity, is complicated and departs more and more from
the simple relation as the shifts increase.
Back.
is a first approximation
which serves well.
enough for small shifts. The rigorous expression, derived from the
theory of relativity, is complicated and departs more and more from
the simple relation as the shifts increase.
Back.