Spatial Curvature

The departures from uniformity are positive; the numbers of nebulae increase faster than the volume of space through which they are scattered. Thus the density of the nebular distribution increases outwards, symmetrically in all directions, leaving the observer in a unique position. Such a favoured position, of course, is intolerable; moreover, it represents a discrepancy with the theory, because the theory postulates homogeneity. Therefore, in order to restore homogeneity, and to escape the horror of a unique position, the departures from uniformity, which are introduced by the recession factors, must be compensated by the second term representing effects of spatial curvature.

There seems to be no other escape. Observations demonstrate that

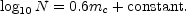Relativistic cosmology requires that

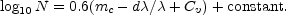Therefore,

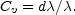The curvature of space is demonstrated and measured by the postulated recession of the nebulae. To the observer the procedure seems artificial. He has counted the nebulae to various limits, applied only the corrections that are necessarily required (energy-corrections), and derived the quite plausible result of uniform distribution. Now, in testing the relativistic theory, he introduces a new postulate, namely, recession of the nebulae, and it leads to discrepancies. Therefore, he adds still another postulate, namely, spatial curvature, in order to compensate the discrepancies introduced by the first. The accumulation of assumptions is uneconomical, and the justification must be sought in the general background of knowledge. The outstanding argument is the fact that velocity-shifts remain the only permissible interpretation of red-shifts that is known at the present time.

Well, perhaps the interpretation is correct and we do inhabit a rapidly expanding universe. In that case the surveys indicate the nature and amount of the spatial curvature. It must be such that the effects on the nebular distribution are just equal to the recession factors at the limits of the various surveys: Actually, no curvature can be found which exactly compensates for the apparent departures from uniformity in each of the surveys. Nevertheless, if we admit the presence of rather considerable systematic errors in the observations, it is possible to select a curvature which will more or less restore the homogeneity. Hidden errors of the necessary dimensions are by no means impossible in the very delicate investigations near the limits of a great telescope. ⁶ They may be improbable, but they are not impossible. Therefore, the expanding universe can be saved by introducing a sufficient amount of spatial curvature. The plausible values are narrowly limited, and they indicate a radius of curvature that is positive and comparatively small. In fact the radius, about 470 million light-years, is a trifle less than the range of the 100-inch reflector for normal nebulae. Thus the second of the three arbitrary elements in the description of the relativistic universe is determined. If the universe is expanding, the spatial curvature is real and positive.

The nature of the curvature has rather grave implications. Since the curvature is positive, the universe is closed. Space is closed as the surface of a sphere is closed. The universe has a definite, finite volume although it has no boundaries in three-dimensional space. The remarkably small numerical value of the radius of curvature is a complete surprise. It implies that a large fraction of the universe, perhaps a quarter, can be explored with existing telescopes. ⁷ The small volume of the universe is another strange and dubious conclusion. The familiar interpretation of red-shifts as velocity-shifts very seriously restricts not only the time scale, the age of the universe, but the spatial dimensions as well. On the other hand, the alternative possible interpretation, that red-shifts are not velocity-shifts, avoids both difficulties, and presents the observable region as an insignificant sample of a universe that extends indefinitely in space and in time.

⁶ A systematic error of the order of 0.35 mag., in the limiting magnitudes of the surveys, as compared with the magnitudes of the nebulae used in the formulation of the law of red-shifts, would be required in order to fully satisfy the relation C_v = d / . Back.

⁷ The volume of this universe would be 2² R³, where R is the radius of curvature, or about 2 × 10²⁷ cubic light-years. The universe would contain about 400 million nebulae. Back.