12.5.1. Synchrotron Radiation

A single electron of energy E spiraling in a magnetic field at ultra-relativistic velocities [(1 - v² / c²) << 1] has its radiation concentrated in a cone of half angle ~ E / mc². An observer sees a short burst of emission lasting only during the time, t, that the cone is pointed toward the observer. The radiation is concentrated in the high-order harmonics, = (E / mc²)², of the classical gyrofrequency _g = e B / m. The frequency distribution of the radiation is given by a complex expression conveniently represented by

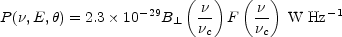(12.4)

where

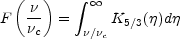and where B = B sin is the component of the magnetic field perpendicular to the line of sight; K_5/3() is a modified Bessel function; is the angle between the electron trajectory and the magnetic field (pitch angle) ; and the critical frequency _c is given by

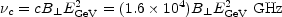(12.5)

The spectrum of the observed radiation depends on the angle between the line of sight and the electron trajectory and on the plane of polarization. In the remainder of this chapter the supbscript "" is dropped and the symbol B is understood to represent the perpendicular component of the magnetic field.

The total power radiated by each electron is given by

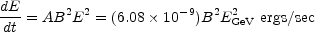(12.6)

where A = 6.08 × 10^-9 and c = 1.6 × 10⁷.

The distribution given by equation (12.4) has a broad peak near ~ 0.28_c. For ( / _c) < 0.3, P() ^1/3. For ( / _c) > 0.3, P() ( / _c)^1/2 e^{- / _c} and the radiation falls off rapidly with increasing frequency.

For an assembly of electrons with a number density N(E)dE between E₁1 and E₂, Equation (12.4) can be integrated to find the total radiation at any frequency from all electrons. Using Equation (12.5) and making a change of variable this becomes

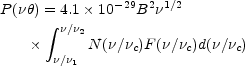(12.7)

where ₁ and ₂ are the critical frequencies defined by Equation (12.6) corresponding to E₁ and E₂.

In the special case where the electron energy distribution is a power law, that is, N(E)dE = K E^- dE, Equation (12.7) becomes

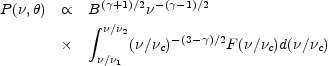(12.8)

For 1 the major contribution to the integral is when ( / _c) ~ 1 so that the limits of integration may be extended from zero to infinity without introducing significant error. The integral is then essentially constant when 3₁ 10₂. The radio spectrum then is a power law,

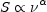(12.9)

with a spectral index = - ( - 1) / 2.

It must be emphasized that this approximation is valid only when 1; and in particular that no form of energy distribution can give a spectrum that rises faster than the low-frequency asymptotic limit of ^1/3 for a single electron.

As described in Section 12.4.3, many sources show nearly power law radio-frequency spectra, with a common spectral index ~ - 0.8 corresponding to an electron energy distribution index, ~ 2.6. Deviations from a constant radio spectral index may be explained as being due to (1) variations in as a function of energy which may exist either in the initial electron energy distribution or occur as a result of differential energy loss in an initial power law distribution; (2) self-absorption in the relativistic electron gas; (3) absorption in a cold HII region between us and the source; (4) the effect of a dispersive medium in which the electrons are radiating.