12.5.9. Interpretation of Time Variations

The observations of time variations provide direct evidence in some sources of repeated energetic events which may provide a nearly continuous input of energy necessary to account for the observed energy requirements of the extended sources.

The form of the observed intensity variations is most simply interpreted in terms of a cloud of relativistic particles which is initially opaque out to short wavelengths, but which, due to expansion, becomes optically thin at successively longer wavelengths. In its simplest form the model assumes that the relativistic particles initially have a power law spectrum, that they are produced in a very short time in a small space, that the subsequent expansion occurs at a constant velocity, and that during the expansion the magnetic flux is conserved. Thus

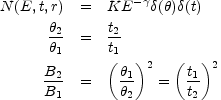(12.40)

where is the angular dimensions, t the elapsed time since the outburst, B the magnetic field, and the subscripts 1 and 2 refer to measurements made at two epochs t_l and t₂. A more detailed mathematical description of the model has been given by van der Laan for the nonrelativistic (1966) and the relativistic (1971) case. The discussion below follows that of Kellermann and Pauliny-Toth (1968).

The observed flux density as a function of frequency, , and time, t, is given by

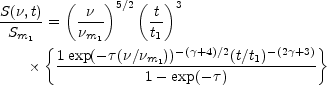(12.41)

where S_m1 is the maximum flux reached at frequency _m1 at time t₁.

If the optical depth is taken as the value of at the frequency, _m, at which the flux density is a maximum, then it is given by the solution of

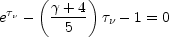(12.42)

The maximum flux density at a given frequency as a function of time occurs, at a different optical depth, _t, given by the solution of

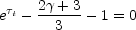(12.43)

In the region of the spectrum where the source is opaque ( >> 1), the flux density increases with time as

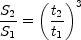(12.44)

Where it is transparent ( << 1), the flux density decreases as

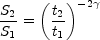(12.45)

The wavelength, _m, at which the intensity is a maximum is given by

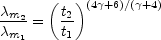(12.46)

and the maximum flux density, S_m, at that wavelength is given by

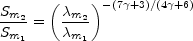(12.47)

In most variable sources the outbursts occur so rapidly that the emissions from different outbursts overlap both in frequency and time, and so a detailed quantitative analysis is difficult. As pointed out by van der Laan (1966), the spectra of individual bursts are cumulative, suggesting spacially separated outbursts. If the different events occur in the same volume of space, the number of relativistic particles would be cumulative, rather than the spectra.

To the extent that it has been possible to separate events in some sources, the individual outbursts seem to follow surprisingly well the simple model of a uniformly expanding cloud of relativistic particles. The data relating S_m, t_m, and _m (Equations 12.46 and 12.47) indicate that the initial value of is in the range 1 to 1.5. This agrees with the spectral index of ~ - 1/4 initially observed in the optically thin region of the spectrum. At least for one year following an outburst the expansion appears to continue at a constant rate, and the value of is unchanged by radiation losses or by inverse Compton scattering at least for < 10 GHz. From Equation (12.15) this places a limit on the magnetic field of B₀ 1 Gauss. From the requirement that T < 10¹² and Equations (12.22) and (12.25), we have B₀ 0.1 Gauss. Thus we conclude that B₀ ~ 1 Gauss and in those sources where there are good data the magnetic flux seems to be approximately conserved, at least during the initial phases of the expansion. But because the data from long-baseline interferometer observations when used in Equation (12.22) indicate that B ~ 10^-4 gauss over a wide range of dimensions for both variable and nonvariable sources, and since this is also the value of the field estimated from minimum energy arguments, it appears that the flux is conserved for only a limited time, after which the relativistic particles diffuse through a fixed magnetic field of about 10^-4 Gauss. In this way many repeated outbursts may provide the particles in the extended sources, although as explained earlier, this presents formidable energy problems unless energy is continuously supplied.

In the case of the variable radio galaxies, whose distance can be determined from their redshift, the initial dimensions appear to be well under one light year and the initial particle energy in a single outburst about 10⁵² ergs. Repeated explosions over a period of 10⁸ years at a rate of one per year are required to account for the minimum total energy in the extended sources, but even this falls short by a factor of about 10⁵ if account is taken of energy lost during the expansion.

The direct measurement of the angular size and expansion rate of variable sources using long-baseline interferometry is now possible, and can be used to determine uniquely the magnetic field (Equation 12.18), and when the distance is known the total energy involved in each outburst (Equations 12.25 and 12.27).

The model of a uniform isotropic homogeneous instantaneously generated sphere of relativistic electrons, which expands with a uniform and constant velocity, where magnetic flux is conserved, and where the only energy loss is due to expansion, is mathematically simple. Clearly, such sources are not expected to exist in the real world, and it is indeed remarkable that the observed variations follow even approximately the predicted variations. A more realistic model must take into account nonconstant expansion rates, the nonconservation of magnetic flux, changes in , the finite acceleration time for the relativistic particles, and the initial finite dimensions. But these are relatively minor modifications, and the observed departures from the predictions of the simple model should not, as is sometimes done, be used to infer that the general class of expanding source models is not relevant to the variable source phenomena. Rather the departures from the simple mathematical model can be used to derive further information about the nature of the source.

In the case of the continued production of relativistic particles, or where the initial volume of the source is not infinitely small, the initial spectrum is not opaque out to very short wavelengths, and the source is always transparent at frequencies higher than some critical frequency, ₀. In the transparent region of the spectrum the flux variations occur simultaneously and reflect only the rate of particle production and/or decay due to synchrotron and inverse Compton radiation.

The experimental determination of ₀ may be used to estimate the initial size of the source. Characteristically ₀ ~ 10 to 30 GHz, corresponding to initial dimensions of about 10^-3 are second for B ~ 1 Gauss. For typical radio sources with 0.1 < z < 1, the initial size derived in this way is from 1 to 10 light years. This is roughly consistent with the direct determination of the angular sizes made by long-baseline interferometry, but it must be emphasized that so far these measurements have not been made in sufficient detail to permit a detailed comparison, or to estimate from Equation (12.21) the initial magnetic field.

In those sources where good data exist in the spectral region > ₀, the observed variations occur simultaneously as expected from the model, and with equal amplitude, indicating an initial spectral index ~ 0, or ~ 1, in good agreement with the value of derived from Equations (12.46) and (12.45).

In the spectral region > ₀, the observed flux variations depend on the total number of relativistic particles, their energy distribu tion, and the magnetic field. Thus observations in this part of the spectrum reflect the rate of generation of relativistic particles more closely than observations in the opaque part of the spectrum.

In some sources ₀ occurs at relatively low frequencies of 1 or 2 GHz. This poses a serious problem, for the following reason. If variations occur on a time scale of the order of , then it is commonly assumed that the dimension of the emitting region, l, is less than c, since otherwise the light travel time from different parts of the source to the observer would "blur" any variations which occur. Using the distance obtained from the redshift, a limit to the angular size, , may be calculated, and from Equation (12.22) an upper limit to the magnetic field strength is obtained.

For a typical quasar, such as 3C 454.3, ~ 1 yr, z ~ 1, 10^-4 arc second, and B 10^-5 Gauss. With such weak fields the energy required in relativistic particles is very high and is 10⁵⁸ ergs, and the repeated generation of such enormous energies in times of the order of one year or less is a formidable problem. Also the limit to the angular size deduced from the light travel time argument often results in a peak brightness temperature which may exceed the expected maximum value of 10¹² K (Equation 12.24). For these reasons it has been questioned by some whether or not in fact the quasars are at the large distances indicated by their redshifts (e.g., Hoyle, Burbidge, and Sargent, 1969), or whether they do indeed radiate by the ordinary synchrotron process.

One way in which the theoretical brightness temperature limit may be exceeded is if the relativistic electrons are radiating co herently. Stimulated emission or negative absorption leading to coherent radiation is possible in opaque synchrotron sources, if the relativistic electrons are moving in a dispersive medium where the index of refraction is less than unity.

However, other than the seemingly excessive brightness temperature implied by some of the variable source observations, the ex panding source model and the ordinary incoherent synchrotron process appear to be adequate to explain all of the observed phenomena.

Another way to explain the rapid variations was pointed out by Rees (1967), who showed that if the source is expanding at a velocity v ~ c, then the differential light travel time between the approaching and receding parts of the source can cause the illusion of an angular expansion rate corresponding to an apparent linear velocity v > c. In this case the angular size and peak brightness temperature are larger than suggested by the observations; and from Equation (12.36), which depends on a high power of , the required particle energy is greatly reduced. However, there is a limit to the extent that the total energy requirements can be reduced by this "super-light" expansion theory, since as the particle energy is decreased when is increased, the magnetic energy is increased. The minimum value of the total energy occurs when the two are approximately equal, and for the typical quasar it is ~ 10⁵⁵ ergs (e.g., van der Laan, 1971).

Unfortunately, the variation in total intensity for the relativistically expanding source is very similar to that for the nonrela tivistic model, so that they cannot be easily distinguished merely from observations of the intensity variations. The direct observations of the variations in angular size likewise do not distinguish between "superlight" velocities at cosmological distances and nonrelativistic velocities in a "local" model for quasars.

An interesting variation on the expanding source model has been suggested by the Russian astrophysicists Ozernoy and Sazonov (1969), who propose that two or more discrete components are "flying apart" at relativistic velocities, while at the same time expanding. Evidence for relativistic component velocities has been obtained from long-baseline interferometer observations, but with the meager data so far available it has not been possible to uniquely distinguish between actual component motions and properly phased intensity variations in stationary components.

It may be expected, however, that future observations of intensity variations as a function of wavelength, when combined with the direct observation of the variations in angular size, not only will uniquely determine the dynamics and energetics of the radio outbursts, but also will specify the initial conditions of the outburst with sufficient accuracy to limit the range of theoretical speculation concerning the source of energy and its conversion to relativistic particles. In particular, there must be increased emphasis on observations made at the shortest possible wavelengths, since these most nearly reflect the conditions during the time just following the outburst (Equation 12.44).