13.1.4. Energy Considerations

The problem of the origin and evolution of extragalactic radio sources is a formidable one; in particular, the source of energy needed to account for the large power output and the manner in which this energy is converted to relativistic particles and magnetic flux is a subject of considerable debate. Assuming only that synchrotron radiation from ultra-relativistic electrons is responsible for the observed radiation, the necessary energy requirements were shown by Burbidge (1958) to be as much as 10⁶⁰ ergs or more.

Following Burbidge, if the relativistic particles have a power law distribution with an index p between E_l and E₂, then for p 2, the energy contained in relativistic electrons is

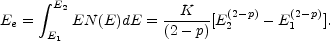(13.4)

The constant K can be evaluated if the distance to the source is known. The total luminosity, L, is given by integrating Equation (1.10), or

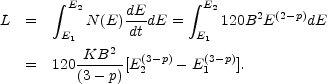(13.5)

For p = 2.5, and q₀ = + 1, L ~ 10⁴⁴ z²S, where S is the flux density at 1 GHz. ²

Eliminating K between Equations (13.4) and (13.5) we have

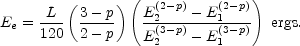(13.6)

Using Equation (1.8) to relate E₂ and E₁ to the cutoff frequency and grouping all the constant terms together,

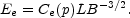(13.7)

The total luminosity L of the source may be estimated by integrating the observed spectrum between 10 MHz and 100 GHz. The magnetic energy is obtained from

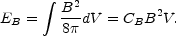(13.8)

The total energy in fields and particles (E_c = E_e + E_B) is minimized when dE / dB = 0 or when

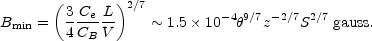(13.9)

The value of B estimated in this way must be treated with caution. It depends almost entirely on the angular size, , and is relatively insensitive to the flux density, distance, or spectral index.

From Equations (13.7), (13.8), and (13.9), if is expressed in arcseconds, then

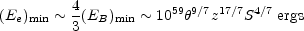(13.10)

and depends only weakly on p. Thus, the minimum energy is given when the energy is nearly equally distributed between relativistic particles and the magnetic field, and this is usually referred to as the minimum energy or equipartition case.

Typically, the total energy contained in the extended sources is estimated to be in the range of 10⁵⁷ to 10⁶¹ ergs and the magnetic field between 10^-6 and 10^-4 gauss. Under these near equilibrium conditions (E_e ~ E_B), the total energy depends to a large extent on the size of the source (E r^9/7). Thus the larger sources with low surface brightness and low luminosity, such as Centaurus A, are calculated to contain almost as much energy as the smaller but much more powerful high-surface-brightness objects such as Cygnus A or 3C295. However, high-resolution observations indicate that in many sources the observed radio emission comes from only a small fraction, , of the projected volume. The minimum total energy calculated from Equations (13.9) and (13.10) is then multiplied by a factor of ^3/7, and the corresponding magnetic field is increased by the factor ^-2/7. It is by no means clear that minimum energy, or equivalently equipartition, conditions hold in extragalactic radio sources. Moreover, the value of the fill-in-factor , is very uncertain, and calculation of energy content or magnetic field strength based on minimum energy or equipartition arguments must be treated with caution.

For some years it was widely thought that the relativistic electrons were secondary particles produced as the result of collisions between high-energy protons. If the ratio of the number of protons to electrons is k, then the minimum total energy is increased by a factor of (1 + k)^4/7 and the magnetic field by (1 + k)^2/7. Some estimates of the value of k were as high as 100, with a corresponding increase in energy requirements by about an order of magnitude. Elimination of the factor k and inclusion of the fill-in factor , can easily reduce the minimum-energy estimates by two or more orders of magnitude.

A more direct, although not necessarily more accurate, method of determining the magnetic field in extended extragalactic radio sources is based on the scattering of the microwave background radiation by the relativistic plasma. The ratio between the synchrotron radio flux and Compton scattered X-ray flux depends on the magnetic field strength and is given approximately by (Miley 1980)

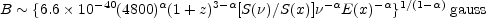(13.11)

where S() is the radio flux density at frequency and S(x) is the X-ray flux density at energy E(x). Values of B estimated from Equations (13.9) and (13.11) are in the range of 10^-6 to 10^-4 gauss, so that the energy content appears to be close to the minimum requirement. But estimates of B from Equation (13.11) are subject to error if the thermal X-ray flux is not negligible compared with the Compton scattered X-ray flux.

In a 10^-4-gauss field, electrons radiating at > 1 GHz are expected to decay in about 10⁶ years (Equation 1.8). Thus, the absence of any observed spectral cutoff even at >> 10 GHz suggests continued acceleration of relativistic particles. Even more restrictive limits are imposed by the observation of both radio and optical ( ~ 10¹⁴ Hz) synchrotron emission from the M87 jet at least 10 kpc away from the nucleus (Biretta et al. 1983a).

Because an adiabatically expanding cloud of relativistic particles loses energy as R^-2p (e.g. Kellermann and Pauliny-Toth 1968), it has been argued that if the observed relativistic electron clouds had expanded adiabatically from a much smaller region, the initial energy requirements would be prohibitively large. Although a variety of models have been discussed which allow some of the kinetic energy of expansion to be converted into relativistic particle energy, the adiabatic loss problem has been a prime motivation for models which consider the primary energy source to be in a compact region at the quasar or AGN with the energy being transported from this "central engine" to the outer lobes by a relativistic beam. (Section 13.4.1). However, it has also been pointed out by Bicknell (1986) and others that if the source has expanded to some final size and another burst of particles occurs, without significantly expanding the source, then no further adiabatic losses occur.

² Numerical expressions given in this chapter are evaluated for H = 100 km s^-1 Mpc^-1, q₀ = 1, and p = 2.5( = 0.75). More general formulations for other values of and more complex geometries are given in Moffet (1975), Jones et al. (1974a, b), and Marscher (1983). Back.