4.3. Polarization

The Chandrasekhar (1960) calculation of polarization emerging from pure electron-scattering atmospheres is unlikely to apply to real accretion disk atmospheres, which have nonzero absorption opacity. Laor, Netzer, & Piran (1990) made the first attempt at calculating the effects of absorption opacity on the disk polarization of AGNs. They did this by simply multiplying the Chandrasekhar polarization by the ratio of Thomson opacity to total opacity,

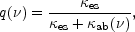(2)

which they took to be independent of depth at each radius in the disk. Because q < 1 at all frequencies by definition, this gives the physically reasonable result that absorption opacity always reduces polarization. The total disk polarization was therefore reduced in their calculations, which therefore produced better agreement with observations. Once again we note, however, that their models may have had high photospheric densities and therefore might have exaggerated the importance of absorption opacity compared to scattering opacity. In general they predicted that the polarization should rise with decreasing wavelength up to around the Lyman edge, then drop because of the increase in bound-free opacity, and then rise again. Laor et al. (1990) also included the effects of the relativistic transfer function on polarization and found that at very short wavelengths the plane of polarization rotates away from being parallel to the disk plane.

The effects of absorption opacity on polarization can actually be more subtle than assumed by Laor et al. (1990). Polarization emerging from an atmosphere depends on both the presence of scattering opacity and the degree of anisotropy of the radiation field (limb-darkening or limb-brightening). While absorption opacity reduces the importance of scattering, it can also enhance the anisotropy, depending on the thermal source function gradient. This can sometimes lead to an increase in polarization over and above that expected for a pure electron-scattering atmosphere (Harrington 1969; Loskutov & Sobolev 1979; Bochkarev, Karitskaya, & Sakhibullin 1985). The effect is illustrated in Figure 21, which shows polarization as a function of q for thermal source functions that vary linearly with total optical depth in the atmosphere:

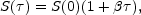(3)

where the constant determines the steepness of the thermal source function gradient. As shown in the figure, inclusion of absorption opacity (q dropping below unity) can produce an increase in polarization if the thermal source function gradient is steep. In addition, flat thermal source function gradients can produce strong negative polarizations, in which the polarization is perpendicular to the disk plane (the "Nagirner effect"). The Nagirner effect might be one way of reconciling the fact that the polarization observed in AGNs is parallel to the radio axes and perpendicular to the Chandrasekhar (1960) prediction. However, it may be difficult for it to produce an optical polarization which is wavelength independent, as observed.

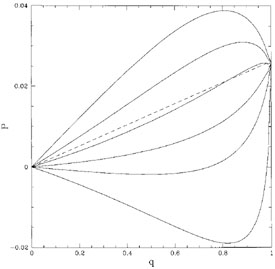Figure 21. Polarization as a function of the ratio of scattering opacity to total opacity q for various values of the thermal source function gradient . From bottom to top, the solid curves represent = 0, 0.5, 1, 2, 5, and . The dashed line is the approximation used by Laor et al. (1990). The observer inclination angle is 63° for all curves. All curves approach the Chandrasekhar (1960) value for this inclination angle as q 1, the pure electron-scattering limit. Positive values of polarization correspond to the plane of polarization being parallel to the disk plane, while negative values correspond to the plane of polarization being parallel to the disk symmetry axis. (figure modified from Agol et al. 1998a).

Blaes & Agol (1996) attempted to use these atmosphere effects to explain the steep rises in polarization observed blueward of the Lyman edges in some quasars, discussed above in Section 3.3. A good qualitative fit was obtained to the data for PG 1222+228 (Impey et al. 1995) by invoking a relatively cool disk whose overall SED turns over in the Lyman edge region (see Fig. 22). As discussed in Section 4.1, this may be a way of explaining the red SEDs observed in quasars. However, a quantitative fit was not achieved, and the predicted polarization rise is not as steep as observed. Moreover, they were unable to explain the very steep rise observed in PG 1630+377 (Koratkar et al. 1995). In addition, they neglected the relativistic transfer function, which tends to smear and reduce the polarization rise (Agol 1997; Shields, Wobus, & Husfeld 1998), although this may not be a problem if the optically thick portion of the disk does not extend all the way down to the innermost stable orbit.

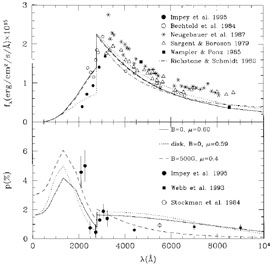Figure 22. Flux and polarization vs. observed wavelength (z = 2.047) of PG 1222+228. The solid curve is a fit for a single atmosphere with effective temperature of 20,000 K and surface gravity of 130 cm s-2. The dashed curve shows a fit with the same model but including Faraday rotation effects. Finally, a fit for a standard thin accretion disk model is shown as a short dashed line (from Blaes & Agol 1996).

Shields et al. (1998) have produced a model that produces excellent quantitative agreement with the observations of steep polarization rises near the Lyman edge but is based on ad hoc assumptions. They assume that at every radius the disk produces a spectrum with a sharp Lyman edge in absorption, together with a large Lyman polarization edge in emission. In particular, the polarization is assumed to be zero redward of the edge and an arbitrarily high multiple of the Chandrasekhar (1960) pure electron-scattering polarization blueward of the edge. These spectra are then passed through the relativistic transfer function and can be made to fit the observations quantitatively with few free parameters (see Fig. 23). This is a considerable achievement, but it relies on having a large intrinsic polarization jump at the Lyman limit from the disk. Shields et al. suggest that this might be produced by Lyman continuum photons emitted and scattered by an optically thin, ionized region of the accretion disk, but this remains to be demonstrated. The relativistic transfer function is crucial to their fits, and they require the disk to be viewed nearly edge-on (all their successful fits had inclination angles greater than 75°). The Blaes & Agol (1996) models also required rather large inclination angles (53° - 66°).

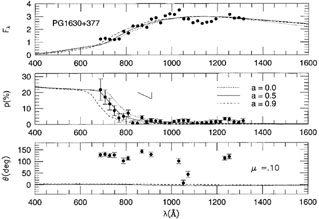Figure 23. Flux (top), degree of polarization (middle), and polarization position angle (bottom) model fits to the observed data of PG 1630+377, from Shields et al. (1998). The position angle of the accretion disk axis is unknown, so the overall offset in angle in the bottom figure is not significant. The inclination angle of the disk is assumed to be 84° (nearly edge-on). Different black hole spin parameters a in units of M are shown. The accretion disk models assume a polarization locally emitted by the disk of zero redward of the edge and 4.4, 4.4, and 5.7 times the Chandrasekhar (1960) value blueward of the edge for a / M = 0, 0.5, and 0.9 respectively (courtesy G. Shields).

One of the more successful theoretical solutions to the Lyman edge problem in total flux has been Comptonization of the intrinsic disk spectrum by a corona. Comptonization will of course imprint its own polarization signature on the emerging spectrum. Hsu & Blaes (1998) have presented radiative transfer calculations of Compton scattering of polarized radiation in two-phase accretion disk models with plane-parallel geometry. For featureless spectra, Compton scattering generally produces less polarization than Thomson scattering with the same optical depth. Nevertheless, when Compton scattering is sufficient to smear out a Lyman edge, it generally produces significant polarization in the overall spectrum. Interestingly, Compton scattering can produce very large polarizations parallel to the disk axis blueward of an input Lyman edge, and at the same time the edge is smeared out in total flux. However, the rise in polarization magnitude is not steep enough to explain the rises observed in several QSOs (see Section 3.3).

Lee & Blandford (1997) suggested that resonance line scattering by an externally illuminated slab may explain the high polarization seen shortward of the Lyman edge in PG 1630+377. To test this model further, we need high-resolution spectropolarimetry in the rest wavelength range 500-1000 Å.

It may in fact be that optical/UV radiation emerging from the accretion disks of AGNs exhibits very little polarization. Magnetic fields are widely believed to play an important role in accretion disks, and they can significantly reduce the polarization emerging from the disk photosphere through Faraday rotation (Gnedin & Silant'ev 1978; Blandford 1990; Matt, Fabian, & Ross 1993; Begelman 1994). The Faraday rotation angle at wavelength is 0.1_T( / 5000 °Å)²(B_|| / 1 G), where _T is the Thomson depth near the scattering photosphere and B_|| is the component of field strength along the line of sight. The equipartition field strength in the inner regions of an disk is ~ 10⁴ G ^-1/2 (M / 10⁸ M)^-1/2. Hence unless the filling factor of magnetized regions on the disk photosphere is very small, the optical (and UV perhaps) radiation from the disk should be completely depolarized. Detailed polarized radiative transfer calculations through disks with pure electron-scattering atmospheres confirm this (Agol & Blaes 1996). Complications arise when absorption opacity is included, but generally the effect of magnetic fields is still to reduce the overall polarization. The only exception is when the Nagirner effect is present, where modest magnetic fields can actually increase polarization (Agol, Blaes, & Ionescu-Zanetti 1998a).

If Faraday rotation or some other process wipes out optical continuum polarization from the accretion disk photosphere, then one must still find an explanation for the small polarization that is actually observed. One possibility is dust and electron scattering in a stratified wind on scales much larger than the central accretion flow. This mechanism is capable of explaining both the large perpendicular polarizations in Seyfert 2 galaxies and the small parallel polarizations in Seyfert 1 galaxies in a manner consistent with unification schemes (Kartje 1995). Thomson scattering in a fast wind near the accretion disk is also capable of producing polarizations parallel to the disk axis (Beloborodov 1998) because relativistic aberration makes the radiation field limb-brightened in the rest frame of the scattering electrons.

The current spectropolarimetric observations place strong constraints on the models. The low polarization observed in AGNs indicates that if electron-scattering-dominated disk atmospheres are considered, then magnetic field effects must be included in the calculations.