


The only result that seems to emerge with some clearness is
that the spiral arms are permanent features of the nebulae
[...] perpetuated in static form.
Jeans 1929, p.360
1.1. From unstable orbits to global wave modes
It is natural that in this field, on which at that time nothing
was ripe for harvesting, he did not immediately find the right
path.
Oort 1967, p.333
Though the fact of our larger-scale universe had begun to emerge through Hubble's work, it was not yet as clear on the quantitative side: well advanced in rank, the `nebulae' still came short of size and mass against our Galaxy. This was made by the underrated galaxy-distance scale, 5 and the giant ellipticals, missing in the Local Group and nearby, got it the most. On the whole, the ellipticals were found to be one to two orders under the spirals, and the rather enigmatic barred galaxies were ranged somewhere intermediate (Hubble 1936).
Original absorption-spectrum methods of detecting the galaxy rotation were sensitive only for bright central regions of comparatively close systems, the line inclination being established integrally, as a quantitative measure of overall uniform rotation. The emission-spectrum methods, in practice since the late 1930s, could as well catch the kinematics of the rather distant regions in our next-door spirals M31 and M33 (Babcock 1939, Mayall & Aller 1942). Limited and inaccurate though these data were (Fig.1), they took astronomers by storm and for almost two decades then they formed and served the idea of a standard rotation curve. The latter was understandably professed to obey V(r) = ar / (1 + b r2) and be scaled so as to co-measure its rising part to a live galaxy within its `visible boundary'. 6,7 And on the barred spirals it was disarmingly clear "with no measurement" at all that in face of rapid bar destruction their rotation was nothing, if not uniform (Ogorodnikov 1958, p.517).
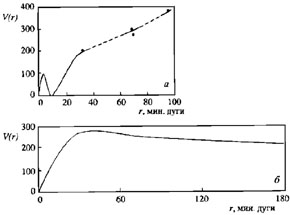 |
Figure 1. The rotation curve of the galaxy M31: a - as provided by the late-1930s optical data (Babcock 1939), b - as inferred from the mid-1950s radio data (Hulst et al 1957). |
Genuinely matched with the empirical climate were the theoretical tastes of the epoch that followed closely Jeans' directive on unified cosmogony of galaxies and stars. 8 One relied on the study of gaseous figures; they were diagnosed to be open to evolutive secular instability created by dissipation factors acting in the steady-motion systems. The latter just "never attain to a configuration in which ordinary [dynamical] instability comes into operation" (Jeans 1929, p.199), so that "it is secular stability alone which is of interest in cosmogony" (Jeans 1929, p.214) 9 . Quite understandably, Lindblad's early work lay nearby in the feeling for global evolutionary processes. 10 Yet he was the first, and for more than thirty years almost the only one, who singled out the spiral problem and treated it as a separate, stellar-dynamical element in the general philosophy of galaxies. 11
Lindblad started from a highly flattened lens of stars in uniform rotation
( = const,
A = 0 in Eqn (1)) created in the course of primary evolution
(Lindblad 1926a,
1927a).
Gravitational potential at its edge
changes so abruptly with radius that circular orbits there get unstable
(
= const,
A = 0 in Eqn (1)) created in the course of primary evolution
(Lindblad 1926a,
1927a).
Gravitational potential at its edge
changes so abruptly with radius that circular orbits there get unstable
( 2 < 0):
those inside of, but close to, the edge need only a
slight individual change in energy in order to be transformed into
quasi-asymptotic orbits extending very far from the `mother system' (the
solar neighborhood belongs exactly to some such exterior that shows
differential rotation obeying relations (1)). Still stars leave and return
to their mother system spontaneously and equiprobably in any point on its
edge, which is not conducive to neat global patterns. But the hitch is
removed upon the admission of either an outside disturber or an overall oval
distortion caused by fast rotation.
12 In both cases, two
opposite ejection points arise on the
edge of the lens after a transitory process and, fixed in space, they pour
material out in spiral-looking leading gushes. Turning to
intrinsic mechanisms of
galaxy structures, Lindblad laid greatest stress upon global modes of
disturbances, called the deformation waves (`uncompressible' modes) and the
density waves (`compressible' modes), and sought their unstable
solutions (Fig.2).
13 Analyzing
the effects such waves had on stars on asymptotic orbits
(Fig.3), he
proposed and refined scenarios of spiral-arm formation in an outer, shearing
galaxy envisaged to keep up somehow the patterns as arranged by a mass of
the affected orbits, rather than to destroy them
(Lindblad 1927a,
1948,
1953).
14,15
2 < 0):
those inside of, but close to, the edge need only a
slight individual change in energy in order to be transformed into
quasi-asymptotic orbits extending very far from the `mother system' (the
solar neighborhood belongs exactly to some such exterior that shows
differential rotation obeying relations (1)). Still stars leave and return
to their mother system spontaneously and equiprobably in any point on its
edge, which is not conducive to neat global patterns. But the hitch is
removed upon the admission of either an outside disturber or an overall oval
distortion caused by fast rotation.
12 In both cases, two
opposite ejection points arise on the
edge of the lens after a transitory process and, fixed in space, they pour
material out in spiral-looking leading gushes. Turning to
intrinsic mechanisms of
galaxy structures, Lindblad laid greatest stress upon global modes of
disturbances, called the deformation waves (`uncompressible' modes) and the
density waves (`compressible' modes), and sought their unstable
solutions (Fig.2).
13 Analyzing
the effects such waves had on stars on asymptotic orbits
(Fig.3), he
proposed and refined scenarios of spiral-arm formation in an outer, shearing
galaxy envisaged to keep up somehow the patterns as arranged by a mass of
the affected orbits, rather than to destroy them
(Lindblad 1927a,
1948,
1953).
14,15
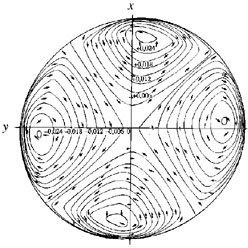 |
Figure 2. The m = 2 wave mode in Lindblad's bar-spiral density wave theory. Two wave maxima and minima are placed along the x and y axes, respectfully. These bisymmetrically located maxima and some extra concentration at a galaxy center are to explain the bar phenomenon. The arrows show systematic noncircular motions. (The figure is reproduced from Lindblad & Langebartel 1953) |
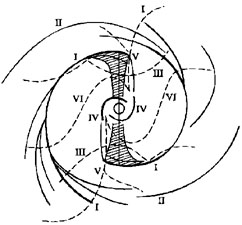 |
Figure 3. The formation of spiral structure as envisaged in Lindblad's bar-spiral density wave theory. (The figure is reproduced from Lindblad & Langebartel 1953) |
5 It was not until the early 1950s that the distance scale was reconsidered (see Baade 1963, Efremov 1989) and the size of the Local Group doubled. Given the shifted zero-point in the Cepheid-luminosity calibration, Hubble's constant was reduced, and by the 1960s it fell from its original 550 km/s/Mpc down to 180 (de Vaucouleurs) or to 80 (Sandage). This gave a 3-to-7-fold increase in distance. Back.
6 This form of V(r) emerged from the solution of Jeans' problem for an axisymmetric stationary stellar system with ellipsoidal velocity distribution. It greatly encouraged work on modeling the three-dimensional gravitational potential and mass distribution in the Galaxy (Parenago 1950, 1952; Kuzmin 1952; Safronov 1952; Idlis 1957). Back.
7 "Both in M31 and M33 the easily visible spiral arms lie in regions where the rotation does not deviate strongly from uniformity. It is remarkable in M31 that outside the nucleus [...] there is another region of nearly uniform rotation" (Weizsacker 1951, p.179). Vorontsov-Velyaminov (1972) was still confident that near uniform rotation was the type adopted by most of spiral galaxies. Back.
8 The idea of an overall one-time star formation early in the life of our Galaxy had long been predominant. In the late 1930s only the hydrogen-to-helium-synthesis energy source was proposed. That allowed evaluation of the fuel exhaustion time at a given star luminosity, and its shortness for the blue supergiants - 107 yrs - exhibited star formation as an ongoing process. This idea gained empirical support during the 1940s. Back.
9 In Jeans' view (Jeans 1929, p.213), as a nebula in uniform rotation shrinks, it alters (augments) density, not angular momentum, running through a one-parameter sequence of equilibrium figures. Remarkably, this same sequence is followed by a non-compressible liquid body as it enhances its momentum. According to Poincare, this body is secularly stable till it is a low-flattening Maclaurin spheroid. But when some critical eccentricity (momentum) is reached, it looses stability, takes another sequence of stable equilibrium figures - Jacobi ellipsoids - and then follows it at speedier rotations. Back.
10 "Now it is obvious
from the scheme as Hubble described it that he had an impression or a
belief, although he never quite admitted it, that it represented a
continuous sequence. But I believe, on the contrary, that Lindblad put his
finger on the essence of Hubble's classification when he suggested that it
is a series of increasing flattening, or increasing angular momentum"
(Baade 1963, p.16-17).
"According to Lindblad's theory, the fully
resolved spiral pattern is regarded as an advanced state which all nebulae
will eventually reach in the course of their evolution"
(Chandrasekhar 1942,
p.180).
Back.
11 The trend of this philosophy is sensed through the following reflection by Weizsacker (1951, p.165): "The evolution of a single object can be understood only if its temporal and spatial boundary conditions and the external forces acting on it are known. These are defined by the evolution of the larger system of which the object forms a part. So every single problem is likely to lead us back into the problem of the history of the universe". Back.
12 Circular orbits at the spheroidal edge are unstable for eccentricities e1> 0.834, and as the level e2 = 0.953 is achieved (3.1:1 axis ratio), dynamical instability against the two-crest harmonic sectorial waves is thrown in, so that the figure gets oval. Back.
13 "The most important modes of density
variation" appear to be of the type of ~ (r / R)m
cos( t -
m
t -
m )
(
)
( and m being wave frequency and azimuthal wavenumber, R -
the lens radius).
"The conditions for instability have been investigated for the waves
m = 1, 2,
3. The greatest interest attaches to the wave m = 2 because it
tends to explain
the formation of barred spirals. The density variation is accompanied by the
development of four whorl motions. [...] The disturbances due to the
four whorls on the motions in a surrounding ring structure [the latter
thought of as having been formed previously] explain in a qualitative way
the development of spiral structure"
(Lindblad 1962, p.147).
Back.
and m being wave frequency and azimuthal wavenumber, R -
the lens radius).
"The conditions for instability have been investigated for the waves
m = 1, 2,
3. The greatest interest attaches to the wave m = 2 because it
tends to explain
the formation of barred spirals. The density variation is accompanied by the
development of four whorl motions. [...] The disturbances due to the
four whorls on the motions in a surrounding ring structure [the latter
thought of as having been formed previously] explain in a qualitative way
the development of spiral structure"
(Lindblad 1962, p.147).
Back.
14 These articles provide a reasonable summary of Lindblad's theories prior to 1955. The asymptotic-spiral theory was thoroughly reviewed by Chandrasekhar (1942), and the wave-mode theory by Zonn & Rudnicki (1957). See also (Lindblad 1962; Contopoulos 1972; Toomre 1977, 1996; Pasha 2000). Back.
15 In Lindblad's bar-mode theory as it had progressed by the early 1950s (Lindblad & Langebartel 1953), three factors serve for the spiral formation. The first is the tendency for the formation of the rings, one at the galaxy center and one (or several) more in the distance, the bar occupying the inter-ring region. The second factor is the development of two diametrically opposed zones of enhanced density (see Fig.2). The third one is the increased centrifugal (radial) motion in these zones. If the bar-forming processes affect the galaxy kinematics but weakly, then the motions of distant material lag behind that of the main galactic body, and as the existing radial motions make the outer ring deform and break up, it forms the main spiral arms (I and II in Fig.3). Also, the effects of the bar wave show that material at the bar `tips' has some extra rotation, so that, helped by the radial motions, it forms the inner spiral arms (VI in Fig.3). If the galactic angular momentum is above some certain level, the density wave can give no bar, and the deviations from axial symmetry it causes produce the appearance of ordinary spiral structure. Back.