1.3. Winds of change

The spiral structure is nothing more than a tracer element
contained in a fairly uniform disk of material [...] This is
probably related to the magnetic field in the disk.
G. R. Burbidge 1962, p.295

As far as I am aware, no single problem, not even a stability
problem, has been solved in a differentially rotating self-gravitating
medium. Even without magnetic fields, and even
linearizing the equations, it is very hard to make progress.
Prendergast 1962, p.318

With our observations we have reached a point where we
are simply unable to draw any definite conclusion, unless the
theory helps us. I hope some day there will be action, because
otherwise we are lost.
Baade 1963, p.266

The post-war success in galaxy research gave priority to the empirical approach. By the late 1950s, it formed two flanks of evolutionary studies, morphological and quantitative. The first one, due mostly to the Palomar sky survey, called for elaborate classifications, catalogs and atlases of galaxies (Zwicky 1957; Morgan & Mayall 1957, de Vaucouleurs 1959; Vorontsov-Velyaminov 1959; Sandage 1961); the second exploited matters concerning stellar evolution and empirical data on individual galactic objects. As regards the theoretical approach, it too branched under the new conditions and its subject was now treated in distinct frames of physical, chemical and dynamical evolution.

On this dynamical side, the one to our present interest, true lodestars started shining by the 1960s. One of them was lit by the linear stability theory as applied to long-range force systems; denied so far, mostly by human inertia, its methods eventually penetrated into the galaxy dynamics. ²⁶ Chandrasekhar (1953, p. 667) formulated the problem as follows:

"When we know that an object has existed in nearly the same state for a long time we generally infer that it is stable; and by this we mean that there is something in its construction and in its constitution which enables it to withstand small perturbations to which any system in Nature must be subject. [...] Thus when we are confronted with a novel object - and most astronomical objects are novel - a study of its stability may provide a basis for a first comprehension".

To him, however, it was a matter of pure intellectual interest, above all. "For an applied mathematician, Chandrasekhar explained, problems of stability present a particular attraction: by their very nature, these problems lead to linear equations and linear equations are always more pleasant to deal with than nonlinear ones" (Chandrasekhar 1953, p.667). ²⁷ In so thinking, he turned to most general, technically transparent models. One of such was Jeans' infinite homogeneous medium asked about whether the classical stability criterion k² c² - 4 G > 0 and the critical fragmentation scale _J = ( c² / G )^1/2 remain unchanged if the medium is involved in uniform rotation (ñ and are sound speed and material volume density; k, and = 2 / k - wave number, frequency and length; G -gravity constant). ²⁸ The answer came positive, with the one exception for perturbations propagating in the direction just at right angles to the rotation axis, when Coriolis force co-governs wave dynamics and modifies the dispersion relation into

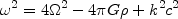(2)

showing that any rotation with > ( G )^1/2 entirely prevents the system from decay.

Safronov (1960a, b), interested in protoplanetary cloud dynamics as a part of his solar-system cosmogony, examined a more realistic model - a differentially rotating gas layer stratified along the rotation axis. ²⁹ A short-wave analysis led him to a relation

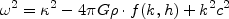(3)

that basically differed from Eqn (2) in its modified gravity term depending on both wavenumber and the layer's thickness h. The correction factorf (k,h) evaluated, Safronov found - quite in Jeans' spirit - that rotating flat systems lose stability and must break up into rings as soon as their equilibrium volume density gets above some critical value.

In that same 1960, first results were supplied by collisionless collective dynamics, concerning the simplest, spherical systems. ³⁰ Antonov (1960) found for them the now classical "stability criterion, rather complicated though", and Lynden-Bell (1960a) discovered a peculiar feature of their equilibrium states - the ability of collisionless spheres to rotate. ³¹

Another lodestar for dynamical studies was the evidence provided by a bulk of higher-precision rotation curves obtained for spiral galaxies in the late 1950s by Burbidges and Prendergast. At long last, their general rotation was ascertained to be strongly differential. This fact, stripped now of all surmise, seriously warned astronomers that they were in the presence of a real problem of the persistence of spiral structure.

"There appears to have been some feeling in recent years that individual spiral arms are long-lived features in a galaxy. [...] However [...] we shall show that the form of the rotation-curves for spirals will insure that the spiral form will be completely distorted in a time short compared with the age of a galaxy" (Prendergast & Burbidge 1960, p.244).

The quantitative estimates did show that the data on M31, M81, NGC 5055 "and probably all similar spiral galaxies" were in conflict with "certain apparently reasonable assumptions" - namely, at least with one out of the following three: (a) only circular velocities are present in galaxy disks, (b) these velocities are independent in time, (c) material which is originally in a spiral arm remains in that arm (Prendergast & Burbidge 1960, p.244, 246).

The `urgent problem' of the persistence of spiral forms was taken up by Oort. Speaking at a 1961 conference at Princeton of "every structural irregularity" in a galaxy as being "likely to be drawn out into a part of a spiral", he called for another phenomenon to turn to and conceive:

"We must consider a spiral structure extending over a whole galaxy, from the nucleus to its outermost part, and consisting of two arms starting from diametrically opposite points. Although this structure is often hopelessly irregular and broken up, the general form of the large-scale phenomenon can be recognized in many nebulae" (Oort 1962, p.234).

Oort suggested "three ways out of this difficulty", one of which was that "the arms could retain their present spiral shapes if matter were constantly being added to their inner edges, while the outer edges would constantly lose matter" (Oort 1962, p.237-8). This possibility was given an eager discussion at the conference (Oort 1962, p.243).

Yet one more lodestar for galaxy dynamics was lit in the 1950s by numerical computer methods. They first served the calculating of three-dimensional star orbits; Contopoulos (1958, 1972) then stated their non-ergodicity and posed anew the problem of a third integral of motion. P.O. Lindblad, as we saw, turned the same Stockholm computer to studying the galaxy dynamics in terms of an N -body problem (Lindblad & Lindblad 1958; P.O. Lindblad 1962).

²⁶ "I cannot agree that plasma physics methods penetrated in astronomy in the 50's. Of course these developments helped each other, mainly in the 60's, but this is natural. I think that in the 50's progress was sporadic, due to the insight of only a few people, but later many people followed the first pioneers". (Contopoulos) Back.

²⁷ Particularly, this was the line in which the unified theory of ellipsoidal equilibrium figures was being developed later (Chandrasekhar 1969). "There was criticism by astronomers of Chandrasekhar's work on the classical ellipsoids because of its remoteness from the current needs of astronomy. Chandra's interest (and my own as well) was indeed motivated by non-astronomical considerations. What we found was a development by some of the great mathematicians of the 19th and early 20th century that had largely been forgotten, and in some mathematical respects was left incomplete. Chandra felt strongly that his work should, on general intellectual grounds, be completed. If that completion should have application in astronomy, so much the better, but that was not the motivation. His critics in astronomy were offended because he was not doing astronomy. Chandra, however, was more devoted to science (or his view of it) than to astronomy, and did not feel obligated to work on problems which were chosen for him by astronomers". (Lebovitz) Back.

²⁸ "I do remember that at the time I wrote the paper, the spiral structure of the galaxies was not even remotely in my mind. Besides my paper was concerned with the Jeans instability of a gaseous medium and not to a system of stars...However, I am quite willing to believe that the basic ideas were included in earlier papers by Lindblad". (Chandrasekhar) Back.

²⁹ Ledoux (1951), interested in the formation of planets from a primordial cloud, seems to have been the first to consider the stability of flat gravitating systems. He, as well as Kuiper who had turned him to this problem, suspected a change in the critical Jeans scale, realizing that an assumed cloud mass of about 10% that of the Sun would be enough for the cloud to act significantly on itself in the plane of symmetry. Ledoux found that for small adiabatic disturbances to the equilibrium state of an isothermal non-rotating layer Jeans' criterion remains unaltered if is taken to be half the density value at z = 0. This did give only a correction to the clumping scale, which was of order 2 times the thickness. Fricke (1954) combined the efforts by Ledoux (1951) and Chandrasekhar (1953), yet he too could not escape certain arbitrary assumptions. And Bel & Schatzman (1958), having returned to Chandrasekhar's model, let it rotate differentially - in violation of the equilibrium conditions, though. Back.

³⁰ Vlasov, a renowned plasma physicist, contributed to galaxy dynamics as well, via his article (Vlasov 1959) that had a special section "Spiral structure as a problem of the mathematical theory of branching of solutions of nonlinear problems". Through the collisionless Boltzmann and Poisson equations, he examined the equilibrium of an immovable plane-parallel slab, re-derived its density profile (z) ~ sech²(z / h), and `disturbed' eigenvalues of the equilibrium solution, wishing to establish the character of "infinitely close figures of equilibrium". His new solutions turned out "ribbed", or spatially periodic, with the "exfoliation period" being close to 3 kpc and corresponding to the scale of "stellar condensations observed by Oort". Despite some technical flaws (e.g., his basically smooth function (z) played as stepped one in integrations), Vlasov's conclusion about possible "ribbed" static equilibria in the tested slab was formally correct. Still, surprisingly (at least in retrospect), he gave no stability discussion, already practicable in contemporary plasma physics and very fitting as it would be for his galactic model. Back.

³¹ "This is in contradiction to Jeans' result, but is obtained by using his method correctly and following the consequences" (Lynden-Bell 1960a, p.204). Back.