2.3. Gravitational stability of flat systems

Lin asked [Woltjer in 1961]: What are the circumstances that
would be needed for either one or both of the stellar and inter-
stellar parts of a supposedly smooth galactic disk to remain
gravitationally stable against all large scale disturbances?
Toomre 1964, p.1217

The importance of collective effects in our Galaxy was first
clearly pointed out by Toomre (1964). He showed that in the
disk the stellar motions are sufficiently coherent to make it
almost vulnerable to collapse. He also pointed out that the
scale on which this would occur is quite large.
Kalnajs 1971, p.275

As we have seen, Safronov already raised the question of gravitational instability in flat rotating systems, aiming at the breakup of a protoplanetary cloud into detached rings. Toomre, interested in basically smoother objects like galaxies, turned in 1961 to a rather close, although opposite in accent, topic, and by the summer of 1963 he prepared an article "On the gravitational stability of a disk of stars" (Toomre 1964, hereinafter T64).

The paper started with the general presentation of the problem as it was then seen.

"The well-known instabilities of those Maclaurin spheroids whose rotational flattening exceeds a certain fairly moderate value suggest that the other sufficiently flattened, rotating, and self-gravitating systems might in some sense likewise be unstable. At any rate, these instabilities have been often cited as a likely reason why one does not observe elliptical galaxies exceeding a certain degree of oblateness. It is only when we turn to consider what are now thought to be the distributions of all but the youngest stars in the disks of the ordinary (as opposed to the barred) spiral galaxies that this classical result suggests a serious dilemma: How is it conceivable, in spite of these or analogous instabilities, that so much of the fainter stellar matter within such galaxies - and certainly the S0 galaxies - should today appear distributed relatively evenly over disks with something like a ten-to-one flattening?" (T64, p.1217)

The detailed study of the problem was preceded by a primary, qualitative stability estimate.

A rotating thin cold disk, in an approximate equilibrium between gravity and centrifugal forces acting on each mass element, is prevented from general contraction, still not from fragmentation. Small-size clumpings arise everywhere in such a disk, and then collapse, their gravity taking excess over rotation. But if larger-sized, they do not go as these two factors counteract each other. The demarcation length scale L_T proves plain co-measurable with the disk radius R. Thus the cold model, for all specifications it may have, is clearly unstable. ⁴⁷ The part played by random motions is best visualized with an immovable sheet model. There instability is avoided if stars (other mass elements), having an rms velocity ñ, cross a clumping zone in a time not exceeding that needed for an e -fold amplitude growth as registered in the cold case. Hence the largest yet ungrowing disturbance is found on an L_J c² / Gµ₀ scale, which is essentially the Jeans stability criterion. Now, letting the sheet rotate, one sees the two characteristic scales, L_T and L_J, be present (Fig.5). L_J gets closer to L_T for higher velocity dispersions, until they coincide at c's as high - in the order of magnitude - as the rotational velocity, thus meaning full stabilization against this sort of disturbances.

Figure 5. Characteristic scales in a gravitating disk. A cold rotating disk is stable for radial disturbances on the scales L > LT, a non-rotating hot disk is stable of scales L < LJ, a hot rotating disk is stable on both scales. As the velocity dispersion becomes of the order of the circular velocity, one obtains full axisymmetric stability.

The strict analysis of axisymmetric disturbances to a razor-thin disk, performed in T64, supported these rough estimates. In the cold case, it led to a local dispersion relation

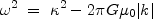(5a)

or

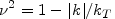(5b)

linking the wave frequency in units of , = / , with a critical wavenumber

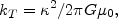(6)

the one to determine the shortest wavelength _T 2 / k_T of ungrowing (² 0) disturbances (Fig.6). ⁴⁸ The hot-disk analysis detected the minimum radial velocity dispersion at which the system is still resistant against all axisymmetric disturbances (Fig.7): ^49,50

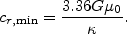(7)

The real-to-minimum velocity-dispersion ratio

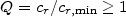(8)

thus got a local disk-stability parameter. ^51,52 In a marginally stable state Q = 1, disturbances of ₀ 0.55 _T proved most unpliant and barely suppressible. Our solar neighborhood would have such a ₀ 5 - 8 kpc, but if some Q 1 - 1.5 were not preferred empirically, implying a certain stability reserve. Of course, "it was as yet impossible to rule out instabilities altogether", but should any actually be present, they would not do with scales responding to the challenging 2-kpc spacings, as these "must almost certainly be judged as stable". This "is important as an argument against any suggestion that the existing spiral structure in this Galaxy might be the result of collective stellar instabilities" of the sort considered (T64, p.1236).

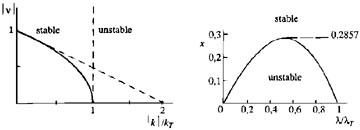Figure 6. (left) The dispersion relation curve for radial oscillations and tightly wrapped spiral waves in a cold disk. Figure 7. (right) The hot disk neutral stability curve. The disk is stable for all those the radial disturbances for which the parameter x = k2 cr2 / 2 exceeds xcr = 0.2857. This critical value determines the minimum velocity dispersion (7) sufficient to secure the axisymmetric disk stability. (The figure is reproduced from Toomre 1964)

"It follows that an initially unstable disk of stars should probably have undergone not just one but several successive generations of instabilities, after each of which the system would have been left somewhat less unstable than it was previously. In particular, it seems likely that before very many rotation periods had elapsed, the disk would have approached a new equilibrium state that was again fairly regular and quite possibly axisymmetric, but in which the random velocities at the various radii had become - and would henceforth remain - about equal to the minimum values needed for complete stability: (T64, p.1237)." ⁵³

Besides, since the total gravitational energy of the disk would have had to be the same during its evolution (the virial theorem), "the said redistribution of stars could not simply have consisted of an overall contraction, but would have had to entail a contraction perhaps in the inner parts of the disk jointly with a net expansion of the outer portions" (T64, p.1237) - as it was already seen by Lynden-Bell (1960b) from the gas-dynamical viewpoint.

As regards non-axisymmetric disturbances, it was pointed out in T64 that because of the specific action of the Coriolis force those are restrained even more effectively than radial disturbances, thus requiring no addition for c_{r, min}. However, Toomre remarked, a question that his discussion left "completely unanswered" was "to what extent a similar amount of random motion [Q = 1] might affect the character of the most extensive non-axisymmetric disturbances, in particular those which ought to determine whether or not a given disk might prefer to develop into a barlike structure" (T64, p.1235). ⁵⁴

⁴⁷ Toomre got this estimate by the fall of 1961 and was struck with the fact that nothing had ever been said on the thing just shocking with its as simply derivable inference that cold disks be prone to violent instabilities. (Toomre) Back.

⁴⁸ Analyzing axisymmetric disturbances to a flattened rotating cloud, Safronov (1960a, b) did not solve the Poisson equation. He was guided by the notice that short radial waves find adequate the cylindric approximation for a torus (ring). But the cylinder is the sum of `rods', or elementary cylinders whose individual gravity is given by a simple formula, so that the business is just to integrate in infinite limits the elementary contributions over longitudal and transversal variables xand z. There Safronov was not perfect, however. His gently stratified cloud turned a stiff 2h -thick plate as he took his introduced density function <sub>0</sub>(z) out of integration over z. His subsequent integration over xwas in an interval of ± /4; that, he argued, ensured a predominant contribution to the perturbed force (which is qualitatively true). Had he integrated in infinite limits, and first - most trivially - over x, the gravity term in his Eqn (3) would have become -2 Gk <sub>0</sub>(z / h)e<sup>-k|z|</sup> dz, and with the exponential factor serving as a thickness correction he would have accurately managed with any density profile - and, most obviously, would have found that in the zero-thickness limit that factor simplifies to unity, the integral just gives the surface density µ<sub>0</sub>, so that the gravity term converts into - 2 G µ<sub>0</sub> k, the form in which it was presented soon by Toomre (1964) in frames of `regular' methods of the potential theory. Back.

⁴⁹ To solve the Vlasov kinetic equation, Toomre used the characteristics method that for some three-dimensional purposes had already served Lynden-Bell (1962), who in his turn cited the original source (Bernstein 1958) where that method had genuinely helped with the general disperion relation for the mathematically similar problem with a Maxwellian plasma in a magnetic field. Back.

⁵⁰ Because of a technical error in Toomre's analysis, this minimum value was initially overestimated by 20%. Not so little if one considers that the difference in c_{r, min} for star and gas disk models (the latter case admits a much simpler analysis) reaches 7% only. It is this "substantial error" which was detected in 1963 by Kalnajs (cf. Sect. 2.4), as reported frankly in T64 (p.1233). Back.

⁵¹ Formally, the `Q -parameter' (8) was introduced by Julian and Toomre (1966). Back.

⁵² This quantitative analysis refines the above view of disk stabilization as it shows via Eqs (6) and (7) that locally the result is attained already once L_J / L_T = (3.36/2 )² 0.286 (0.25 in a gas disk). Back.

⁵³ Asked to reminisce on how he had originally understood those dispersion velocities "about equal" to the needed minimum in the new equilibrium state - on whether or not this was a factual suggestion of marginal stability of our stellar disk, or some extra amount was yet permitted for its stability - Toomre has responded: "It is hard for me to reconstruct from this vantage point what exactly I meant or hoped by that statement. Probably I was mostly just trying to rationalize the surprising fact which I had then unearthed that the minimum theoretically needed c_{r, min} and the observed amounts seemed to agree so well within their considerable uncertainties, meaning within a factor of 1.5 or thereabouts, rather than some 2 or 3 or 4 [...] From about 1966 onwards, I was surely of the opinion that any Q less than about 1.5 here was highly suspect, if not downright ludicrous, because of fierce heating of cooler disks by their embedded gas complexes. But that came a little later. In 1964 my views were no doubt more permissive toward Q = 1.0". (Toomre) Back.

⁵⁴ Real progress in the study of this problem first came half a decade later. Back.