3.2. A definitive (?) new prediction

A desirable feature of the WKBJ waves is their mathematical
simplicity; their physical relevance to the `grand design' of a
spiral galaxy is less transparent.
Kalnajs 1971, p.275

"Just how much did Kalnajs' study of axisymmetric oscillations influence our work? The simple answer is: very little, if at all" (Lin). Such is Lin's judgment regarding the results he had set out in the summer of 1965. ⁷⁷ Those got out of the printer in no less than one year (Lin 1966, 1967a), but an abridged and slightly updated version appeared as soon as February 1966, having become an "Outline of a theory of density waves" by Lin and Shu (1966), labeled `Paper II'.

The three issues reported a WKBJ-styled dispersion relation for the razor-thin hot disk,

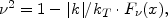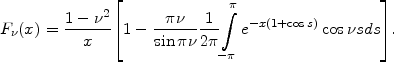	(17)

From its Kalnajs' axisymmetric analog (9)-(10) it differed in the Doppler shift included in and in the form of the reduction factor F(x). ⁷⁸ It was an idea of some such dispersion relation, Lin and Shu (1966) remarked, that had fed originally (LS64) their insight in the disk-stabilizing role of random motions. ⁷⁹

But an important dynamical, not chronological, point was that the hot rotating disk was seen to conduct radial and spiral waves rather distinctly. Given a state of marginal stability, the oscillatory radial neutral mode = / = 0 is well maintained by it along its medium radii (dying out at large r's), ⁸⁰ the local wavelength function ₀(r) depending on mass and angular momentum distributions. In contrast, the spiral wave cannot be neutral as extendibly: its Doppler-shifted frequency - m(r) gets r -dependent. This ties the neutrality condition = ( - m) / = 0 to a narrow corotation zone of r r_c, and there only can the interarm spacing (r) equal ₀(r), the rest of disk getting more and more stable against the wave as one travels away from r_c in or out. If so, why not to try to juxtapose the basic Lin-Shu concept of a balance and the solar-region stability inference by Toomre? For this, it seems sufficient to send corotation way beyond - to an outer disk region supposedly as permissive to marginal stability as to admit it - and to cancel all instability inside that r_c in favor of Q 1. Lin and Shu did seem to have followed this way. Moreover, they adopted a Q 1 model (discussed already in T64), being captured by a picture of overstability, i.e. gradient instability held to mildly develop over the system and to provide some selective amplification of trailing, not leading, waves.

Besides, relation (17) tells (k) to decrease with wavenumber till k remains under some k₀, and then to rise up at k back to unity. Any intermediate value of is met thus twice, meaning two branches of WKBJ solutions, the shorter- and the longer-wave ones, their forms r() being provided by equation (16) with F(x) added in the integrand denominator. If Q 1, the branches join at corotation, showing there equal interarm spacings _sw(r_c) = _lw(r_c) = ₀(r_c). This value is the largest (smallest) for the shortwave (longwave) branch: _sw(r) falls down until zero (_lw(r) ) as one goes from corotation to ILR. Aimed from the outset at explaining the observed 2-3 kpc local spacings, Lin got tempted to acknowledge the shortwave branch, the more so as, not to forget, in 1964 he had had no choice when having to comment on this same gas-given spacing on the basis of relation (14) that seized but one - long-wave (!) - branch. ⁸¹ But things did not get all as clear by 1966, and this is why neither Lin (1966, 1967a) nor Lin and Shu (1966) were eager to go into the wave-branch question, keeping silent about any graphic view of their newer formula. Only at the Noordwijk IAU Symposium (August, 1966) they gave a graph, it displayed the short-wave-branch extension of the () curve (Fig.10) on which they built a model for the full spiral of our Galaxy (Fig.11), tentatively two-armed and answered by a remote corotation (Lin & Shu (1967). ⁸² Spirals of this class show as slow a rotation as to almost guarantee the ILRs be present and lie in a relative proximity from the center. Namely, Lin and Shu connected our `home' m= 2 ILR with the `3-kpc arm' which fixed the spiral pattern speed _p = 11 km/s/kpc.

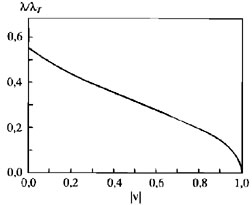Figure 10. The short-wave branch of the dispersion relation (17) for a Q = 1 disk model. (The figure is reproduced from Lin & Shu 1967)

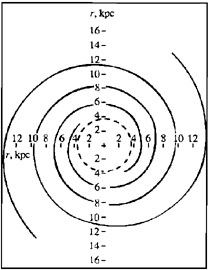Figure 11. The Lin-Shu model for the Galactic spiral density wave. The model is calculated with the help of the dispersion curve in Fig.10. The dashed line shows the ILR region taken to be the residence of the `3-kpc arm'. This provides the pattern speed p = 11 km/s/kpc. (The figure is reproduced from Lin & Shu 1967)

"My earliest recollection of realizing that there were separate long and short branches came when I was doing the numerical calculations for the spiral pattern that Lin wished to show at the Noordwijk symposium. As I recall, he was in the Netherlands and I remained behind at Harvard, and we corresponded by mail. I was considerably confused by which of the two branches should be used to generate spiral patterns (I had realized that a `reduction factor' applied to our 1964 formula was an incomplete description, and that long and short waves were implicit to Toomre's evaluation of a critical Q for axisymmetric disturbances). Finally, Lin suggested that we should simply choose the short branch by fiat as the practical thing to do given the press of the Noordwijk presentation, and we were left to try to sort things out later. That's my memory of the events". ⁸³ (Shu)

The Noordwijk diagram has been the first presentation of our Milky Way's density wave.

⁷⁷ Lin presented his first hot-disk results in June 1965 at a summer school at the Cornell University and at a mathematical symposium at the Courant Institute. These materials were published in two extensive articles (Lin 1966, 1967a) submitted in July. "I recall becoming aware of the relationship with the work of Kalnajs only when he brought up the issue in connection with Frank Shu's thesis presentation. I immediately recognized that there would probably be a way to make the connection through the application of the Mittag-Leffler theorem. Note that it is easy to derive the Kalnajs form from our integral form, but difficult to reverse the process. And our numerical calculations depended on the simple integral, since it was a time when large scale use of the computer was not yet available in a mathematics department. (I still remember the painful experience when my request - as chairman of the committee on applied mathematics - for a computer was turned down, even though the department had the funds. [...] Kalnajs might have been able to check the calculations with his infinite series through the use of the computer.)" (Lin) Back.

⁷⁸ "I have little knowledge but I make this conjecture: Kalnajs was studying axisymmetric oscillations, not standing waves of the spiral form, and obtained his results through the use of results for analogous oscillations in plasma waves. (I learned a lot about plasma physics only after Y.Y. Lau joined our research group.)" (Lin) Back.

⁷⁹ Lin agreed that the dispersion relation was already derived by Kalnajs "in the special case of axially symmetrical disturbances", but "by a quite different method" and "independently of the work of the author" (Lin 1966, p.902). He certainly appeared rather sensitive on the point of independence, beginning his spiral studies. His first appraisal of Lindblad's long-term emphasis on steady spirals was: "Indeed, independently of each other, B. Lindblad (1963) and the present writer came to the same suggestion of a quasi-stationary spiral structure of the stars in a disk galaxy" (Lin 1966, p.898). Again, referring time and again to different methods adopted by him and his various competitors, Lin found it difficult to closely compare those related issues. But, for example, Lynden-Bell (1962) and Toomre (1964) had used the same characteristics method as that taken in 1965 by Lin, with which he basically re-derived, again independently, this time from Toomre, that crucial differential equation of `asymptotic' disk-stability and density-wave theories (cf. Eqn (53) from T64 with Eqn (7.15) in Lin 1966 and Eqn (A20) in Lin et al 1969), not having mentioned its factual use by his next-door institute colleague. Back.

⁸⁰ Such behavior is well seen on Fig.3 from T64 showing results of numerical calculations of global radial modes for some illustrative cold-disk model. Back.

⁸¹ LS64 had assumed that because not all the stars but only those with smallest random velocities perceptibly contribute to the response of a disk, its effective surface density must be several times less than its full value. Back.

⁸² "This was my first meeting with the distinguished astronomers who made all the important observations related to spiral structure, many of whom worked under Oort's direction. Here we presented our first prediction of the spiral structure of the Milky Way, which remained to be an approximate representation, as indicated by Yuan's continual refinement over the years". (Lin) Back.

⁸³ "Lin and Shu 1966 emphasis upon (and the dispersion relation for) the short-wave branch of nearly axisymmetric WKBJ-style density waves, which is something that Kalnajs (1965) also knew from his thesis but failed to emphasize nearly as adequately, escaped me altogether even though the same for the long-wave branch as well as the stability criterion were plain as day from T64 - and to a more limited extent even from Safronov (1960a, b), as I often agreed in retrospect. I think my trouble was that my own ongoing work then with Julian (Julian & Toomre 1966) [...] had also sensitized me to the severity of phase mixing. [...] Looking back, this made me suspect until well into 1965 that all short stellar-dynamical waves, unlike their over-idealized gas equivalents, would in fact be strongly damped and were probably not of much value. And right there I have cheerfully agreed for about 34 years now that Lin and Shu (and as an independent authority also Kalnajs, not at all to be omitted) together proved me to have been spectacularly wrong". (Toomre) Back.