1.2. Swing amplification

In the severe amplification, Goldreich and Lynden-Bell offered
one real nugget of a discovery. ⁷
Toomre 1977, p.474

Lynden-Bell (1960) had already tried to materialize his spiral-regeneration idea. He was then riveted to strict modal analyses of gas sheets which applied in the case of rigid rotation only, but he hoped their sensible modifications would nevertheless give him a correct view of the effects of shear. He found this way misleading, yet he retained his original interest. ⁸ Goldreich told Lynden-Bell when they met that Gold, his thesis advisor, had imagined some such concept, too, but could not work it out. ⁹ He also told that with Gold's influence his own reflections on the spiral-winding problem and the fact that young stars are concentrated in the arms had set him to thinking about local gravitational instability in differentially rotating disks. Lynden-Bell immediately appreciated this small-scale approach, and they took it up together.

Imagine a washboard-like sinusoidal disturbance with its parallel crests and troughs oriented initially at some arbitrary, perhaps even `leading', angle with respect to the galactocentric direction. The basic differential rotation of that region of a galactic disk will slide (shear, swing) that density pattern as if it were painted material, except that the sinusoidal disturbance is itself a wave and its own amplitude will evolve amidst the shearing. To explore the actual character of this time evolution, GLB figured out a neat 2^nd-order differential equation (almost as if for a mass vibrating on a string, though now with a time-variable spring rate). In that way that they discovered that such special waves can get amplified very strongly indeed as the shear sweeps them around through the fully open orientation, especially in the case when their gaseous equivalent (Goldreich & Lynden-Bell 1965a) to Toomre's Q is as low as unity and the azimuthal wavelength _y matches Toomre's (1964a) axisymmetric critical _T (Fig.1).

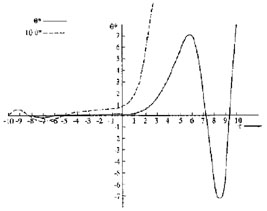Figure 1. Amplitude amplification of a wave in the course of its swinging from leading ( < 0) to trailing ( > 0). (The figure is reproduced from Goldreich & Lynden-Bell 1965)

Specifically, GLB considered a patch of a gravitating gas sheet, small and distant from the rotation axis to allow rectangular geometry and neglect radial variability of all its characteristics except angular speed (r) defining the shear rate A = - 1/2 r d / dr. They attached co-moving axes x and y, oriented one radially and the other along the flow, to shearing material and explored in new axes x' = x, y' = y + 2Axt wave harmonics of the form exp[i(k_x x' + k_y y')] = exp[ik_y(y - x)]. Each of them knew its invariable azimuthal wavenumber k_y and turned by the shear `clock hand' = 2At - k<sub>x</sub> / k<sub>y</sub> (pointing radially at = 0) in the amplitude control of an inhomogeneous in differential equation. <sup>10</sup> In its structure, shown by GLB to be the same for infinite and finite thickness models, <sup>11</sup> they read the behavioral scheme of such waves. At initial stages of their leading orientations the inter-crest spacing is small and gas pressure ensures stability. As the waves are swept round, rises (right up to <sub>y</sub>), the pressure loses its effect, and the net shear comes into play. It tends to feed genuinely `well-organized' gas perturbations, and the waves get amplified. ¹² But by the time of their considerable trailing there comes the renewed dominance of the pressure term and, with it, renewed oscillation, now at a largely enhanced amplitude. ¹³

⁷ The now accepted term swing amplification had been introduced not in the original GLB and JT papers of the mid-1960s, but some 15 years later, in one of Toomre's conference talks (Toomre 1981). Back.

⁸ "I was already at work on the spiral problem in 1959-60, and an outline of the changing wavelength stabilizing modes as they get sheared is given in my thesis with the deduction that probably this theory of spiral structure will not work. One chapter was nevertheless entitled "Towards a regenerative theory of spiral arms."" (Lynden-Bell 1964d) Back.

⁹ "I imagine we are but the present end of a long line of people who believed these ideas", Lynden-Bell reacted (1964d). Back.

¹⁰ "I remember Peter coming into my room saying he had an interest in spiral structure and that he did not know how to solve the problem but had figured out what coordinates to use. He then told me about his shearing coordinates which were the key to that work." (Lynden-Bell)

"I certainly didn't solve anything substantial, but I believe that I recognized that these coordinates exchanged homogeneity in time for that in x. This was probably the most important contribution I brought to my collaboration with Donald. [...] I don't know whether shearing coordinates had been used in fluid problems before GLB. However, they are such a normal choice that it would surprise me if that had not been." (Goldreich)

The sheared disturbances were adopted in the first papers on the non-axisymmetric local dynamics of galactic disks (GLB; Julian & Toomre 1966). More classical, separable forms A(r) exp[i t - m )] were recognized in the spiral-mode context just one or two years earlier (Lin & Shu 1964; Hunter 1963; Kalnajs 1963). (Lindblad had long ago been using them in his cumbersome bar-spiral theories. Contopoulos recalls (Contopoulos) that when in 1962 he told Lin about Lindblad's work in some detail, Lin took with him to MIT a batch of the latter's articles but then confessed that he did not understand them and preferred to start working from the scratch.) The interconnection of these two types of disturbances was for years questionable, and, for instance, Hunter who commented on it in his 1972 review criticized the "seemingly arbitrary decision" about using shearing axes and their related Fourier-analysis, pointing out that although it leads to solutions "that have certain desirable properties" it yet "does not show why these particular solutions should be especially significant" and, after all, "masks the possibility of steady waves" (Hunter 1972, p.234-35). Lynden-Bell admits that he "did not see how to translate our result into a real stability result on exp(it)modes with real or complex", referring to Drury (1980) as one who first "showed how to do this" (Lynden-Bell). However that may have been, sheared techniques adequately captured a very powerful amplification process, and this alone was to sound an alert to the danger of underrating them. Back.

¹¹ The reason why GLB neglected much simpler but sufficient "thin disk models with infinite density" is curious. They believed that those were "violently unstable since the growth rate of Jeans' gravitational instability is proportional to (G )^1/2" (GLB, p.127). Lynden-Bell disclosed the misthought once he had submitted the paper. Yet he did not disavow it by inserting corrections in proof: that would indicate an obvious inelegance of the authors' original analyses, and to reduce that would have meant to redo the whole publication because quite a number of its key discussions leaned principally on the vertical, third dimension.

Lynden-Bell to Toomre: "I have now read properly your work (Toomre 1964a) and write to apologize for our tirades against infinitely thin disks. Earlier we held the belief that because of the form of Jeans' instability formula all bodies of infinite density must be unstable with infinitely rapid growth rates and that analyses that only found finite rates were not really treating true Jeans instability but rather the associated divergence-free or incompressible oscillations of a compressible fluid. [...] I now agree that sufficiently anisotropic velocities can change the look of Jeans' criterion so that you are really discussing the same instabilities that we are." (Lynden-Bell 1964b)

"The centerpiece equation of GLB is more complicated than necessary because we did not clearly realize that it would have been adequate to study two-dimensional sheets. Thin disks faithfully capture all the horizontal dynamics of thick ones in the context of density wave theory and swing amplification. All of the regenerative spiral structure story could have been told in the context of two-dimensional disks because, aside from a minor correction for vertical thickness, all that matters for the dynamics is the horizontal velocity dispersion." (Goldreich) Back.

¹² To better understand the amplifying mechanism, GLB first looked into the situation with an infinite medium subjected at some moment to a slight disturbance in the plane of rotation, its gravity and pressure being turned off. Each elementary `fluid volume' there starts moving along its epicyclic orbit "with only one velocity at each point at any one time" (unlike its stellar counterpart with no oscillatory phase correlation of its stars), but as the epicyclic period changes with radius due to shear, the motions of `perturbed elements' on each given azimuth are progressively more and more out of phase, the stronger the larger is their separation, because of which the density amplitude in places grows with time. In the non-axisymmetric case, azimuthal phase (and amplitude) dependence of initial perturbed motions becomes one more growth factor: the shear brings parts with different phase and slightly different radius to a common azimuth, which only adds to the proportional phase-difference dependence on the radial distance and makes the density growth still stronger. But the same shear also produces a counteraction as it shortens trailing wavelengths thus reducing amplifying capacities. Overall, consequently, "this interesting behavior is not directly related to spiral arm formation." (GLB, p.130) Back.

¹³ "I suspect we didn't expend much effort attempting to provide a physical as opposed to a mathematical explanation for the transient growth of sheared waves." (Goldreich) Back.