


2.3. Spiral shock waves and induced star formation
Fujimoto, followed by Lin and Roberts, recognized that
gaseous motions generated by a tightly wrapped density wave
would be dominated by the appearance of tightly wrapped
shock waves. Later work
(Shu et al 1972)
has fulfilled Lin's
belief that the density wave itself might trigger star formation
and it is the shock that seems to be the trigger.
Lynden-Bell 1974,
p.117
It is not astonishing that one gets difficulties in making stars.
I think nature has difficulties too, because otherwise no inter-
stellar matter would be left.
Hoerner 1962, p.107
"In the early 1960s, Prendergast often expressed the view that the intense, slightly curving dust lanes seen within the bars of such SB galaxies as NGC 1300 and 5383 are probably the result of shocks in their contained gas, which he believed to be circulating in very elongated orbits. In such `geostrophic' flows of presumed interstellar clouds with random motions, Prendergast (1962, p.220) wrote that "it is not clear what is to be taken for an equation of state", but he knew that "we should expect a shock wave to intervene before the solution becomes multivalued". As regards the normal spirals, Lin and Shu (1964) stressed from the start that since the gas has relatively little pressure, its density contrast "may therefore be expected to be far larger than that in the stellar components" when exposed to a spiral force field such as they had just postulated. That hint remained largely dormant, however, until Fujimoto [...] combined these last two lines of thought" (Toomre 1977, p.453). 37
Fujimoto made his spiral-shock-wave report at the May 1966 IAU Symposium held in Burakan, Armenia, but it became widely known thanks to Prendergast. 38 He not only had urged Fujimoto to consider the problem and "helped much via fruitful discussion" (Fujimoto 1968, p.463), but also presented his results at Noordwijk, just three months after Burakan.
"Let us suppose one has a rotating system and a gravitational washboard, that is, a disturbance in the gravitational potential of a sinusoidal form. [...] Then what happens to the gas? [...] The answer is that the streamlines of the gas - instead of being straight lines, in this model corresponding to a perfect circular orbit - become somewhat cusped. In every cusp there is a shock; and in that shock the density increases, even for a very modest gravitational washboard, by an enormous factor; let us say five or more" (Prendergast 1967, p.310).
Fujimoto confirmed this shock-wave picture
(Fig.6) by computing
two-dimensional nonlinear dynamics of perfect isothermal gas in a
quasi-steady field of galactic spiral potential. As the spiral angular speed
"cannot be determined even by Lin's method", he decided to "take a priori
some reasonable values" and chose, as
Lindblad (1963) and
Kalnajs (1965)
did it, high speeds
 p
p
 45 km/sec/kpc and close
corotation
rc
45 km/sec/kpc and close
corotation
rc  5
kpc. The answer he gave was that "both the high-density
hydrogen gas contained in spiral arms and the dark lanes seen in external
galaxies on the concave side of their bright arms can be due to the presence
of the shock waves"
(Fujimoto 1968, p.463).
Lin reacted quickly and inspiringly. He assumed that a shock wave could
cause and organize star formation in the spiral arms
(Lin 1967b),
and posed as William
Roberts' thesis theme the problem of modeling "the presence of large-scale
`galactic shocks' that would be capable of triggering star formation in such
narrow spiral strips over the disk"
(Roberts 1969, p.124].
5
kpc. The answer he gave was that "both the high-density
hydrogen gas contained in spiral arms and the dark lanes seen in external
galaxies on the concave side of their bright arms can be due to the presence
of the shock waves"
(Fujimoto 1968, p.463).
Lin reacted quickly and inspiringly. He assumed that a shock wave could
cause and organize star formation in the spiral arms
(Lin 1967b),
and posed as William
Roberts' thesis theme the problem of modeling "the presence of large-scale
`galactic shocks' that would be capable of triggering star formation in such
narrow spiral strips over the disk"
(Roberts 1969, p.124].
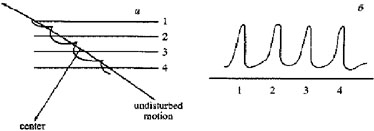 |
Figure 6. The behavior of interstellar gas in the spiral gravitational field of a galaxy, according to Fujimoto: (a) - the gas motion across the "gravitational washboard", (b) - the ensuing gas density distribution. (The figure is reproduced from Prendergast 1967) |
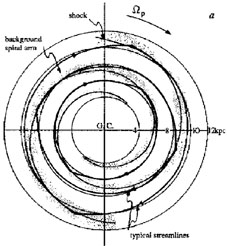
Roberts considerably developed and expanded Fujimoto's analyses. He corrected one mistake made by Fujimoto with his working equations (he had missed one of the full-value terms in the perturbed gas velocity equations), presented the star-disk potential description in the Lin-Shu asymptotic language, and focused on slowly rotating two-armed spirals with distant corotation. Roberts' interest was in a "particular type of solution of the nonlinear gas flow equations" permitting gas to pass through the shock waves coincident with spiral equipotential curves and describing the gas flow along a nearly concentric closed streamtube band, to exclude net radial transfer of anything. And indeed he got desirable solutions whose family presented "the composite gas flow picture over the whole galactic disk" (Roberts 1969, p.129). To this he conjectured that the shock wave, unaided by large-scale magnetic fields (which were Lin's initial candidate (Lin 1967b)), could trigger by itself the along-spiral formation of star associations.
"One might imagine that the gas in turbulent motion has `clouds' before the shock, which are on the verge of gravitational collapse; the sudden compression would then trigger off the collapse of the clouds, which would lead to star formation. After the gas left the shock region, it would again be decompressed, and the process of star formation would cease" (Lin et al 1969, p.737).
 |
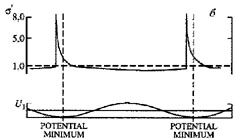 |
Figure 7. The behavior of interstellar gas in the spiral gravitational field of a galaxy, according to Roberts: (a) - a shock in the gas as its reaction to the spiral gravitational field of the stellar disk component, (b) - azimuthal density distributions in the stellar disk and interstellar gas. (The figures are reproduced from Roberts 1969) |
How could this sudden growth of the interstellar gas density and pressure trigger the desired gravitational collapse of the already existing dense clouds? Roberts did not know or show - he only said: conceivably (Roberts 1969, p.131) - but that hardly matters. 39 "The crucial point is that before the shock idea there had been no defensible explanation at all for the striking geometrical fact, first noticed by Baade in the late 1940s, that the main HII regions in large spirals tend to define considerably crisper and narrower arms than the rest of the visible material [...and that] these highly luminous chains seem biased toward the inner edges of arms, though perhaps not quite as much" (Toomre 1977, p.453-54). 40
Roberts' 1969 work was greatly appreciated as a basis for further studies of related problems in galaxy physics. Well familiar to astronomers in various contexts, the shock-wave idea in the new, spiral context appeared to many to be more attractive and soluble than the intricate collective effects from collisionless star-disk dynamics.
But there was some deserved criticism as well, largely in relation to Roberts' stress on closed gas streamlines. Pikelner (1970), who calculated energy loss of the gas as it crosses a spiral-wave arm and found it to be a few percent of its kinetic energy, concluded that in order that the gas might gradually come closer to center its streamlines had to be open. 41 He noticed also that "gas flows out of the arm slower than at the reversible compression, so that its mass center shifts behind the arm axis and pulls the stars ahead" (Pikelner 1970, p.758). Therefore, he inferred, angular momentum transfer from the shock-suffered gas to the spiral wave must amplify the latter, feeding it up with energy. Kalnajs corrected Pikelner in absentia (Simonson 1970; Kalnajs 1972). 42 Having established that the Lin-Shu slow waves carry over negative energy and momentum (Kalnajs 1971; Lynden-Bell & Kalnajs 1972), he recognized that their `pulling ahead' should cause the inverse effect, i.e. wave damping. All in all, the conclusion was that in open spirals (and bars, providing the general mass distribution in the SB-galaxies is also roughly axisymmetric) the shock wave "still more increases density and non-reversible dissipation of energy" (Pikelner 1970, p.758). "It meant not only that Roberts was slightly mistaken [...]. Much more important, this [...] implies that even the neatest spiral structures can at best be only quasi-steady" (Toomre 1977, p.460).
37 As such, the idea of a shock in the interstellar gas was not novel in the mid-1960s as for years it had helped various small-scale problems. So the larger-scale shock-wave speculation did not come to be very striking. Goldreich and Lynden-Bell (1965a, b), for instance, had it quietly on their spiral-regeneration concept. In fall 1964 Lynden-Bell remarked in his letter to Toomre, musing on the topics for their intended complementary work: "The other thing that is interesting is the formation of shock waves as the disturbances get very violently sheared, but while the overall structure of spiral arm formation is not very clear I would rather leave such a secondary problem till later" (Lynden-Bell 1964c). "I profess no vested interest in the formation of shock waves in an initially smooth gas layer, much against my upbringing as a fluid dynamicist, Toomre responded. All yours." (Toomre 1964d) "I am not going to work in shock waves for a few years yet, came Lynden-Bell's upright reaction, so you are welcome to them too." (Lynden-Bell 1964d) Back.
38 The Symposium proceedings were published in Russian 2.5 years later. Back.
39 "However, the previous discussions (Roberts 1969; Lin et al 1969) are incomplete - Shu and Roberts admitted. - There are severe difficulties in visualizing how this `effective pressure' is transmitted on a small scale to trigger the gravitational collapse of clouds since cloud-cloud collisions provide compression essentially only in one direction". Looking for "a clear physical basis for the mechanisms of the production of the shock and of the compression of the clouds", they discussed a two-phase model of the interstellar gas (Shu et al 1972, pp. 558, 585). Back.
40 "Two important assumptions underlie the above [Roberts'] gas dynamical results. The first is that the driving potential wave is tightly wound and the second that the interstellar medium can be adequately described as an isothermal gas. It is a great pity that these were introduced in the initial stages, since the results in many minds have been tightly associated with them. However, most of the results still stand if these assumptions are relaxed, e.g. it has been shown a number of times that a very open or even barred forcing can drive a similar response." (Athanassoula 1984, p.348) Back.
41 The latter factor, Pikelner noticed, "must have the cosmogonical consequence, [...] since in the lifetime of an Sc-galaxy gas must cross its [every] arm dozens of times. [...] Possibly, this explains why in spite of the intense star formation in galactic innermost parts there still remains a fair amount of gas." (Pikelner 1970, p.758). Back.
42 Kalnajs advanced his criticism in the course of a discussion at a special `Spiral Seminar' held in 1970 at the University of Maryland in connection with the problems of spiral structure as followed from the findings of the recent IAU Symposium at Basel, 1969 (see Simonson 1970). After, he discussed the subject corresponding with Roberts and then set it out in his special note (Kalnajs 1972). Shu and Roberts rejoined (Shu et al 1972; Roberts & Shu 1972). They agreed that, strictly speaking, gas streamlines could not be taken closed, but emphasized that in the WKBJ limit the actual non-closure per cycle was a quantity proportional to small spiral pitch angle, which Roberts reasonably neglected in his original paper. It must be said, however, that originally he was rather straightforward about following Lin's directive on a stationary picture (Lin 1967b, p.463), and in that way he even created some photogenic theory of gas `free modes' (Roberts 1969), which was really more than just asymptotic.
"Yup, these `free modes' happily lose energy, and keep on doing it forever without suffering any damage. This discovery deserves to be commercialized. [...] What is the secret that makes the streamlines closed? According to Appendix V [in the PhD thesis by Roberts (1968)], you just assume that in the equilibrium state there are axisymmetric radial and tangential forces." (Kalnajs)
For more detail on this discussion see Toomre 1977. Back.