4.2. Distinct cautions

Lin's programme for developing Lindblad's idea into a full
theory has up to now led to a theory of waves with neither a
convincing dynamical purpose nor a certain cause.
Lynden-Bell & Kalnajs 1972, p.25

All things considered, only cumbersome `global' mode analy-
ses and/or numerical experiments seem to offer any real hope
of completing the task of providing the wave idea of Lindblad
and Lin with the kind of firm deductive basis that one like to
associate with problems of dynamics.
Toomre 1977, p.452

Public acknowledgment of the Lin school was quite natural. Its initiative greatly helped in re-orienting astronomers toward active recognition of and observational tests for the gravitational nature and density-wave embodiment of large-scale spiral structure. No sooner had Lin adopted the QSSS hypothesis, he set himself the urgent and essential task of giving it adequate empirical support. The thing demanded a practicable analytical tool, and by 1966 he got it in a facile and handy asymptotic dispersion relation. That it explained neither the origin of spiral structure, nor the cause and mechanism for its tentatively long maintenance may well have worried Lin, but in consort with his original plan he relegated these kinds of topics to the future and rushed straight into empirical testing, having added some heavy claims to his available basics as if adequately backing the grand and quasi-steady spirals. Conveyed by him with the weight of his authority, this played an important part in turning the tide of the battle in his favor... and it affected the intuition, taste and attitude of his audience toward more fundamental aspects of the spiral problem.

Nonetheless, there were presentations at the Basel meeting that alerted its participants to the fact that true understanding of global spiral-making lay far beyond the asymptotic theory they applauded and was bound to take quite a while longer. One of the cautions came from Kalnajs (1970) in connection with his long-term theme of coupled epicyclic oscillations of stars in a thin disk.

Lindblad had introduced and studied the test-star-studded narrow rings - `dispersion orbits'. Kalnajs (1965) in his thesis examined their gravitational coupling, first in pairs <sup>65</sup> and then in the whole, already in a continuous disk setting. There he derived an integral equation for his disk's oscillatory dynamics, <sup>66,67</sup> and in Basel he demonstrated a variant of its numerical solution. That was a trailing bar-spiral mode m = 2 with an e-fold growth in about two rotational periods of the outer disk (Fig.13a). Kalnajs was pretty sure that his analysis already resolved much of the global spiral-mode problem, and he believed that at least qualitative confrontation with the evidence would prove successful. In this respect he attached particular importance to the fact that his analyzed gas-component reaction to the forming mode showed a tightly wrapped two-armed spiral (Fig.13b). It was, however, far from certain why his main unstable mode could not grow faster and how, even at rather moderate growth rates, it would help one for very long. But anyway that cast no doubt on Kalnajs' principal result - the strong tendency of a star disk to develop a temporary open two-armed spiral structure, which in turn encourages bar-formation. Thus the Schmidt model of our Galaxy, which was more or less favored in the 1960s by various investigators and which Kalnajs now checked, was seriously unstable and unsatisfactory. If true, this alone would soon overwhelm any `self-sustained modes' of Lin and Shu peacefully revolving in a disk of stars.

Figure 13. Kalnajs' growing bar mode: excess densities (a) in the stellar disk, (b) in its gas layer. Large and small circles mark the outer Lindblad and corotation resonances, point S - Sun's position. (The figure is reproduced from Kalnajs 1970)

Another caution came in Basel from the evidence provided by numerical experiments. First computer simulations of the flat-galaxy dynamics as the N -body problem had been performed in the late 1950s by P.O. Lindblad (1962). He then took about 200 points only, because the early electronic computer was painfully slow on direct calculation of paired interactions for appreciably higher N's. This stimulated new approaches to numerical experiments, and by 1968 Kevin Prendergast and Richard Miller worked out a more effective scheme which, calculating forces in a limited number of cells, allowed rather quick and accurate dynamical description of as much as 10⁵particles or so. ⁶⁸ Inspired with the observation that "because the program is new, new results are coming rapidly" (Prendergast & Miller 1968, p.705), they and William Quirk prepared for Basel a motion picture of "the very interesting physical implications" of their experiments (Miller et al 1970a, b). Spectacular spiral patterns were found to "nearly always develop [already] in the early stages" of their model disks, yet - they argued - these "cannot be valid N -body analogues of the spiral patterns of actual galaxies" as most evidently reflecting violent reorganization of the artificially arranged initial state. More importantly, it was ascertained that "machine calculations typically produce `hot' systems that are largely pressure-supported" (Miller et al 1970b, p.903-4), in contrast to the observed thin disks in galaxies.

The above experimenters found a simple but interesting way out - a `manual' cooling "by appropriately modifying the systems already in the computer" (Miller et al 1970b, p.904). By integration steps (cycles) they cooled some 10% of their particles, preserving their orbital momentum to imitate their inelastic mutual collisions and make them dynamically akin to interstellar gas clouds. As before, the remaining 90% heated up to the circular-speed-comparable velocity dispersions, but with this a bar was formed and also a trailing pattern of moderate winding that, although chaotic and flexible as it might appear as a whole, contained a bar-bound m = 2 spiral wave component (Fig.14). Slowly revolving in the sense of general flow, the bar and the gradually tightening spiral faded from the sight in about three disk rotations.

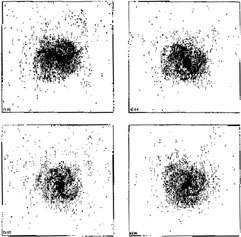Figure 14. The formation and evolution of the bar-spiral structure in a partially cooled gravitating disk. (The frames are reproduced from Miller et al 1970)

Frank Hohl and Roger Hockney worked out a more accurate computational scheme in the late 1960s (Hockney & Hohl 1969). Unlike Prendergast and coworkers, Hohl's interest lay in `pure' dynamics of collisionless models. <sup>69</sup> In Basel he experimentally confirmed the fact of fast - for a period of one revolution - small-scale fragmentation of cold star disks and its prevention by a massive (no less than four disk masses) spherical halo (Hohl 1970a). The hot disks were checked separately (Hohl 1971) to get stable in Toomre's axisymmetric sense at the initial `temperature' Q = 1, but then they still remained unstable against relatively slowly growing large-scale disturbances that caused the system to assume a very pronounced bar-shaped structure after two rotations (Fig.15); ⁷⁰ in major features it confirmed the growing bar-spiral mode picture that Kalnajs (1970) had obtained via his integral equation. The total lack of spiral shapes of respectable duration in this and every other purely stellar-dynamical experiment conducted with sizable fractions of `mobile' mass was a result that almost spoke for itself. ⁷¹ Indeed, just like the modal work of Kalnajs and the N-body results of Prendergast et alia, it cautioned everyone at Basel that this strong tendency toward bar-making very much needed to be understood and tamed lest it overwhelm the QSSS hopes of Lin and all his admirers.

Figure 15. The evolution of a stellar disk from an initially balanced state of uniform rotation and marginal stability Q = 1. Time is in initial rotation period units. (The figure is reproduced from Hohl 1971)

⁶⁵ Kalnajs considered a pair of rings separated by a corotation region. He found that each of them is corresponded by two basic oscillatory modes, one fast and the other slow, and that even in axisymmetrically stable situations the different-type mode coupling creates instability causing an outward angular momentum transfer. Yet on this fact "it would be premature to draw any conclusions about spiral arms of galaxies", he judged (Kalnajs 1965, p.81). "By that time I knew about the shearing sheet results. The two-ring example works even more accurately in this setting. But of course one knows that the sheet is stable and therefore the results inferred from two rings are not the same as that from 2N rings - of mass proportional to 1/N - when one lets N go to infinity." (Kalnajs) Back.

⁶⁶ To reduce his complex integral equation, Kalnajs limited its frequency range by specifying angular momentum radial distribution. He took Lindblad's - / 2 const for the main part of a flat galaxy and the Keplerian for its outer part, thus imitating (or implying) an `edge' in his galactic system. As in the case of paired rings, two modes, slow and fast, grew prevalent, the first one contributing much more. This enabled Kalnajs to describe the modes separately and then account for their coupling by perturbation theory methods. The kernel of the slow-mode equation revealed no pole, it was symmetrical, and the mode stable and devoid of trailing or leading signs. But the kernel of the fast-mode equation had a pole at the OLR associated with the said `edge'. This changed the qualitative situation: interacting with the OLR, the relatively slowly growing perturbations supported the trailing character of the fast mode and, therefore, of the entire spiral wave. Back.

⁶⁷ (Contopoulos): "Kalnajs' thesis has a correct remark about trailing waves in a particular page. I copied it and asked Toomre whether he could find there the preference of trailing waves, but he couldn't. This convinced me that I should publish my own results."

(Toomre): "I have no such memory, but this is in no way to dispute George's own recollection. [...] He always strove to be very fair to Agris as a significant independent worker who had many good ideas and sound mathematics. And so it is entirely plausible that he asked me whether I thought that Agris - then still lacking any true global-mode results that his thesis had been struggling to develop - had really clinched that all realistic spirals must trail. Indeed, I remain pretty sure that Agris by then had not done so ...but ask him yourself!"

(Kalnajs): "Unlike most people who would prefer a physical (or verbal) explanation, George was keen to see the mathematics behind the leading/trailing preference. Fortunately there is a simple enough approximation of the galactic parameters in the vicinity of an OLR whose contribution to the integral equation can be evaluated in closed form. The result is eqn (117) of my thesis. In the subsequent three pages I explained how that contribution to the kernel changes from one that in the absence of a resonance does not favor leading over trailing, to one that prefers trailing waves when a resonance is present. [...] Today I would use a simpler example, perhaps the shearing sheet." Back.

⁶⁸ Following Miller & Prendergast (1968), particles `jumped' between discrete-valued locations and velocities under discrete forces. The fast finite Fourier-transform method was used for solving Poisson's equation at each integration step. Back.

⁶⁹ To avoid computational artifacts, Hohl had carefully examined properties of his numerical schemes and showed that his N -body models were indeed collisionless (Hohl 1973) and their behavior was independent of the particle number, cell size and integration time step (Hohl 1970b). Back.

⁷⁰ In two more rotations, a nearly axisymmetric distribution of stars around a massive central oval resulted, revolving about half as fast as the initial disk. Back.

⁷¹ "It is conceivable, of course, that some milder instabilities which might themselves have led to more enduring spirals, were thwarted in these experiments by a kind of overheating from the fierce initial behavior. This seems unlikely, however, because of Hohl's extra tests with that artificial cooling (Hohl 1971)." (Toomre 1977, p.468) Back.