4.2. Photometric Redshifts

Lyman-break and Lyman-forest methods are just two examples of photometric redshift determinations, in which galaxy redshifts are estimated using multiband photometric information. The idea has a long history, dating back to Baum (1962) who used nine-band photoelectric data to estimate galaxy cluster redshifts. Koo (1985), analyzing four-band photographic data, showed that isoredshift contours on color-color plots provide reliable photometric redshift estimates. Recently, photometric techniques have enjoyed a revival, largely catalyzed by the deep photometry of the HDF and the new generation of large-format CCD arrays. The typical redshift uncertainty for the photometric methods is expected to be in the range of z = 0.05-0.10. This accuracy is sufficient for many scientific goals, such as luminosity function determinations, luminosity density determinations, and projected correlation function analyses. The technique is also efficient for identifying unusual sources, such as distant galaxies, quasars, and galaxy clusters, which can then be targeted for detailed spectroscopic study.

Several teams are actively pursuing photometric redshift determinations, and the HDF (recently augmented by the HDF-South) has been an excellent laboratory for validating the technique (cf. Hogg et al. 1998). Table 3 lists some of the primary working groups with brief commentary on their technique. Figure 6, comparing spectroscopic redshifts in the HDF with photometric redshift determinations by the Stony Brook group, illustrates the robustness of photometric redshift determinations. A recent review of photometric redshifts is presented in Yee (1998).

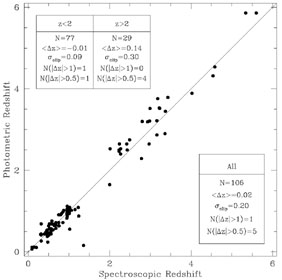Figure 6. A comparison of spectroscopic and photometric redshifts in the (Northern) HDF. Photometric redshifts are from the Stony Brook group, as detailed in the text. Spectroscopic redshifts are from the literature. Insets indicate various comparisons between the redshift determinations in two redshift bins as well as the entire sample: N is the number of galaxies, <z> is the average difference between zspec and zphot, clip is the clipped dispersion between the measurements, and N(|z| > 0.5, 1) measures the number of outlier photometric redshift determinations. Although this plot reports solely on the Stony Brook photometric redshift determinations, dispersions of 0.2 between zspec and zphot are typical of many of the successful photometric redshift measurements in the HDF. Figure courtesy Fernàndez-Soto et al. (1999).

Contemporary photometric redshift determinations can be divided into two major strategies. The first approach (e.g., Koo 1985; Lanzetta, Yahil, & Fernàndez-Soto 1996; Gwyn & Hartwick 1996; Mobasher et al. 1996; Sawicki, Lin, & Yee 1997; Benítez 1999; Fernàndez-Soto, Lanzetta, & Yahil 1999) involves fitting observed galaxy colors with redshifted spectral templates. These templates may be empirical, synthetic, or hybrid, and may be modified by dust absorption and/or the redshift-dependent opacity of intergalactic hydrogen. Statistical treatments are used to determine a redshift distribution function, generally quoted as a single number corresponding to the peak of the distribution. However, determinations of, for example, galaxy luminosity functions, should retain the photometric redshift distribution function to reliably indicate the uncertainties of the analysis. The other approach (e.g., Connolly et al. 1995, 1997; Brunner et al. 1997; Wang, Bahcall, & Turner 1998) is purely empirical: with a sufficiently large training set, an empirical relation between redshift and observed magnitudes m₀ and colors C can be determined, z = z(m₀, C).

We detail the method used by the Stony Brook group (Lanzetta et al. 1996; Fernàndez-Soto et al. 1999) to give some flavor of photometric redshift determinations. They begin with the four empirical galaxy spectral energy distributions of Coleman, Wu, & Weedman (1980), corresponding to four observed galaxy types (E/S0, Sbc, Scd, and Irr) and covering the wavelength range 1400-10000 Å. The templates are extrapolated in the UV to 912 Å using the empirical spectra of Kinney et al. (1993), and are extrapolated in the infrared to 25 µm using the spectral evolutionary models of Bruzual & Charlot (1993). The hybrid templates are redshifted and the redshift-dependent UV hydrogen absorptions are removed using a model of the optical depth of hydrogen. At modest redshift, this transmission function is empirically derived from observations of quasars (e.g., Madau 1995). The shifted, absorbed spectra are then convolved with the transmission curves of the relevant filters and a redshift likelihood function is calculated relating the model colors to measured fluxes. Comparisons between photometric and spectroscopic redshift determinations in the HDF show that the former is typically robust to z 0.34 for objects with I₈₁₄ ~ 25.5 and z > 3. Residuals are typically z_rms / (1 + z) 0.1 at all redshifts (see Fig. 6).

Other template photometric redshift estimates generally vary in only two considerations: (1) the input spectral templates and (2) the method of determining the best-fit z_phot. Input spectral templates may be purely empirical, purely synthetic, or hybrid as in the Stony Brook analysis (see Table 3). Input libraries may also vary in the number of templates. Many groups use the four empirical spectral energy distributions of Coleman et al. (1980). The addition of one or more star-forming galaxy templates, as assembled by Calzetti, Kinney, & Storchi-Bergmann (1994), has been noted to improve the accuracy of the photometric redshift determination by some groups. Determination of the best-fit z_phot relies on a statistical analysis. For example, the Stony Brook group uses a maximum likelihood analysis, while Benítez (1999) applies Bayesian marginalization and prior probabilities to the problem.

The training set method has the advantage of being purely empirical, and therefore not relying on a choice of input templates. However, the weakness is that the method requires and is dependent upon a large and accurate input training set. Redshift ranges with sparse numbers of confirmed redshifts, such as 1 z 2.5 and z 4, lead to poorly determined photometric redshift determinations. The various practitioners of this technique vary in the degree polynomial used to fit the multivariate function z = z(m₀, C) and whether or not they implement observed flux as a variable in the optimal fit.

In terms of the current review on search techniques for protogalaxies, we are most interested in the robustness of these photometric procedures in identifying the high-redshift (z 4) tail in the field galaxy redshift distribution. Fernàndez-Soto et al. (1999) find five galaxies brighter than I₈₁₄ = 26.5 in the HDF with 4.5 < z < 5.5, corresponding to a surface density of 1.0 galaxies arcmin^-2 (unit-z)^-1 at z = 5. Spectroscopic confirmation of the high-redshift photometric candidates is necessary to validate the technique before photometric redshift measurements of, for example, the star formation history of the early universe are well established. Over the past 3 years, our Berkeley-based group has been using slit masks with the Low Resolution Imaging Spectrometer (LRIS; Oke et al. 1995) on the Keck II telescope to measure faint galaxy spectra in the HDF. We choose z 4 candidates in collaboration with the Stony Brook-based photometric redshift group. With the current instrumentation, spectroscopic redshift measurements are viable perhaps to I₈₁₄ 27.5 for emission-line sources and to I₈₁₄ 26 for objects without strong emission lines. But even at I₈₁₄ 25.5, the effort is fairly "heroic": observations of a single faint galaxy can easily extend over multiple observing seasons in order to measure a reliable spectroscopic redshift. Figure 7 presents Keck/LRIS spectra of three high-redshift sources in the HDF obtained by our Berkeley-based group. In Table 4 we list a comparison of spectroscopic and photometric redshifts for galaxies in the HDF at z > 4.

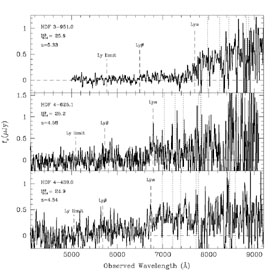Figure 7. Keck/LRIS spectra of HDF 3-951.0, HDF 4-625.0, and HDF 4-439.0, three photometrically selected high-redshift galaxies in the HDF. The spectrum of HDF 3-951.0 represents 6 hr of integration with the 150/7500 lines mm-1 grating, significantly more sensitive than the discovery spectrogram presented in Spinrad et al. (1998). The slightly revised redshift of z = 5.33 is based on the Ly discontinuity, which is located at a wavelength less affected by telluric emission than the Ly discontinuity. The spectra of HDF 4-625.0 and represent sums of data from multiple observing seasons. Vertical dotted lines indicate the location of absorption lines typically observed in Lyman-break galaxies at z 3.

Table 4. Spectroscopic vs. Photometric Redshifts in the HDF at z > 4

Galaxy	zspec	zphot	WLyobs (Å)	I814 (AB) (mag)	Reference
HDF 3-512.0...	4.02	3.56	200	25.5	1
HDF 4-439.0...	4.54	4.32	~ 20	24.9	2
HDF 4-625.0...	4.58	4.52	~ 100	25.2	2
HDF 3-951.0...	5.33	5.72	...	25.6	3
HDF 4-473.0...	5.60	5.64	~ 300	27.1	4
NOTES. - Photometric redshift zphot from Fernàndez-Soto et al. 1999. I814 magnitude from Williams et al. 1996. References. - (1) Dickinson 1998; (2) Stern et al. 2000; (3) Spinrad et al. 1998; (4) Weymann et al. 1998.