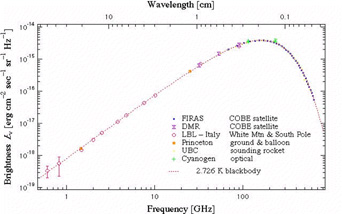
The CBR is the most perfect blackbody ever seen, according to the FIRAS (Far InfraRed Absolute Spectrometer) instrument of COBE, which measured a temperature of T0 = 2.726 ± 0.010 K (Mather et al., 1994). The theoretical prediction that the CBR will have a blackbody spectrum appears to be confirmed by the FIRAS observation (see Figure 1). But this is not the end of the story. FIRAS only observed the peak of the blackbody. Other experiments have mapped out the Rayleigh-Jeans part of the spectrum at low frequency. Most are consistent with a 2.73 K blackbody, but some are not. It is in the low-frequency limit that the greatest spectral distortions might occur because a Bose-Einstein distribution differs from a Planck distribution there. However, double Compton and bremsstrahlung are most effective at low frequencies so strong deviations from a blackbody spectrum are not generally expected.
|
Figure 1. Measurements of the CMB spectrum. |
Spectral distortions in the Wien tail of the spectrum are quite difficult to detect due to the foreground signal from interstellar dust at those high frequencies. For example, broad emission lines from electron capture at recombination are predicted in the Wien tail but cannot be distinguished due to foreground contamination (White et al., 1994). However, because the energy generated by star formation and active galactic nuclei is absorbed by interstellar dust in all galaxies and then re-radiated in the far-infrared, we expect to see an isotropic Far-Infrared Background (FIRB) which dominates the CMB at frequencies above a few hundred GHz. This FIRB has now been detected in FIRAS data (Puget et al., 1996; Fixsen et al., 1998; Burigana & Popa, 1998) and in data from the COBE DIRBE instrument (Dwek et al., 1998; Schlegel et al., 1998).
Although Compton, double Compton, and bremsstrahlung interactions occur frequently until decoupling, the complex interplay between them required to thermalize the CBR spectrum is ineffective at redshifts below 107. This means that any process after that time which adds a significant portion of energy to the universe will lead to a spectral distortion today. Neutrino decays during this epoch should lead to a Bose-Einstein rather than a Planck distribution, and this allows the FIRAS observations to set constraints on the decay of neutrinos and other particles in the early universe (Kolb & Turner, 1990). The apparent impossibility of thermalizing radiation at low redshift makes the blackbody nature of the CBR strong evidence that it did originate in the early universe and as a result serves to support the Big Bang theory.
The process of Compton scattering can cause spectral distortions if it is too late for double Compton and bremsstrahlung to be effective. In general, low-frequency photons will be shifted to higher frequencies, thereby decreasing the number of photons in the Rayleigh-Jeans region and enhancing the Wien tail. This is referred to as a Compton-y distortion and it is described by the parameter
 |
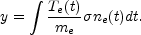(5) |
The apparent temperature drop in the long-wavelength limit is
 |
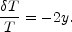(6) |
The most important example of this is Compton scattering of photons off
hot electrons in galaxy clusters, called the Sunyaev-Zel'dovich (SZ)
effect. The electrons transfer energy to the photons, and the spectral
distortion results from the sum of all of the scatterings off
electrons in
thermal motion, each of which has a Doppler shift. The
SZ effect from clusters can yield a distortion of
y 
10-5 - 10-3 and these distortions have been
observed in several rich clusters of galaxies. The FIRAS observations place
a constraint on any full-sky Comptonization by limiting the average
y-distortion to y < 2.5 × 10-5
(Hu, 1995).
The integrated y-distortion predicted from the SZ effect of
galaxy clusters and large-scale structure is over a factor of ten lower
than this observational constraint
(Refregier et
al., 1998)
but that from "cocoons" of radio galaxies
(Yamada et al.,
1999)
is predicted to be of the same order. A kinematic SZ effect is caused by
the bulk velocity of the cluster; this is a small effect which is very
difficult to detect for individual clusters but will likely
be measured statistically by the Planck satellite.