4. COSMIC MICROWAVE BACKGROUND ANISOTROPY OBSERVATIONS

Since the COBE DMR detection of CMB anisotropy (Smoot et al., 1992), there have been over thirty additional measurements of anisotropy on angular scales ranging from 7° to 0.°3, and upper limits have been set on smaller scales.

The COBE DMR observations were pixelized into a skymap, from which it is possible to analyze any particular multipole within the resolution of the DMR. Current small angular scale CMB anisotropy observations are insensitive to both high and low multipoles because they cannot measure features smaller than their resolution and are insensitive to features larger than the size of the patch of sky observed. The next satellite mission, NASA's Microwave Anisotropy Probe (MAP), is scheduled for launch in Fall 2000 and will map angular scales down to 0.°2 with high precision over most of the sky. An even more precise satellite, ESA's Planck, is scheduled for launch in 2007. Because COBE observed such large angles, the DMR data can only constrain the amplitude A and index n of the primordial power spectrum in wave number k, P_p(k) = Akⁿ, and these constraints are not tight enough to rule out very many classes of cosmological models.

Until the next satellite is flown, the promise of microwave background anisotropy measurements to measure cosmological parameters rests with a series of ground-based and balloon-borne anisotropy instruments which have already published results (shown in Figure 4) or will report results in the next few years (MAXIMA, BOOMERANG, TOPHAT, ACE, MAT, VSA, CBI, DASI, see Lee et al., 1999 and Halpern & Scott, 1999). Because they are not satellites, these instruments face the problems of shorter observing times and less sky coverage, although significant progress has been made in those areas. They fall into three categories: high-altitude balloons, interferometers, and other ground-based instruments. Past, present, and future balloon-borne instruments are FIRS, MAX, MSAM, ARGO, BAM, MAXIMA, QMAP, HACME, BOOMERANG, TOPHAT, and ACE. Ground-based interferometers include CAT, JBIAC, SUZIE, BIMA, ATCA, VLA, VSA, CBI, and DASI, and other ground-based instruments are TENERIFE, SP, PYTHON, SK, OVRO/RING, VIPER, MAT/TOCO, IACB, and WD. Taken as a whole, they have the potential to yield very useful measurements of the radiation power spectrum of the CMB on degree and subdegree scales. Ground-based non-interferometers have to discard a large fraction of data and undergo careful further data reduction to eliminate atmospheric contamination. Balloon-based instruments need to keep a careful record of their pointing to reconstruct it during data analysis. Interferometers may be the most promising technique at present but they are the least developed, and most instruments are at radio frequencies and have very narrow frequency coverage, making foreground contamination a major concern. In order to use small-scale CMB anisotropy measurements to constrain cosmological models we need to be confident of their validity and to trust the error bars. This will allow us to discard badly contaminated data and to give greater weight to the more precise measurements in fitting models. Correlated noise is a great concern for instruments which lack a rapid chopping because the 1/f noise causes correlations on scales larger than the beam in a way that can easily mimic CMB anisotropies. Additional issues are sample variance caused by the combination of cosmic variance and limited sky coverage and foreground contamination.

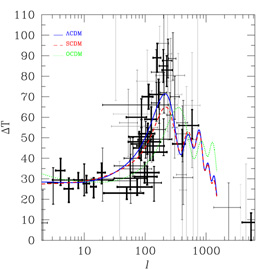Figure 4. Compilation of CMB Anisotropy observations. Vertical error bars represent 1 uncertainties and horizontal error bars show the range from min to max of Table 1. The line thickness is inversely proportional to the variance of each measurement, emphasizing the tighter constraints. All three models are consistent with the upper limits at the far right, but the Open CDM model (dotted) is a poor fit to the data, which prefer models with an acoustic peak near = 200 with an amplitude close to that of CDM (solid).

Table 1. Complete compilation of CMB anisotropy observations 1992-1999, with maximum likelihood T, upper and lower 1 uncertainties (not including calibration uncertainty), the weighted center of the window function, the values where the window function falls to e^-1/2 of its maximum value, the 1 calibration uncertainty, and references given below.

Instrument	T (µK)	+ 1(µK)	- 1(µK)	eff	min	max	1 cal.	ref.
COBE1	8.5	16.0	8.5	2.1	2	2.5	0.7	1
COBE2	28.0	7.4	10.4	3.1	2.5	3.7	0.7	1
COBE3	34.0	5.9	7.2	4.1	3.4	4.8	0.7	1
COBE4	25.1	5.2	6.6	5.6	4.7	6.6	0.7	1
COBE5	29.4	3.6	4.1	8.0	6.8	9.3	0.7	1
COBE6	27.7	3.9	4.5	10.9	9.7	12.2	0.7	1
COBE7	26.1	4.4	5.3	14.3	12.8	15.7	0.7	1
COBE8	33.0	4.6	5.4	19.4	16.6	22.1	0.7	1
FIRS	29.4	7.8	7.7	10	3	30	-a	2
TENERIFE	30	15	11	20	13	31	-a	3
IACB1	111.9	49.1	43.7	33	20	57	20	4
IACB2	57.3	16.4	16.4	53	38	75	20	4
SP91	30.2	8.9	5.5	57	31	106	15	5
SP94	36.3	13.6	6.1	57	31	106	15	5
BAM	55.6	27.4	9.8	74	28	97	20	6
ARGO94	33	5	5	98	60	168	5	7
ARGO96	48	7	6	109	53	179	10	8
JBIAC	43	13	12	109	90	128	6.6	9
QMAP(Ka1)	47.0	6	7	80	60	101	12	10
QMAP(Ka2)	59.0	6	7	126	99	153	12	10
QMAP(Q)	52.0	5	5	111	79	143	12	10
MAX234	46	7	7	120	73	205	10	11
MAX5	43	8	4	135	81	227	10	12
MSAMI	34.8	15	11	84	39	130	5	13
MSAMII	49.3	10	8	201	131	283	5	13
MSAMIII	47.0	7	6	407	284	453	5	13
PYTHON123	60	9	5	87	49	105	20	14
PYTHON3S	66	11	9	170	120	239	20	14
PYTHONV1	23	3	3	50	21	94	17b	15
PYTHONV2	26	4	4	74	35	130	17	15
PYTHONV3	31	5	4	108	67	157	17	15
PYTHONV4	28	8	9	140	99	185	17	15
PYTHONV5	54	10	11	172	132	215	17	15
PYTHONV6	96	15	15	203	164	244	17	15
PYTHONV7	91	32	38	233	195	273	17	15
PYTHONV8	0	91	0	264	227	303	17	15
SK1c	50.5	8.4	5.3	87	58	126	11	16
SK2	71.1	7.4	6.3	166	123	196	11	16
SK3	87.6	10.5	8.4	237	196	266	11	16
SK4	88.6	12.6	10.5	286	248	310	11	16
SK5	71.1	20.0	29.4	349	308	393	11	16
TOCO971	40	10	9	63	45	81	10	17
TOCO972	45	7	6	86	64	102	10	17
TOCO973	70	6	6	114	90	134	10	17
TOCO974	89	7	7	158	135	180	10	17
TOCO975	85	8	8	199	170	237	10	17
TOCO981	55	18	17	128	102	161	8	18
TOCO982	82	11	11	152	126	190	8	18
TOCO983	83	7	8	226	189	282	8	18
TOCO984	70	10	11	306	262	365	8	18
TOCO985	24.5	26.5	24.5	409	367	474	8	18
VIPER1	61.6	31.1	21.3	108	30	229	8	19
VIPER2	77.6	26.8	19.1	173	72	287	8	19
VIPER3	66.0	24.4	17.2	237	126	336	8	19
VIPER4	80.4	18.0	14.2	263	150	448	8	19
VIPER5	30.6	13.6	13.2	422	291	604	8	19
VIPER6	65.8	25.7	24.9	589	448	796	8	19
BOOM971	29	13	11	58	25	75	8.1	20
BOOM972	49	9	9	102	76	125	8.1	20
BOOM973	67	10	9	153	126	175	8.1	20
BOOM974	72	10	10	204	176	225	8.1	20
BOOM975	61	11	12	255	226	275	8.1	20
BOOM976	55	14	15	305	276	325	8.1	20
BOOM977	32	13	22	403	326	475	8.1	20
BOOM978	0	130	0	729	476	1125	8.1	20
CAT96I	51.9	13.7	13.7	410	330	500	10	21
CAT96II	49.1	19.1	13.7	590	500	680	10	21
CAT99I	57.3	10.9	13.7	422	330	500	10	22
CAT99II	0.	54.6	0.	615	500	680	10	22
OVRO/RING	56.0	7.7	6.5	589	361	756	4.3	23
HACME	0.	38.5	0.	38	18	63	-a	29
WD	0.	75.0	0.	477	297	825	30	24
SuZIE	16	12	16	2340	1330	3070	8	25
VLA	0.	27.3	0.	3677	2090	5761	-a	26
ATCA	0.	37.2	0.	4520	3500	5780	-a	27
BIMA	8.7	4.6	8.7	5470	3900	7900	-a	28
REFERENCES: 1- Kogut et al. (1996a); Tegmark & Hamilton (1997) 2- Ganga et al. (1994) 3- Gutierrez et al. (1999) 4- Femenia et al. (1998) 5- Ganga et al. (1997b); Gundersen et al. (1995) 6- Tucker et al. (1997) 7- Ratra et al. (1999) 8- Masi et al. (1996) 9- Dicker et al. (1999) 10- De Oliveira-Costa et al. (1998) 11- Clapp et al. (1994); Tanaka et al. (1996) 12- Ganga et al. (1998) 13- Wilson et al. (1999) 14- Platt et al. (1997) 15- Coble et al. (1999) 16- Netterfield et al. (1997) 17- Torbet et al. (1999) 18- Miller et al. (1999) 19- Peterson et al. (1999) 20- Mauskopf et al. (1999) 21- Scott et al. (1996) 22- Baker et al. (1999) 23- Leitch et al. (1998) 24- Ratra et al. (1998) 25- Church et al. (1997); Ganga et al. (1997a) 26- Partridge et al. (1997) 27- Subrahmanyan et al. (1993) 28- Holzapfel et al. (1999) 29- Staren et al. (1999) a Could not be determined from the literature. b Results from combining the +15% and -12% calibration uncertainty with the 3µK beamwidth uncertainty. The non-calibration errors on the PYTHONV datapoints are highly correlated. c The SK T and error bars have been re-calibrated according to the 5% increase recommended by Mason et al. (1999) and the 2% decrease in T due to foreground contamination found by De Oliveira-Costa et al. (1997).

Figure 4 shows our compilation of CMB anisotropy observations without adding any theoretical curves to bias the eye ². It is clear that a straight line is a poor but not implausible fit to the data. There is a clear rise around = 100 and then a drop by = 1000. This is not yet good enough to give a clear determination of the curvature of the universe, let alone fit several cosmological parameters. However, the current data prefer adiabatic structure formation models over isocurvature models (Gawiser & Silk, 1998). If analysis is restricted to adiabatic CDM models, a value of the total density near critical is preferred (Dodelson & Knox, 1999).

4.1. Window Functions

The sensitivity of these instruments to various multipoles is called their window function. These window functions are important in analyzing anisotropy measurements because the small-scale experiments do not measure enough of the sky to produce skymaps like COBE. Rather they yield a few "band-power" measurements of rms temperature anisotropy which reflect a convolution over the range of multipoles contained in the window function of each band. Some instruments can produce limited skymaps (White & Bunn, 1995). The window function W shows how the total power observed is sensitive to the anisotropy on the sky as a function of angular scale:

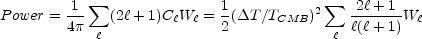(13)

where the COBE normalization is T = 27.9 µK and T_CMB = 2.73 K (Bennett et al., 1996). This allows the observations of broad-band power to be reported as observations of T, and knowing the window function of an instrument one can turn the predicted C spectrum of a model into the corresponding prediction for T. This "band-power" measurement is based on the standard definition that for a "flat" power spectrum, T = (( + 1) C)^1/2 T_CMB / (2) (flat actually means that ( + 1) C is constant).

The autocorrelation function for measured temperature anisotropies is a convolution of the true expectation values for the anisotropies and the window function. Thus we have (White & Srednicki, 1995)

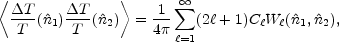(14)

where the symmetric beam shape that is typically assumed makes W a function of separation angle only. In general, the window function results from a combination of the directional response of the antenna, the beam position as a function of time, and the weighting of each part of the beam trajectory in producing a temperature measurement (White & Srednicki, 1995). Strictly speaking, W is the diagonal part of a filter function W _' that reflects the coupling of various multipoles due to the non-orthogonality of the spherical harmonics on a cut sky and the observing strategy of the instrument (Knox, 1999). It is standard to assume a Gaussian beam response of width , leading to a window function

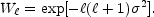(15)

The low- cutoff introduced by a 2-beam differencing setup comes from the window function (White et al., 1994)

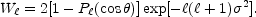(16)

4.2. Sample and Cosmic Variance

The multipoles C can be related to the expected value of the spherical harmonic coefficients by

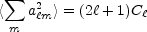(17)

since there are (2 + 1) a_m for each and each has an expected autocorrelation of C. In a theory such as inflation, the temperature fluctuations follow a Gaussian distribution about these expected ensemble averages. This makes the a_m Gaussian random variables, resulting in a ²₂₊₁ distribution for _m a_m². The width of this distribution leads to a cosmic variance in the estimated C of _cv² = ( + 1/2)^-1/2 C, which is much greater for small than for large (unless C is rising in a manner highly inconsistent with theoretical expectations). So, although cosmic variance is an unavoidable source of error for anisotropy measurements, it is much less of a problem for small scales than for COBE.

Despite our conclusion that cosmic variance is a greater concern on large angular scales, Figure 4 shows a tremendous variation in the level of anisotropy measured by small-scale experiments. Is this evidence for a non-Gaussian cosmological model such as topological defects? Does it mean we cannot trust the data? Neither conclusion is justified (although both could be correct) because we do in fact expect a wide variation among these measurements due to their coverage of a very small portion of the sky. Just as it is difficult to measure the C with only a few a_m, it is challenging to use a small piece of the sky to measure multipoles whose spherical harmonics cover the sphere. It turns out that limited sky coverage leads to a sample variance for a particular multipole related to the cosmic variance for any value of by the simple formula

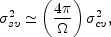(18)

where is the solid angle observed (Scott et al., 1994). One caveat: in testing cosmological models, this cosmic and sample variance should be derived from the C of the model, not the observed value of the data. The difference is typically small but will bias the analysis of forthcoming high-precision observations if cosmic and sample variance are not handled properly.

4.3. Binning CMB data

Because there are so many measurements and the most important ones have the smallest error bars, it is preferable to plot the data in some way that avoids having the least precise measurements dominate the plot. Quantitative analyses should weight each datapoint by the inverse of its variance. Binning the data can be useful for display purposes but is dangerous for analysis, because a statistical analysis performed on the binned datapoints will give different results from one performed on the raw data. The distribution of the binned errors is non-Gaussian even if the original points had Gaussian errors. Binning might improve a quantitative analysis if the points at a particular angular scale showed a scatter larger than is consistent with their error bars, leading one to suspect that the errors have been underestimated. In this case, one could use the scatter to create a reasonable uncertainty on the binned average. For the current CMB data there is no clear indication of scatter inconsistent with the errors so this is unnecessary.

If one wishes to perform a model-dependent analysis of the data, the simplest reasonable approach is to compare the observations with the broad-band power estimates that should have been produced given a particular theory (the theory's C are not constant so the window functions must be used for this). Combining full raw datasets is superior but computationally intensive (see Bond et al. 1998a). A first-order correction for the non-gaussianity of the likelihood function of the band-powers has been calculated by Bond et al. (1998b) and is available at http://www.cita.utoronto.ca/~knox/radical.html.

² This figure and our compilation of CMB anisotropy observations are available at http://mamacass.ucsd.edu/people/gawiser/cmb.html; CMB observations have also been compiled by Smoot & Scott (1998) and at http://space.mit.edu/home/tegmark/cmb/experiments.html and
http://www.cita.utoronto.ca/~knox/radical.html Back.