


The second part of these lectures is an introduction to several methods to detect non-baryonic dark matter. We will use the lightest neutralino as our guinea pig, because of the variety of techniques that can be employed to detect it, but the discussion is more general and can be applied to a generic WIMP. Thus in this second part we assume that non-baryonic dark matter is made of WIMPs (in particular, neutralinos), and we examine several observational ways to test our assumption.
Neutralino dark matter searches are traditionally divided into two main categories: (1) direct detection of Galactic dark matter in laboratory experiments, and (2) indirect detection of neutralino annihilation products. For the sake of exposition, indirect searches are further subdivided into: (2a) searches for high-energy neutrinos from the center of the Sun or of the Earth; (2b) searches for anomalous cosmic rays and gamma-rays from galactic halos, especially our own; and (2c) searches for neutrinos, gamma-rays, and radio waves from the Galactic Center. We now examine each of them in turn.
The idea here is that neutralino dark matter is to be found not only in the halo of our galaxy and in our solar system, but also here on Earth and in the room we are in. Thus if we could set up a detector that records the passage of dark matter neutralinos, we could hope of detecting neutralino dark matter.
A process that can be used for this purpose is the elastic scattering of neutralinos off nuclei. Inelastic scattering could also be used in principle, as could scattering off electrons, but the rate of these processes are expected to be (much) smaller.
Dozens of experiments worldwide, too numerous to be all listed here, are using or plan to use elastic scattering to search for neutralino dark matter, or WIMP dark matter in general. The small expected detection rate, and the necessity of suppressing any ionizing radiation passing through the detector, are reasons to shelter these experiments from cosmic rays, e.g. by placing them in mines or underground laboratories.
Generally, with the notable exception of directional detectors described below, only the energy deposited in the detector during the elastic scattering can be measured. This energy is of the order of a few keV, for typical neutralino masses and speeds in the galactic halo. The kinetic energy of the recoiling nucleus is converted partly into scintillation light or ionization energy (giving an electric current) and partly into thermal energy (heating up the detector).
In cryogenic detectors, a simultaneous measurement of both ionization and thermal energy allows the discrimination of nuclear recoils from electrons produced in radioactive decays or otherwise. This discrimination, however, cannot tell if the nuclear recoil was caused by a WIMP or an ambient neutron. The detector, most often a germanium or silicon crystal, needs to be cooled at liquid helium temperature so that its low heat capacity converts a small deposited energy into a large temperature increase. Only relatively small crystals can be currently used in these cryogenic detectors, with relatively low detection rates.
Detection rates can be increased by using bigger detectors operated at room temperature, at the expense of giving up a measurement of the thermal energy and loosing discrimination power against electrons. The biggest dark matter detector is currently of this type. It is a sodium iodide crystal (a scintillator) under the Gran Sasso mountain in Italy, and it belongs to the Italian-Chinese collaboration DAMA (short for DArk MAtter). Interestingly, the loss of discrimination power and the gain in target mass almost compensate each other, and the sensitivity of cryogenic and scintillation detectors is not very different.
Few years ago, the DAMA collaboration reported a possible detection of
WIMP dark matter
(Belli, 1997;
Bernabei et
al., 2000,
1998,
2003,
1999).
Their most recent data
(Bernabei et
al., 2003)
span 7 years and show a
6.3 modulation in their
total counting rate (signal+background) with a period of 1 year and an
amplitude of ~ 0.02 events/day per kg of detector and keV of visible
recoil energy
(Figure 9). This kind of yearly modulation in a
WIMP signal was predicted by
Drukier,
Freese, & Spergel (1986) and
Freese, Frieman,
& Gould (1988)
on the basis that the velocity of the Earth around the Sun adds
vectorially to the velocity of the Sun in the Galaxy to produce a yearly
modulation in the average speed of the WIMPs relative to the Earth (the
WIMPs are assumed on average at rest in the Galaxy). For an observer on
the Earth, the WIMP `wind' arrives at a higher speed when the Earth and
the Sun move in the same direction and at a lower speed when they move
in opposite directions. (The two velocities are actually misaligned by ~
60°; see Figure 10.) The WIMP flux, and
the WIMP detection rate, both proportional to the relative speed of the
Earth and the WIMPs, are similarly modulated.
modulation in their
total counting rate (signal+background) with a period of 1 year and an
amplitude of ~ 0.02 events/day per kg of detector and keV of visible
recoil energy
(Figure 9). This kind of yearly modulation in a
WIMP signal was predicted by
Drukier,
Freese, & Spergel (1986) and
Freese, Frieman,
& Gould (1988)
on the basis that the velocity of the Earth around the Sun adds
vectorially to the velocity of the Sun in the Galaxy to produce a yearly
modulation in the average speed of the WIMPs relative to the Earth (the
WIMPs are assumed on average at rest in the Galaxy). For an observer on
the Earth, the WIMP `wind' arrives at a higher speed when the Earth and
the Sun move in the same direction and at a lower speed when they move
in opposite directions. (The two velocities are actually misaligned by ~
60°; see Figure 10.) The WIMP flux, and
the WIMP detection rate, both proportional to the relative speed of the
Earth and the WIMPs, are similarly modulated.
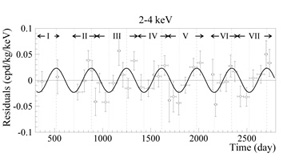 |
Figure 9. Annual modulation of the total
counting rate (background plus possible dark matter signal) in seven
years of data with the DAMA-NaI detector. A constant counting rate has
been subtracted to give the `residuals.' The significance of the
modulation is
6 |
While the presence of a yearly modulation in the DAMA data seems now to be established, its interpretation as due to WIMPs is controversial. Firstly, it is not hard to imagine that the background itself can undergo seasonal variations with a period of a year. The DAMA collaboration has examined many possible sources of background variation, including a yearly modulation of the cosmic ray intensity underground due to winter-summer temperature changes in the upper atmosphere. They claim to have found no annual variation in the background level that would produce an amplitude as big as the observed one. Secondly, the EDELWEISS cryogenic detector has sensitivity comparable to DAMA's but has not recorded any nuclear recoil event (Benoit et al., 2002). And the CDMS-I cryogenic detector, also of comparable sensitivity, has detected nuclear recoil events attributed to ambient neutrons in the shallow site where the detector was running (Akerib et al., 2003). Comparison of these experimental results is however not as straightforward as it may seem, because the relationship between detection rates in cryogenic and scintillation detectors depends, among other things, on the kind of WIMP-nucleus interaction and on details of the WIMP velocity distribution in the halo, which are both poorly known.
This dependence is apparent in the expression for the expected counting rate per recoil energy bin and unit detector mass dR / dE. We have
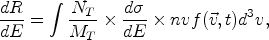 |
(40) |
where NT and MT are the number of
target nuclei and the detector mass, respectively,
d / dE is
the WIMP-nucleus differential cross section, and
nvf (
/ dE is
the WIMP-nucleus differential cross section, and
nvf ( ,
t) is the WIMP flux impinging on the
detector. Here n denotes the WIMP density, v the WIMP
speed, and
f (
,
t) is the WIMP flux impinging on the
detector. Here n denotes the WIMP density, v the WIMP
speed, and
f ( , t)
d3v the WIMP
velocity distribution. We write MT /
NT = M, the nuclear mass, n =
, t)
d3v the WIMP
velocity distribution. We write MT /
NT = M, the nuclear mass, n =
 / m,
and d
/ m,
and d / dE =
/ dE =
 0|
F(q)|2 / Emax, where
0|
F(q)|2 / Emax, where
 0 is the
total scattering cross section of a WIMP off a fictitious point-like
nucleus, | F(q)|2 is a nuclear form factor that
depends on the momentum transfer
q = (2ME)1/2 and is normalized as F(0) =
1, and
Emax = 2µ2 v2
/ M is the maximum recoil energy imparted by a WIMP of speed
v (µ = mM / (m + M) is the
WIMP-nucleus reduced mass). Hence
0 is the
total scattering cross section of a WIMP off a fictitious point-like
nucleus, | F(q)|2 is a nuclear form factor that
depends on the momentum transfer
q = (2ME)1/2 and is normalized as F(0) =
1, and
Emax = 2µ2 v2
/ M is the maximum recoil energy imparted by a WIMP of speed
v (µ = mM / (m + M) is the
WIMP-nucleus reduced mass). Hence
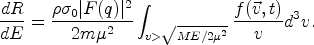 |
(41) |
Notice that one can only measure the product

 0 with this
technique. Notice also that the event rate at energy E depends on
the WIMP velocity distribution at speeds v > (ME /
2µ2)1/2. This integration limit
depends on the nuclear mass, and thus detectors with different kinds of
nuclei are sensitive to different regions of the WIMP velocity
space. Moreover, the cross section
0 with this
technique. Notice also that the event rate at energy E depends on
the WIMP velocity distribution at speeds v > (ME /
2µ2)1/2. This integration limit
depends on the nuclear mass, and thus detectors with different kinds of
nuclei are sensitive to different regions of the WIMP velocity
space. Moreover, the cross section
 0 scales
differently for spin-dependent and spin-independent WIMP-nucleus
interactions. Finally, while there is a consensus on the
spin-independent nuclear form factors, spin-dependent form factors are
sensitive to detailed modeling of the proton and neutron wave functions
inside the nucleus (see
Jungman,
Kamionkowski & Griest, 1996,
and references therein).
0 scales
differently for spin-dependent and spin-independent WIMP-nucleus
interactions. Finally, while there is a consensus on the
spin-independent nuclear form factors, spin-dependent form factors are
sensitive to detailed modeling of the proton and neutron wave functions
inside the nucleus (see
Jungman,
Kamionkowski & Griest, 1996,
and references therein).
For spin-independent interactions with a nucleus with Z protons and A - Z neutrons, one has
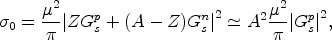 |
(42) |
where Gps and
Gns are the scalar four-fermion couplings
of the WIMP with point-like protons and neutrons, respectively (see, e.g,
Gondolo, 1996).
The last approximation holds for the case
Gps
 Gns, which is typical of a neutralino. The
spin-independent event rate, proportional to
Gns, which is typical of a neutralino. The
spin-independent event rate, proportional to
 0 /
µ2, scales with the square of the atomic number
A (if we neglect the form factor). It is this dependence on
A that allows detectors with relatively heavy nuclei to reach
down to WIMP-proton cross sections typical of weak interactions.
0 /
µ2, scales with the square of the atomic number
A (if we neglect the form factor). It is this dependence on
A that allows detectors with relatively heavy nuclei to reach
down to WIMP-proton cross sections typical of weak interactions.
For spin-dependent interactions, one has instead
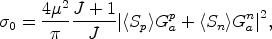 |
(43) |
where J is the nuclear spin, <Sp> and <Sn> are the expectation values of the spin of the protons and neutrons in the nucleus, respectively, and Gpa and Gna are the axial four-fermion couplings of the WIMP with point-like protons and neutrons (see Gondolo, 1996; Tovey et al., 2000). There is no increase of the spin-dependent rate with A2, and spin-dependent cross sections of the order of weak cross sections are hard to reach with current detector technology.
Given all these ambiguities in the comparison of cryogenic and scintillator results, it is the author's opinion that the important issue if WIMP dark matter has been detected is not settled yet. A bigger DAMA detector and an upgraded CDMS detector running in the low-background Soudan mine are currently taking data. EDELWEISS is also improving their sensitivity, and new experiments, like CRESST-II and ZEPLIN-IV, should start taking data shortly.
Current bounds and future reach
The sensitivity of some future experiments is shown in Figure 11, together with the current best bounds from the cryogenic detectors CDMS-I (Akerib et al., 2003) and EDELWEISS (Benoit et al., 2002), and the region where DAMA claims evidence for a WIMP signal ( Bernabei et al., 2003). As it is conventional in comparing results from different experiments, the figure shows the WIMP-proton spin-independent cross section obtained from experimental data using Eq. (42) under the assumption of a Maxwellian distribution with conventional parameters for the WIMP velocity. For an historical perspective, the figure also displays the first observational bound on WIMP dark matter obtained by Ahlen et al. (1987).
We also indicate theoretical predictions for a Dirac neutrino with
standard model couplings, and for the lightest neutralino in two
supersymmetric scenarios: minimal supergravity as in
Ellis, Ferstl,
& Olive (2000)
(shaded yellow region) and weak-scale MSSM as in Baltz & Gondolo
(2003,
2001)
(black crosses and magenta squares). Theory models assume that the
respective dark matter particles fill up the galactic halo.
Dirac neutrinos are excluded as main constituents of galactic dark
matter in the mass range 3 GeV - 3 PeV (the bounds continue linearly to
the right of the figure). These are the bounds from dark matter searches
used in
Section 2.2 (and
Figure 3) to conclude that a
yet-undetected particle species is needed to provide cold dark matter.
For the neutralino, the expected scattering cross section varies in a
wide range. Even with the most restrictive assumptions of the
Constrained Minimal Supersymmetric Standard Model (CMSSM) in
Ellis, Ferstl,
& Olive (2000),
the cross section at a given neutralino mass can change by an order of
magnitude when the other supersymmetric parameters are changed (shaded
yellow region in Figure 11). For neutralino
masses m ~ 400 GeV, the CMSSM model parameters may conspire
to make the spin-independent cross section arbitrarily small (if such is
the case, the total cross section will be dominated by spin-dependent
terms, which are however much smaller for the heavy nuclei in current
detectors). The highest CMSSM cross sections are within reach of the
upcoming experiments, although outside the current best bounds.
Other studies of supergravity models (e.g.
Feng, Matchev,
& Wilczek, 2000)
are less restrictive and result in somewhat larger cross sections.
Enlarging the parameter space beyond supergravity, as for example in
Baltz & Gondolo
(2003,
2001),
opens up more possibilities for the values of the cross section. This
happens basically for two main reasons; (i) The supergravity relation
between the masses of squark and sleptons on one side and Higgs bosons
on the other side is removed; the Higgs boson can thus be lighter, and
the spin-dependent scattering cross section, which varies essentially
with the fourth inverse power of the Higgs mass, can be larger; (ii) It
is no longer required that the electroweak symmetry breaking is achieved
radiatively, with the consequence that the gaugino and higgsino content
of the lightest neutralino can be arbitrary; the scattering cross
section is then enhanced because mixed neutralinos couple to nucleons
stronger than pure gauginos or pure higgsinos. This explains the larger
extent of the region covered by the Baltz & Gondolo
(2003,
2001)
models in Figure 11. Finally, the region in
Figure 11 marked by the magenta squares
indicates the subset of the supersymmetric models examined by
Baltz & Gondolo
(2003,
2001)
that could be able to quantitatively explain the
~ 3
~ 400 GeV, the CMSSM model parameters may conspire
to make the spin-independent cross section arbitrarily small (if such is
the case, the total cross section will be dominated by spin-dependent
terms, which are however much smaller for the heavy nuclei in current
detectors). The highest CMSSM cross sections are within reach of the
upcoming experiments, although outside the current best bounds.
Other studies of supergravity models (e.g.
Feng, Matchev,
& Wilczek, 2000)
are less restrictive and result in somewhat larger cross sections.
Enlarging the parameter space beyond supergravity, as for example in
Baltz & Gondolo
(2003,
2001),
opens up more possibilities for the values of the cross section. This
happens basically for two main reasons; (i) The supergravity relation
between the masses of squark and sleptons on one side and Higgs bosons
on the other side is removed; the Higgs boson can thus be lighter, and
the spin-dependent scattering cross section, which varies essentially
with the fourth inverse power of the Higgs mass, can be larger; (ii) It
is no longer required that the electroweak symmetry breaking is achieved
radiatively, with the consequence that the gaugino and higgsino content
of the lightest neutralino can be arbitrary; the scattering cross
section is then enhanced because mixed neutralinos couple to nucleons
stronger than pure gauginos or pure higgsinos. This explains the larger
extent of the region covered by the Baltz & Gondolo
(2003,
2001)
models in Figure 11. Finally, the region in
Figure 11 marked by the magenta squares
indicates the subset of the supersymmetric models examined by
Baltz & Gondolo
(2003,
2001)
that could be able to quantitatively explain the
~ 3 deviation between
the measured value and the Standard Model value of the magnetic moment
of the muon. 5 These models
have relatively light masses for supersymmetric partners, and give
neutralino-proton cross sections which are relatively large and within
the reach of the most ambitious future experiments.
deviation between
the measured value and the Standard Model value of the magnetic moment
of the muon. 5 These models
have relatively light masses for supersymmetric partners, and give
neutralino-proton cross sections which are relatively large and within
the reach of the most ambitious future experiments.
We conclude this section by mentioning the very intriguing possibility of WIMP detectors that are sensitive to the direction of nuclear recoils (directional detectors).
The advantages of measuring the recoil direction are multiple: a more
powerful background discrimination; the detection of the new modulation
effects, such as a daily modulation in the arrival direction of WIMPs
due to the Earth rotation around its axis; and the exciting possibility
of reconstructing the WIMP velocity distribution in the solar
neighborhood. The latter is possible because of a simple relation
between the WIMP velocity distribution
f ( , t)
and the nuclear recoil rate differential in both energy E and
recoil direction
, t)
and the nuclear recoil rate differential in both energy E and
recoil direction
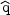 (Gondolo,
2002),
(Gondolo,
2002),
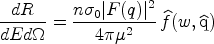 |
(44) |
where d is an
infinitesimal solid angle around the direction
is an
infinitesimal solid angle around the direction
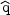 ,
w = (ME / 2µ2)1/2, and
,
w = (ME / 2µ2)1/2, and
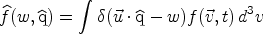 |
(45) |
is the Radon transform of the WIMP velocity distribution.
A promising development in this direction is the DRIFT detector (Snowden-Ifft, Martoff, & Burwell, 2000). This detector consists of a negative ion time projection chamber, the gas in the chamber serving both as WIMP target and as ionization medium for observing the nuclear recoil tracks. The direction of the nuclear recoil is obtained from the geometry and timing of the image of the recoil track on the chamber end-plates. A 1 m3 prototype has been successfully tested, and a 10 m3 detector is under consideration.
Directional detection is particularly powerful for detecting structure in the dark matter velocity space, as discussed in the next section on the Sagittarius stream.
Recent observations
of the stellar component of the Galactic halo show evidence of a
merger history that has not yet become well mixed, and corroborate
previous indications that
halos form hierarchically. In particular, the Sloan Digital Sky Survey
(Newberg et
al., 2003)
and the Two Micron All Sky Survey
(Majewski,
Skrutskie, Weinberg, & Ostheimer, 2003)
have traced the tidal stream
(Ibata et al.,
2001)
of the Sagittarius (Sgr) dwarf spheroidal galaxy. The
Sagittarius dwarf spheroidal galaxy, of roughly
109
M , is a
satellite of our own much larger Milky Way
Galaxy, located inside the Milky Way, ~ 12 kpc behind the Galactic
Center and ~ 12 kpc below the Galactic Plane
(Ibata et al.,
1997).
Two streams of matter are being tidally pulled away from the main body of
the Sgr galaxy and extend outward from it. These streams, known as the
leading and trailing tidal tails, are made of matter tidally pulled away
from the Sgr galaxy. It appears that the leading tail is showering
matter down upon the solar neighborhood
(Majewski,
Skrutskie, Weinberg, & Ostheimer, 2003).
The flow is in the general direction orthogonal to the Galactic plane
and has a speed of roughly 300 km/s. This speed is comparable to
that of the relative speed of the Sun and the WIMPs in the general
dark halo.
, is a
satellite of our own much larger Milky Way
Galaxy, located inside the Milky Way, ~ 12 kpc behind the Galactic
Center and ~ 12 kpc below the Galactic Plane
(Ibata et al.,
1997).
Two streams of matter are being tidally pulled away from the main body of
the Sgr galaxy and extend outward from it. These streams, known as the
leading and trailing tidal tails, are made of matter tidally pulled away
from the Sgr galaxy. It appears that the leading tail is showering
matter down upon the solar neighborhood
(Majewski,
Skrutskie, Weinberg, & Ostheimer, 2003).
The flow is in the general direction orthogonal to the Galactic plane
and has a speed of roughly 300 km/s. This speed is comparable to
that of the relative speed of the Sun and the WIMPs in the general
dark halo.
It is natural to expect that dark matter is associated with the detected tidal streams. Hence one can hope to detect the stream in direct detection experiments. The detectability depends on the density of dark matter in the stream. The mass-to-light ratio M / L in the stream is unknown, but is plausibly at least as large as that in the Sgr main body; in fact, the M / L in the stream may be significantly larger because the dark matter on the outskirts of the main body would be tidally stripped before the (more centrally located) stars. Various determinations of the M / L for the Sgr main body give values in the range 25 to 100 (see the discussion in Majewski, Skrutskie, Weinberg, & Ostheimer, 2003 and references therein). Freese, Gondolo, & Newberg (2003) and Freese, Gondolo, Newberg, & Lewis (2003) have estimated the density of dark matter in the stream, and find it to be in the range 0.3% to 23% of the local (smoothed) dark halo density. This agrees with a previous theoretical study on the tidal disruption of satellite galaxies falling into the halo of our own Milky Way by Stiff, Widrow, & Frieman (2001). These authors found that, with probability of order 1, the Sun should be situated within a stream of density ~ 4% of the local Galactic halo density.
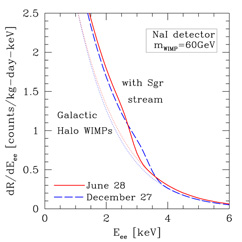
The additional flux of WIMPs from the stream shows up as a 0.3-23% increase in the rate of nuclear recoils at energies below a characteristic energy Ec, the highest energy that WIMPs in the stream can impart to a target nucleus. Hence, there is a step in the energy recoil spectrum; the count rate in the detector is enhanced at low energies, but then returns to the normal value (due to Galactic halo WIMPs) at all energies above the critical energy Ec. This feature can be observed as a sharp decrease in the count rate above a characteristic energy that depends on the mass of the target nucleus, the mass of the WIMP, and the speed of the stream relative to the detector. Figures 12(a) and (b) show how the recoil spectrum dR/dE is modified by the presence of the stream for a sodium iodide detector (like in DAMA) and a germanium detector (like for CDMS and EDELWEISS). For the sake of illustration, the plots assume a stream density equal to 20% of the local halo density.
 |
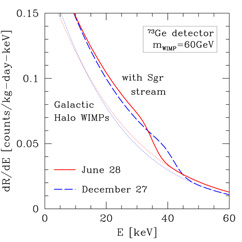 |
Figure 12. Effect of the presence of WIMPs in the Sagittarius leading tidal arm. Count rate of 60 GeV WIMPs in (a) an NaI detector such as DAMA and (b) a Ge detector such as CDMS and EDELWEISS, as a function of recoil energy. The dotted lines (towards the left) indicate the count rate due to Galactic halo WIMPs alone for an isothermal halo. The solid and dashed lines indicate the step in the count rate that arises if we include the WIMPs in the Sgr stream for vstr = 300 km/s in the direction dispersion (l, b) = (90°, -76°) with a stream velocity dispersion of 20 km/sec. The plot assumes that the Sgr stream contributes an additional 20% of the local Galactic halo density. The solid and dashed lines are for June 28 and December 27 respectively, the dates at which the annual modulation of the stream is maximized and minimized. (Figure from Freese, Gondolo, & Newberg, 2003.) |
|
Excitingly, the effect of the stream should be detectable in DAMA,
CDMS-II, and other upcoming detectors, and may already be present in the
current DAMA data. A detail calculation
(Freese,
Gondolo, & Newberg, 2003)
predicts the presence of stream WIMPs in the data with a significance of
100 for DAMA and
11
for DAMA and
11 for CDMS if the
stream density is 20% of the local halo density, and a significance of
24
for CDMS if the
stream density is 20% of the local halo density, and a significance of
24 for DAMA and
3
for DAMA and
3 for CDMS if the stream
density is 4% of the local halo density. (These significance figures are
however very sensitive to the velocity assumed for the stream,
cfr.
Freese, Gondolo,
Newberg, & Lewis, 2003.)
for CDMS if the stream
density is 4% of the local halo density. (These significance figures are
however very sensitive to the velocity assumed for the stream,
cfr.
Freese, Gondolo,
Newberg, & Lewis, 2003.)
Directional detection will be a fantastic means of recognizing the
presence of a dark stream through the Solar system. The recoil
distribution due to WIMPs in a stream is very much different from the
recoil distribution due a Maxwellian velocity distribution. The
corresponding Radon transforms that appear in Eq. (44) are: for a stream
of velocity 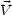 ,
,
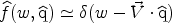 |
(46) |
which is non-zero only on the surface of a sphere in (w
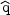 x,
w
x,
w
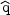 y,
w
y,
w
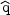 z)
space; for a Maxwellian of bulk velocity
z)
space; for a Maxwellian of bulk velocity
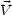 and velocity
dispersion
and velocity
dispersion  ,
,
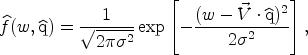 |
(47) |
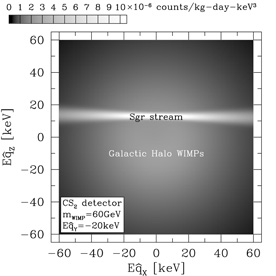
which is a smooth gaussian distribution. For our Sgr stream, consider a
next-generation DRIFT detector of 30 m3 (DRIFT-2). The
difference in the recoil direction distributions of stream and
isothermal WIMPs is apparent in Figure 13,
where we plot the differential detection rate
E-2dR / dEd
 for DRIFT-2 under
the assumption of a 20% stream density. Aa seen in the figure, a large
DRIFT detector will have the capability of clearly identifying WIMPs in
the Sgr stream.
for DRIFT-2 under
the assumption of a 20% stream density. Aa seen in the figure, a large
DRIFT detector will have the capability of clearly identifying WIMPs in
the Sgr stream.
 |
 |
Figure 13. Count rate of 60 GeV
WIMPs in a CS2 detector (DRIFT) as a
function of recoil energy E and direction of the nuclear recoil
( |
|
Besides the direct detection of galactic neutralino dark matter in the laboratory, we can search for dark matter neutralinos by looking for the products of their annihilation. We distinguish three types of searches according to the place where neutralino annihilations occur. The first is the case of neutralino annihilation in the Sun or the Earth, which gives rise to a signal in high-energy neutrinos; the second is the case of neutralino annihilation in the galactic halo, or in the halo of external galaxies, which generates gamma-rays and other cosmic rays such as positrons and antiprotons; the third is the case of neutralino annihilations around black holes, in particular around the black hole at our Galactic Center.
All these annihilation signals share the property of being proportional to the square of the neutralino density. This follows from the fact that the neutralino is a Majorana fermion, i.e. is identical to its antiparticle. Two neutralinos can annihilate to produce standard model particles. Simple stoichiometry then tells us that the annihilation rate, being proportional to the product of the densities of the initial particles, is proportional to the square of the neutralino density. In more detail, we have
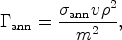 |
(48) |
where
 ann is
the neutralino annihilation rate per unit volume (i.e. the number of
neutralinos that are annihilated per unit volume and unit time),
ann is
the neutralino annihilation rate per unit volume (i.e. the number of
neutralinos that are annihilated per unit volume and unit time),
 ann is the
neutralino-neutralino annihilation cross section, v is the
relative speed of the two annihilating neutralinos,
ann is the
neutralino-neutralino annihilation cross section, v is the
relative speed of the two annihilating neutralinos,
 is the
neutralino mass density, and m is the neutralino mass. Recall
that the annihilation cross section
is the
neutralino mass density, and m is the neutralino mass. Recall
that the annihilation cross section
 ann goes as
1/v at small speeds, as required by kinematical arguments, and
thus the product
ann goes as
1/v at small speeds, as required by kinematical arguments, and
thus the product
 annv
does not vanish linearly with v (and is not small at the
relatively small speeds of neutralinos in galactic halos).
Notice also that the number of annihilations per unit volume and unit
time is given by
1/2
annv
does not vanish linearly with v (and is not small at the
relatively small speeds of neutralinos in galactic halos).
Notice also that the number of annihilations per unit volume and unit
time is given by
1/2 ann,
where the factor of
1/2 correctly converts between the number of annihilation events and the
number of neutralinos that are annihilated (2 per annihilation). It is
easy to get confused with this factor of 1/2.
ann,
where the factor of
1/2 correctly converts between the number of annihilation events and the
number of neutralinos that are annihilated (2 per annihilation). It is
easy to get confused with this factor of 1/2.
If in the annihilation rate
 ann we
insert a typical weak interaction cross section and a typical value for
the average dark matter density in the Universe, the annihilation rate
we obtain gives undetectably small signals. Indirect detection is
possible because dark matter is not distributed uniformly in
space. Galaxies and clusters of galaxies are overdensities in the dark
matter field, as is any possible substructure in galactic
halos. Furthermore, dark matter may be concentrated gravitationally
around massive objects, and may even get trapped inside planets and
stars. The neutralino annihilation rate, proportional to the square of
the neutralino density, increases substantially in these dark matter
concentrations, sometimes to the point of giving observable signals.
ann we
insert a typical weak interaction cross section and a typical value for
the average dark matter density in the Universe, the annihilation rate
we obtain gives undetectably small signals. Indirect detection is
possible because dark matter is not distributed uniformly in
space. Galaxies and clusters of galaxies are overdensities in the dark
matter field, as is any possible substructure in galactic
halos. Furthermore, dark matter may be concentrated gravitationally
around massive objects, and may even get trapped inside planets and
stars. The neutralino annihilation rate, proportional to the square of
the neutralino density, increases substantially in these dark matter
concentrations, sometimes to the point of giving observable signals.
High energy neutrinos from the core of the Sun or of the Earth
Neutralinos floating around the solar system can occasionally collide with nuclei in the Sun and in the planets (the Earth, in particular). In these collisions, they may loose enough kinetic energy to end up with a speed smaller than the escape speed, thus becoming gravitationally trapped. After some time, the trapped neutralinos will sink to the core of the celestial body in which they are captured, and will possibly reach a condition of thermal equilibrium (Figure 14).
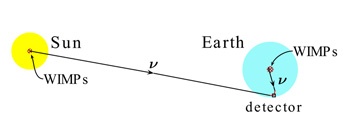 |
Figure 14. Illustration of indirect detection of WIMPs using high-energy neutrinos emitted in WIMP annihilations in the core of the Sun or of the Earth. |
Once concentrated in the center, neutralinos annihilate copiously. The annihilation rate is maximal when all captured neutralinos annihilate (a condition called equilibrium between capture and annihilation). Whether this condition is satisfied depends on the relative strength of the annihilation and scattering cross sections, and ultimately on the parameters of the particle and halo models. (See Jungman, Kamionkowski & Griest, 1996 and references therein for complete formulas.)
Of the annihilation products produced in the center of the Earth and the Sun only the neutrinos make it to the surface; all the other products are absorbed or decay within a short distance of production. All three flavors of neutrinos are produced for neutralino masses which are currently allowed. Direct production of a neutrino pair is however strongly suppressed in neutralino annihilation, due to the Majorana nature of the neutralino. Annihilation neutrinos are instead produced as secondaries in the decay chains of the primary particles produced in the neutralino-neutralino annihilation. As a consequence, the neutrino energy spectrum is a continuum, and the typical energy of neutrinos from neutralino annihilations is about a tenth of the neutralino mass. Given the current constraints, this means a neutrino energy between few GeVs and few TeVs.
Neutrinos of this energy can be detected in Cherenkov neutrino telescopes, whose principle of operation is depicted in Figure 15. A charged-current interaction in the material surrounding the detector (rock, ice, water) converts the neutrino into its corresponding charged lepton, which then radiates Cherenkov light in the detector medium (ice or water). Several neutrino telescopes are currently operational (among them the Super-Kamiokande detector in Japan and the AMANDA detector at the South Pole), and others are under construction or development (IceCube at the South Pole, ANTARES and NESTOR in the Mediterranean). Other neutrino telescopes have played a role in dark matter searches in the past, such as the IMB, the Fréjus, the MACRO, and the Baksan experiments.
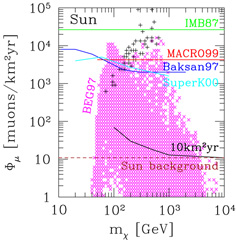
The current experimental situation for this indirect detection method is summarized in Figure 16(a) for neutrinos from WIMPs in the Sun, and Figure 16(b) for neutrinos from WIMPs in the Earth. The figures show the current best bounds from the MACRO, Baksan, Super-Kamiokande, and AMANDA experiments, as well as the first bound obtained using this technique by the IMB collaboration in 1987. Also shown is the reach of the IceCube experiment after an exposure of 10 km2 yr, and the ultimate applicability of this method for the Sun, which is set by the emission of high-energy neutrinos in cosmic ray interactions with nuclei on the surface of the Sun.
 |
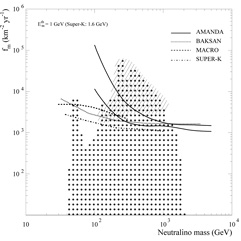 |
Figure 16. Indirect searches for neutralino dark matter using high-energy neutrinos from (left) the Sun and (right) the Earth. On the vertical axis is the flux of neutrino-induced muons that traverse the neutrino telescope, on the horizontal axis is the neutralino mass. `IMB87' is the historically first upper limit, `MACRO,' `BAKSAN,' `SuperK,' and `AMANDA' are the limits from the corresponding experiments. The regions marked by × on the left and by dots on the right are the predictions of supersymmetric models defined at the weak scale (Ahrens et al., 2002; Bergström, Edsjö, & Gondolo, 1998). The + signs on the left and the shaded region on the right indicate the regions where there are models that have been excluded by direct dark matter searches. The line labeled `10km2yr' shows the maximum reach of such an exposure in IceCube, and the line labeled `Sun background' marks the level of high-energy neutrino emission due to cosmic ray interactions on the surface of the Sun, which is the ultimate applicability limit of this method. (Figure on the left from Gondolo, 2000; figure on the right from Ahrens et al., 2002.) |
|
Expectations from theoretical models in Figure 16 (MSSM with seven weak-scale parameters) range from cases which are already excluded by this method to cases which this indirect method will be unable to explore. In comparison, direct searches have a different coverage of theoretical models. The reach of direct searches is indicated in the Figure 16 by + signs in the left panel and by the shading in the right panel (direct searches exclude only some of the theoretical models that are projected onto these regions from the higher-dimensional supersymmetric parameter space). There are models that can be explored by direct searches and not by indirect searches of high-energy neutrinos from the Sun and the Earth. And vice versa, there are theoretical models that cannot be explored by direct searches but can be explored by indirect searches of high-energy neutrinos from the Sun or the Earth. The latter aspect is illustrated in Figure 17, where models that can be reached by indirect searches for neutrinos from neutralinos in the Sun are marked by dots in the scattering cross section-mass plane, and compared with the sensitivity of several current and future direct search experiments. Several models fall beyond the reach of even the most ambitious direct dark matter searches. This shows the (everlasting) complementarity between direct and indirect neutralino searches.
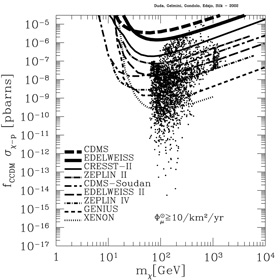 |
Figure 17. Complementarity of direct and
indirect neutralino dark matter searches. The figure shows that several
supersymmetric models that are within the (expected) reach of a big
neutrino telescope of 10 km2 yr exposure are beyond the
reach of current and future direct detection experiments. The vertical
axis is the product of the neutralino-proton spin-independent
scattering cross section
|
Gamma-rays and cosmic rays from neutralino annihilation in galactic halos
We shift now our attention to signals originating in neutralino annihilations which occur in the halo of our galaxy or in the halo of external galaxies.
The annihilation products of importance are those that are either rarely
produced in astrophysical environments or otherwise have a peculiar
characteristic that make them easily recognizable. In the first
category are rare cosmic rays such as positrons, antiprotons, and
antideuterons. In the second category are gamma-rays, whose spectrum is
expected to contain a gamma-ray line at an energy corresponding to the
neutralino mass (besides a gamma-ray continuum; see
Figure 18). The gamma-ray line is produced
directly in the primary neutralino annihilation into

 or
Z
or
Z . Positrons, antiprotons, deuterons, and the gamma
continuum are generated in the particle cascades that follow the decay
of the primary annihilation products. Their spectra are therefore
broad, with a typical energy which is only a fraction of the neutralino
mass, and a shape whose details depend on which annihilation channels
are dominant. Two neutralinos can in fact annihilate into a variety of
primary products, depending on their masses and compositions: fermion
pairs f
. Positrons, antiprotons, deuterons, and the gamma
continuum are generated in the particle cascades that follow the decay
of the primary annihilation products. Their spectra are therefore
broad, with a typical energy which is only a fraction of the neutralino
mass, and a shape whose details depend on which annihilation channels
are dominant. Two neutralinos can in fact annihilate into a variety of
primary products, depending on their masses and compositions: fermion
pairs f ,
Higgs boson pairs HiHj, gauge boson
pairs W + W -, ZZ, etc.
,
Higgs boson pairs HiHj, gauge boson
pairs W + W -, ZZ, etc.
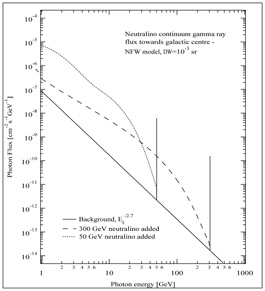 |
Figure 18. Two examples of gamma-ray spectrum from neutralino annihilation in the galactic halo. The numerical values refer to a specific model for the dark halo of our galaxy and for observations in the direction of the galactic center, but the spectral characteristics are general. Neutralino annihilations produce a gamma-ray line at an energy corresponding to the mass of the neutralino, and a gamma-ray continuum generated in the particle cascades following the primary annihilation. The figure illustrates that the shape of the continuum spectrum depends on the neutralino mass, but notice that it also depends on the neutralino composition. (Figure from Bergström, Ullio, & Buckley, 1998.) |
Detection of the gamma-ray line would be a smoking-gun for neutralino dark matter, since no other astrophysical process is known to produce gamma-ray lines in the 10 GeV - 10 TeV energy range. Good energy resolution is crucial to detect the neutralino gamma-ray line. The simulation in Figure 19 shows that the upcoming GLAST detector should have an adequate energy resolution.
For these signals, the dependence of the annihilation rate on the square of the density, see Eq. (48), has dramatic consequences. The predicted signals may change by several orders of magnitude when the model for the dark matter density is changed, even without violating observational bounds on the latter. Truly, these observational limits are not very stringent, given the understandable difficulty of measuring the dark matter density. Anyhow the problem is currently there, and can be divided roughly into two questions: (1) what is the radial dependence of the average dark matter density in a galaxy, especially in our own? (2) how much substructure, i.e. clumps and streams, is there in galactic dark halos?
Dependence on the density profile
Historically, the density profile of galactic dark halos has been given in terms of empirical density profiles whose density is constant in a central region and decreases as r-2 at large radii. The latter is the main ingredient in obtaining a flat rotation curve in the outer regions, which is a primary evidence for dark matter in galaxies. Central among these functions is the cored isothermal profile
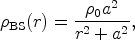 |
(49) |
where a is called the core radius (Bahcall & Soneira, 1980). This parametrization is so simple and so much used that it is sometimes called the `canonical' density profile. Another interesting empirical parametrization is the density profile of Persic, Salucci, & Stel (1996),
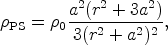 |
(50) |
which provides good fits to rotation curves of hundreds of spiral galaxies (which are not as flat as one might think!).
Numerical simulations of structure formation in the Universe have discovered that pure cold dark matter halos do not follow the previous empirical density profiles but instead have a universal shape whose parameters depend on the mass (or age) of the system. Navarro, Frenk, & White (1996) have found this universal profile to have the form
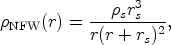 |
(51) |
where the parameter rs is the radius at which the radial dependence of the density changes from r-1 to r-3. The empirical dependence r-2 is then seen as an approximation in the transition region. Moore et al. (1998) suggest instead that the universal profile may be steeper at the center,
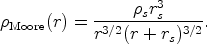 |
(52) |
Which of these two profiles better represents the results of numerical
simulations is a question that must be answered by higher resolution
simulations (which seem to be pointing to an inner slope
 that
depends on the mass of the system).
that
depends on the mass of the system).
The four profiles mentioned above are plotted in
Figure 20 for a galaxy
that could be our own, with total mass
Mvir = 2 × 1012
M and
virial radius rvir = 428 kpc.
and
virial radius rvir = 428 kpc.
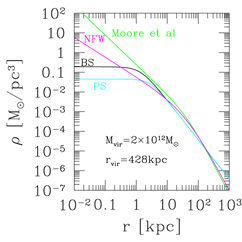 |
Figure 20. Dark matter density profiles for a galaxy resembling our own. Models `BS' (Bahcall & Soneira, 1980) and `PS' (Persic, Salucci, & Stel, 1996) are empirical parametrizations which possess a central region with constant density (core). Models `NFW' (Navarro, Frenk, & White, 1996) and `Moore et al' (Moore et al., 1998) are derived from numerical simulations of structure formation in the Universe, and in them the density in the central region increases as a power law of radius (cusp). All four models are normalized to the same total mass and virial radius. |
The essential difference between the empirical and the numerical
profiles, for what concerns neutralino signals, is their behavior at
small radii. The empirical profiles have a central region with constant
density, called a core, while the numerical profiles have a density
that increases toward the center as a power law, called a cusp. Since
the neutralino annihilation signals scale as the square of the density,
any power law
r- with
with
 > 0 is
bound to give a higher signal from the central region, for a given total
mass. Moreover, if
> 0 is
bound to give a higher signal from the central region, for a given total
mass. Moreover, if

 3/2, the annihilation rate
in the central region formally diverges, because
3/2, the annihilation rate
in the central region formally diverges, because

 2
r2 dr
2
r2 dr

 r-2
r-2 +2 dr.
+2 dr.
It is therefore crucial for our purpose to know which class of profiles, with a core or with a cusp, better resembles reality. Unfortunately, constraining a given dark matter profile using the kinematics of the central region is a hard problem, because the dynamics of the central regions is usually dominated by the visible matter, and when it is not, like in low surface brightness (LSB) spiral galaxies, the central parts are so small that the angular resolution of the observations is a major concern. Discrepant data and an apparent lack of universality in LSB profiles has generated endless controversies in the astrophysical community. At any rate, it must not be forgotten that the profiles mentioned above obtained in numerical simulations include cold dark matter only, and astrophysical processes connected for instance with the gas and the formation of stars may well modify the density profile of dark matter (theoretical work in this direction is not lacking).
In the face of this situation, when making predictions for annihilation signals from neutralino dark matter in the halo, it is prudent for the moment to consider both possibilities, core and cusp.
The considerable differences in indirect neutralino signals between a cored and a cuspy density profile are illustrated in Figure 21 for a gamma-ray signal from neutralino annihilation from the direction of the Galactic Center (without the spike contribution discussed in the next Section). There is a factor of 500 difference between assuming an NFW profile or a cored isothermal profile in the theoretical calculation of the gamma-ray flux in the seven-parameter MSSM model in Bergström, Ullio, & Buckley (1998). Superposed on the plot are the sensitivities to gamma-ray point sources of various gamma-ray telescopes, both current and upcoming (as of 2000). The comparison with the theoretical expectations in the figure is not direct, however, because the neutralino emission may not be point like in some of the telescopes. The sensitivity curves are thus only meant to provide an approximate comparison.
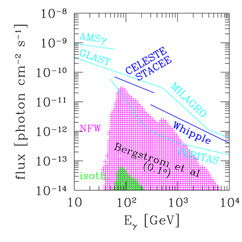 |
Figure 21. Expected gamma-ray flux in the
gamma-ray line from neutralino
annihilation in our galactic halo, coming from the direction of the
Galactic Center (without the spike discussed in next Section). The
photon energy E |
It must be mentioned here that EGRET has detected gamma-ray emission
from the direction of the Galactic Center
(Mayer-Hasselwander et al., 1998).
However, in a reanalysis of the EGRET data by
Hooper &
Dingus (2002),
the EGRET signal seems to originate from a source which is displaced
with respect to the Galactic Center.
Hooper &
Dingus (2002)
use their reanalysis to place constraints on the gamma-ray flux from
neutralino annihilations, coming to an upper limit on the gamma-ray flux
above 1 GeV which is about a factor of 2 higher than the theoretical
predictions for neutralino masses
m ~ 50 GeV, assuming an NFW profile. See
Hooper &
Dingus (2002)
for details.
~ 50 GeV, assuming an NFW profile. See
Hooper &
Dingus (2002)
for details.
The same numerical simulations that predict a cuspy dark halo profile also predict the existence of numerous dark clumps in galactic halos. These clumps are a natural outcome of the hierarchal formation of structure in the Universe. Small structures form first, and larger structures, like galaxies, grow by attracting and swallowing smaller structures. This process continues to the present day. Clumps that fall into a galaxy are pulled apart by tidal interactions: the material pulled out forms tidal streams that crisscross the galactic halo. The central parts of some of the clumps may survive for a long time, and become a galactic satellite.
The overall picture of hierarchical structure formation has found confirmation in a variety of context, from observations of galaxy clusters and of merging galaxies to the halo substructure detected in our own galaxy (see the discussion on the Sagittarius stream in Section 3.1 above, for example). A numerical discrepancy should however be mentioned. A counting of visible satellites of our own galaxy gives a number of luminous satellites that is much smaller than the expected number of dark satellites. A resolution to this discrepancy may be that only a small fraction of dark satellites becomes luminous. It is not clear why this should happen, but on the other hand we do not fully understand how galaxies become luminous in the first place. Thus for what concerns signals from neutralino annihilation, it makes sense to examine the effect of adding substructure, i.e. clumps and streams, to galactic dark halos.
Substructure in the halo tends to increase the annihilation signals
because of the dependence of the annihilation rate on the square of the
dark matter density (see Eq. (48)). The enhancement factor is linearly
proportional to the density enhancement


 ' /
' /
 . To understand
why the dependence is linear instead of quadratic in
. To understand
why the dependence is linear instead of quadratic in
 , consider a box of
volume V containing a total mass M. The density in the box
is
, consider a box of
volume V containing a total mass M. The density in the box
is  = M
/ V and the annihilation rate integrated over the whole box is
= M
/ V and the annihilation rate integrated over the whole box is
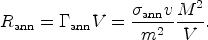 |
(53) |
Now let all the mass be concentrated equally into N small boxes,
each of volume V', so that each box contains a mass M' =
M / N and thus has a density
 ' = M' /
V'. The density enhancement is then
' = M' /
V'. The density enhancement is then
 = V /
NV'. The annihilation rate from the whole box is now given by a
sum over the N small boxes as
= V /
NV'. The annihilation rate from the whole box is now given by a
sum over the N small boxes as
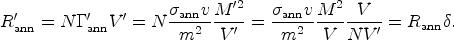 |
(54) |
One power of the density
 in
in
 ann is
compensated by a decrease in the volume where annihilations occur. Hence
the signal enhancement is linear in the density increase.
ann is
compensated by a decrease in the volume where annihilations occur. Hence
the signal enhancement is linear in the density increase.
An interesting consequence of the annihilation signal enhancement has
been explored by
Bergström,
Edsjö, & Ullio (2001) and
Ullio,
Bergström, Edsjö, & Lacey (2002).
These authors have found that the density enhancements produced during
the formation of the large scale structure in the Universe may lead to a
substantial increase in the isotropic gamma-ray background from
neutralino annihilations in the early Universe. Moreover, they found
that this increase in the gamma-ray signal is not very sensitive to
details of the galactic density profile. Expected gamma-ray spectra may
in some models be close to the measured gamma-ray background, as
illustrated in Figure 22. The gamma-ray spectra
include both a continuum
part and gamma-ray lines (two for each neutralino case: one for




 , the other
for
, the other
for 

 Z
Z  ).
The gamma-ray lines are asymmetrically broadened because photons emitted
at earlier times have a larger redshift. The gamma-ray background due to
neutralino annihilations should be searched for at high galactic
latitudes, where the galactic emission is expected to be
minimal. Detection of the line features depicted in
Figure 22 would not
require an energy resolution much better than the present one.
).
The gamma-ray lines are asymmetrically broadened because photons emitted
at earlier times have a larger redshift. The gamma-ray background due to
neutralino annihilations should be searched for at high galactic
latitudes, where the galactic emission is expected to be
minimal. Detection of the line features depicted in
Figure 22 would not
require an energy resolution much better than the present one.
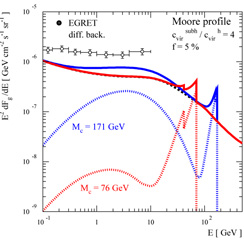 |
Figure 22. Expected isotropic gamma-ray background from neutralino annihilations in the early Universe. Dotted lines are the signal from neutralino annihilations; solid lines are the sum of the neutralino signal and a gamma-ray background of astrophysical origin. Two neutralino models are shown, together with the current EGRET measurements of the isotropic extragalactic background. The assumptions used for the dark matter profile are indicated. (Figure from Ullio, Bergström, Edsjö, & Lacey, 2002.) |
Another exciting application of a signal enhancement due to clumps in the galactic halo is the boost of the positron signal from neutralino annihilation up to the level of the excess of cosmic ray positrons observed by the HEAT collaboration. The HEAT collaboration flew two different detectors on balloons, and claims to have detected a ratio of positron to electron fluxes above ~ 7 GeV that is higher than the flux expected in current state-of-the-art models of cosmic ray production and propagation in the galaxy. These models aim at explaining all correlated signals in gamma-rays, radio waves, protons, electrons, positrons, heavy nuclei, etc. that are produced by cosmic rays in our galaxy.
One possible explanation is that the positron excess is due to the
positrons generated in neutralino annihilation in the galactic halo. If
the neutralinos are produced thermally in the early universe, which is
the most common assumption, the annihilation cross section
 ann is forced
to be small by the requirement that the neutralino relic density is
large enough for neutralinos to be the dark matter. Using the average
value of the local dark matter density, of the order of 0.3
GeV/cm2, then leads to a positron signal which is more than
an order of magnitude smaller than the excess measured by
HEAT. Increasing the annihilation cross section
ann is forced
to be small by the requirement that the neutralino relic density is
large enough for neutralinos to be the dark matter. Using the average
value of the local dark matter density, of the order of 0.3
GeV/cm2, then leads to a positron signal which is more than
an order of magnitude smaller than the excess measured by
HEAT. Increasing the annihilation cross section
 ann does not
make the signal higher, because the density
ann does not
make the signal higher, because the density
 decreases
inversely with
decreases
inversely with
 ann, and
hence the annihilation signal, being proportional to
ann, and
hence the annihilation signal, being proportional to
 ann
ann
 2,
decreases.
Kane, Wang, &
Wells (2002)
suggested that the neutralinos may not have been produced thermally in
the early Universe, and were thus able to decouple the annihilation rate
in the halo from the constraint coming out of the relic density
requirement. Alternatively,
Baltz, Edsjö,
Freese, & Gondolo (2002)
have suggested that substructure in the galactic halo may provide the
necessary boost factor to the positron signal.
2,
decreases.
Kane, Wang, &
Wells (2002)
suggested that the neutralinos may not have been produced thermally in
the early Universe, and were thus able to decouple the annihilation rate
in the halo from the constraint coming out of the relic density
requirement. Alternatively,
Baltz, Edsjö,
Freese, & Gondolo (2002)
have suggested that substructure in the galactic halo may provide the
necessary boost factor to the positron signal.
Enhancing the positron signal through clumps also enhances other
annihilation signals, such as antiprotons and gamma-rays.
Baltz, Edsjö,
Freese, & Gondolo (2002)
have performed a detailed analysis of these enhancements, and have
concluded that it is possible to explain the HEAT positron excess with
boost factors as small as 30, but typically higher, without obtaining
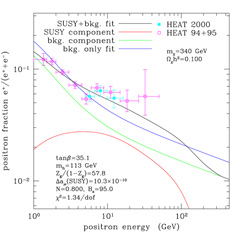
too many antiprotons or gamma-rays. Figure 23
shows two examples of
neutralino models that provide a good fit to the positron excess. On the
left, the neutralino has mass
m = 340 GeV and is an almost pure gaugino (gaugino
fraction Zg = 0.98); the boost factor is 95 and other
parameters are listed in the figure. On the right, the neutralino is
mixed (gaugino fraction
Zg = 0.70) with a mass of 238 GeV; the boost factor is
116.7. The
= 340 GeV and is an almost pure gaugino (gaugino
fraction Zg = 0.98); the boost factor is 95 and other
parameters are listed in the figure. On the right, the neutralino is
mixed (gaugino fraction
Zg = 0.70) with a mass of 238 GeV; the boost factor is
116.7. The  2 per
degree of freedom is quite good for both fits, 1.34 and 1.38
respectively.
2 per
degree of freedom is quite good for both fits, 1.34 and 1.38
respectively.
 |
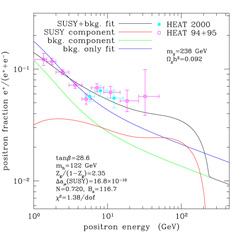 |
Figure 23. Two examples of neutralino models that provide a good fit to the excess of cosmic ray positrons observed by the HEAT collaboration. The two sets of data points (open and filled squares) are derived from two different instruments flown in 1994-95 and 2000. The lines represent: (i) the best expectation we have from models of cosmic ray propagation in the galaxy (`bkg. only fit'), which underestimate the data points above ~7 GeV; (ii) the effect of adding positrons from neutralino annihilations (lines `SUSY component', `SUSY+bkg. fit', and `bkg. component', the latter being the resulting background component when the data are fitted to the sum of background and neutralino contributions). (Figures from Baltz, Edsjö, Freese, & Gondolo, 2002). |
|
The ultimate test of the explanation of the positron excess by means of neutralino clumps will be the detection of a signal in gamma-rays. Gamma-ray production would in fact be enhanced by the same mechanism that would enhance positron production. Baltz, Edsjö, Freese, & Gondolo (2002) have found that almost all neutralino models that can explain the positron excess are within the sensitivity reach of upcoming gamma-ray telescopes (see Figure 24). The realistic possibility of confirming (or disproving) the neutralino origin of the positron excess is fascinating.
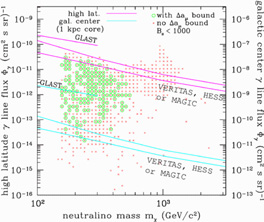 |
Figure 24. Sensitivity of upcoming gamma-ray telescopes to neutralino models that can explain the HEAT positron excess with neutralino clumps in the galactic halo. Model points are indicated by crosses; circles denote those models that in addition can also account for the measured deviation in the muon magnetic moment. The upper set of sensitivity curves corresponds to the high latitude gamma-ray line flux (scale on the left); the lower set of curves to the direction toward the galactic center (scale on the right; no steep spike around the central black hole is assumed). (Figure from Baltz, Edsjö, Freese, & Gondolo, 2002.) |
Signals from neutralino annihilation at the Galactic Center
The last indirect neutralino signals we consider are neutrinos, gamma-rays and radio waves from a possible dark matter concentration around the black hole at the Galactic Center.
Evidence for the presence of a black hole at the center of our galaxy comes from studies of the motion of stars in orbit around the center. The speeds of these stars decrease from the center as the inverse square root of the radius, which is the primary indication for the existence of a point mass at the center. The mass of the central object is measured to be ~ 4 × 106 solar masses, which are contained within a sphere of less than ~ 0.05 pc (Eckart & Genzel, 1997; Ghez, Klein, Morris, & Becklin, 1998; Ghez et al., 2003). No stellar or gas system can be so dense, indicating that the central object is most probably a black hole. The position of the black hole happens to coincide with the position of a strong radio source called Sagittarius A*, which is thus identified with the central black hole.
The radio emission from Sgr A* is easily explained by thermal emission of hot matter falling into the black hole. However, contrary to many of the similar black holes observed at the center of external galaxies, our galactic black hole does not emit intensely in the X-ray band, and it is controversial if it emits gamma-rays. Models for such `quiet' black holes do exist, however, such as those involving advection-dominated accretion flows (ADAFs).
Further evidence for a black hole at the center of the Milky Way comes from the 2001 observation of a X-ray and infrared flares from the Galactic Center (Genzel et al., 2003b; Porquet et al., 2003; Baganoff et al., 2001). The flare time scale and intensity can nicely be explained if the flare is produced near a black hole (see, e.g., Aschenbach, Grosso, Porquet, & Predehl, 2004).
Dark matter may be driven near the black hole gravitationally, and may form a dense concentration around it (Gondolo & Silk, 1999). We will call this concentration a spike, so as to distinguish it from the dark matter cusps of Section 3.2.2. The formation of a spike is gravitational phenomenon similar to but less efficient than accretion of matter, in that the latter involves dissipation of energy and angular momentum and can thus produce concentrations which are smaller and denser.
How strong is the dark matter concentration around Sgr A*, or around a generic black hole? This is still a matter of investigation. The simplest case is that of adiabatic compression, and was analyzed by Gondolo & Silk (1999).
Adiabatic compression of an initial dark matter distribution produces
two kinds of spikes. If the initial distribution before the black hole
forms is thermal, the spike is shallow, with density profile

 r-3/2. If the initial phase-space distribution is a
power-law in energy, the spike is steep, i.e.
r-3/2. If the initial phase-space distribution is a
power-law in energy, the spike is steep, i.e.

 r-
r- with
with
 >
2. The physical reason for the higher concentration in the second case
is the presence of many dark matter orbits with low speed, which are
more easily driven into bound orbits when the black hole forms.
>
2. The physical reason for the higher concentration in the second case
is the presence of many dark matter orbits with low speed, which are
more easily driven into bound orbits when the black hole forms.
These two kinds of spike are illustrated in
Figure 25 for the same four
halo models discussed in Section 3.2.2. Models with
a core, like those by
Bahcall &
Soneira (1980)
and
Persic, Salucci,
& Stel (1996),
give rise to a shallow spike around the central black hole, while models
with a cusp, like those of
Navarro, Frenk,
& White (1996)
and
Moore et
al. (1998),
produce steep spikes. In the very inner regions, the density may become
so high that neutralino-neutralino annihilations may have had the time
to deplete the number of neutralinos and an `annihilation plateau' is
formed. The typical radius of a spike around a black hole is determined
by the radius of influence of the black hole,
rinfl ~ GM /
 v2, which is the radius at which the
gravitational potential energy becomes comparable to the typical kinetic
energy in the dark matter gas (M is the black hole mass and
v2, which is the radius at which the
gravitational potential energy becomes comparable to the typical kinetic
energy in the dark matter gas (M is the black hole mass and
 v is the gas
velocity dispersion). For the black hole at the Galactic Center,
rinfl ~ 1 pc.
v is the gas
velocity dispersion). For the black hole at the Galactic Center,
rinfl ~ 1 pc.
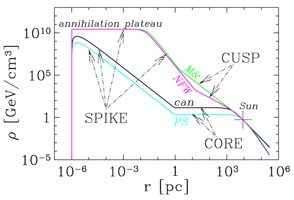 |
Figure 25. Density profiles of spikes that form adiabatically around the black hole at the center of our Galaxy. The position of the Sun is indicated by a cross. Four models for the halo profile are shown: two with cores (`PS' by Persic, Salucci, & Stel (1996) and `can' by Bahcall & Soneira (1980)) and two with cusps (`NFW' by Navarro, Frenk, & White (1996) and `M&' by Moore et al. (1998)). The spikes form within the radius of influence of the black hole, rinfl ~ 1 pc. In the `annihilation plateau' neutralino annihilations have been so rapid as to deplete the number of neutralinos. (Figure from Buckley et al., 2001.) |
Neutralino annihilation is enhanced in the spike, because of the dependence of the annihilation rate on square of the density. The Galactic Center then becomes a source of neutrinos, gamma-rays, radio waves, etc. from neutralino annihilation (Figure 26). The intensity of the emission depends on the steepness of the spike. If the spike is shallow, neutralino annihilation is generally undetectable. On the contrary, a steep spike at the Galactic Center produces interesting signals.
For example, if, disregarding Hooper & Dingus's reanalysis mentioned above, we attribute the EGRET gamma-ray emission from the Galactic Center to neutralino annihilation in a spike born out of an NFW profile, we obtain a high-energy neutrino flux that is either excluded or mostly detectable in a km3 neutrino telescope (Figure 27). The flux of neutrino-induced muons above 25 GeV would be detectable over the atmospheric neutrino background for neutralino masses between ~ 100 GeV and ~ 2 TeV, while heavier neutralinos would already be excluded from the current limit on the neutrino emission from the Galactic Center (Habig et al., 2001).
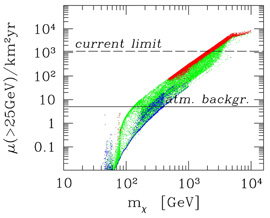 |
Figure 27. Predicted neutrino signal from neutralino dark matter annihilation in a steep adiabatic spike at the Galactic Center expressed as number of neutrino-induced muons per km2-yr in a neutrino telescope. The spike corresponds to an NFW profile. Each dot in the figure corresponds to a point in a seven-parameter weak-scale MSSM, and is normalized so that the gamma-ray flux from the spike coincides with the gamma-ray signal from the Galactic Center observed by EGRET. Models with heavy neutralinos are excluded by the current limit on the neutrino emission from the Galactic Center; models with neutralinos as light as ~ 100 GeV could be detected above the atmospheric neutrino background. (Figure from Gondolo, 2002b.) |
As a second and more dramatic example (Gondolo, 2000b), electrons and positrons from neutralino annihilation would emit synchrotron radiation as they spiral in the magnetic field that plausibly exists around the central black hole. While this synchrotron radiation is innocuous for a shallow adiabatic spike, it may exceed the observed radio emission by several orders of magnitude if the spike is steep. The radio synchrotron emission at 408 MHz is shown in Figure 28 for an adiabatic spike born out of an NFW profile, under two assumptions for the radial dependence of the magnetic field (a constant field of 1 mG and a field in equipartition with the infalling gas). In both cases, all dark matter neutralinos in the seven-parameter MSSM models considered are strongly excluded.
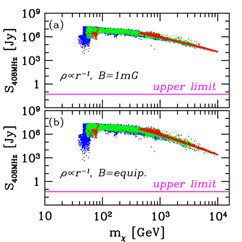 |
Figure 28. Synchrotron emission at 408 MHz expected from neutralino dark matter annihilation in a steep adiabatic spike at the Galactic Center. The spike corresponds to an NFW profile, and the synchrotron radiation is emitted by electrons and positrons produced in neutralino annihilation. Upper panel: constant magnetic field; lower panel: equipartition magnetic field. All dark matter neutralinos in the seven-parameter weak-scale MSSM considered are excluded by several orders of magnitude. (Figure from Gondolo, 2000b.) |
The examples above have assumed that the spike formed adiabatically and maintained its shape till the present time. This may not be the case.
For example, if the central black hole formed through the merging of two black holes of similar mass, Merritt, Milosavljevic, Verde, & Jimenez (2002) have shown that the spike would become shallow at the end of the merging, because dark matter particles would be kicked out of the black hole region via a gravitational sling-shot effect. The final shallow spike would not give dramatic signals from neutralino annihilation at the Galactic Center. In a realistic scenario of this type, the two merging black holes of similar mass would be accompanied by their host galaxies whose mass would also be similar. The merging would then constitute what is known as a major merging. A major merging is capable of destroying the Galactic disk, and so must not have occurred after the disk formed about 1010 years ago. Thus, for this scenario to work, black holes of millions of solar masses should already have been in place at very early times. Is this possible? While hard to explain theoretically, supermassive black holes have indeed been observed in very distant quasars, at redshift z > 6, so the scenario may be plausible.
In these considerations, it must be kept in mind that there is a stellar
spike around the black hole at the Galactic Center. The steepness of
this stellar spike is however not very well know. With large
uncertainties,
Genzel et
al. (2003)
estimate the slope of the stellar spike to be
 stars ~ 1.3-1.4. This means that the current
stellar spike is probably shallow. We may think that the stellar spike
is our best proxy for the dark matter spike. If so, also the dark matter
spike would also be shallow, and thus inconsequential for neutralino
signals. However, the dark matter and stellar spikes follow very
different evolution histories, because contrary to the dark matter,
binary collisions of stars and coalescence of two stars into one at
collisions effectively relax the stellar system to a shallower spike.
stars ~ 1.3-1.4. This means that the current
stellar spike is probably shallow. We may think that the stellar spike
is our best proxy for the dark matter spike. If so, also the dark matter
spike would also be shallow, and thus inconsequential for neutralino
signals. However, the dark matter and stellar spikes follow very
different evolution histories, because contrary to the dark matter,
binary collisions of stars and coalescence of two stars into one at
collisions effectively relax the stellar system to a shallower spike.
The final word has not yet been said regarding the distribution of dark matter at the Galactic Center, or around black holes and other compact objects in general. This is one of the exciting points of contact between the study of dark matter and the study of the formation and evolution of galactic nuclei.
5 The size of the deviation has been hard to determine conclusively because of the difficulty of the non-perturbative QCD calculations involved, in particular their dependence on the data used as input. There is also a story on sign errors in some of the theoretical calculations.... Back.