4. THEORETICAL FRAMEWORK

4.1. The Relativistic Fireball Model

As discussed in the introduction, the ultimate energy source of GRB is convincingly associated with a catastrophic energy release in stellar mass objects. For long bursts, this is almost certainly associated with the late stages of the evolution of a massive star, namely the collapse of its core [514, 346], which at least in some cases is associated with a detectable supernova. For short bursts, it has been long assumed [343, 105] that they were associated with compact binary mergers (NS-NS or NS-BH), a view which is gaining observational support [40, 130], although the issue cannot be considered settled yet. In both cases, the central compact object is likely to be a black hole of several solar masses (although it might, temporarily, be a fast rotating high-mass neutron star, which eventually must collapse to black hole). In any case, the gravitational energy liberated in the collapse or merger involves of order a few solar masses, which is converted into free energy on timescales of milliseconds inside a volume of the order of tens of kilometers cubed. This prompt energy is then augmented by a comparable amount of energy release in a similar or slightly larger volume over a longer timescale of seconds to hundreds of seconds, by the continued infall or accretion of gas onto the central object, either from the central parts of the massive progenitor star or from the debris of the disrupted compact stars which was temporarily held up by its rotation.

The principal result of the sudden release of this large gravitational energy (of order a solar rest mass) in this compact volume is the conversion of a fraction of that energy into neutrinos, initially in thermal equilibrium, and gravitational waves (which are not in thermal equilibrium), while a significantly smaller fraction (10^-2 - 10^-3) goes into a high temperature fireball (kT MeV) consisting of e^±, -rays and baryons. The fireball is transparent to the gravitational waves, and beyond several interaction lengths, also to the neutrinos. This leads to the prompt emission (on timescales of a few seconds) of roughly comparable energy amounts (several × 10⁵³ ergs) of thermal _{e e} with typical energies 10-30 MeV, and of gravitational waves mainly near 10² - 10³ Hz. These two, by far most dominant, energy forms are so far undetected, and are discussed further in Section 9. A smaller fraction of the liberated energy, or order 10⁵⁰ - 10⁵² ergs remains trapped in a e^±, -ray and baryon fireball, which can also contain a comparable (or in some scenarios a larger) amount of magnetic field energy. This amount of energy is observed, mainly as non-thermal gamma-rays. While smaller than the predicted thermal neutrino and gravitational wave fluence, this is nonetheless a formidable electromagnetic energy output, much more intense than any other explosive event in the universe. While the total energy is comparable to the electromagnetic and kinetic energy of supernovae, the difference is that in supernovae the energy is doled out over months, mainly at optical wavelengths, while in GRB most of the electromagnetic energy is spilled out in a matter of seconds, and mainly at -ray wavelengths.

The leading model for the electromagnetic radiation observed from GRBs is based on the relativistic fireball created in the core collapse or merger. The photon luminosity inferred from the energies and timescales discussed and from the observations is many orders of magnitude larger than the Eddington luminosity L_e = 4 GM m_p c / _T = 1.25× 10³⁸(M / M) erg s^-1, above which radiation pressure exceeds self-gravity, so the fireball will expand. The first (thermal) fireball models were assumed to reach relativistic expansion velocities [64, 343, 167, 446]. However, the ultimate expansion velocity depends on the baryon load of the fireball [344]. If the fireball energy involved all the baryons in the core (solar masses) the expansion would be sub-relativistic. However, near the black hole the density is reduced due to accretion and centrifugal forces, it is likely that baryons are much depleted in the region where the fireball forms, with a tendency to form high entropy (high energy/mass ratio) radiation bubbles. Dynamically dominant magnetic fields would also tend to involve fewer baryons. A phenomenological argument shows that the expansion must, indeed, be highly relativistic. This is based on the fact that most of the GRB spectral energy is observed above 0.5 MeV, so that the mean free path for the e^± process in an isotropic plasma (an assumption appropriate for a sub-relativistically expanding fireball) would be very short. This leads to a contradiction, since many bursts show spectra extending above 1 GeV, so the flow must be able to avoid degrading these via photon-photon interactions to energies below the threshold m_e c² = 0.511 MeV [191]. To avoid this, it seems inescapable that the flow must be expanding with a very high Lorentz factor , since then the relative angle at which the photons collide is less than ^-1 and the threshold for the pair production is then diminished. This condition is

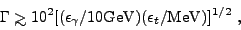(1)

in order for photons to escape annihilation against target photons of energy _t ~ 1 Mev [297, 191]. I.e., a relativistically expanding fireball is expected, with bulk Lorentz factors = 100 ₂ 1.

4.2. Reference frames and timescales in relativistic flows

The emitting gas is moving relativistically with velocity = v / c = (1 - 1 / ²)^1/2 relative to a laboratory frame K_* which may be taken to be the origin of the explosion or stellar frame (which, aside from a cosmological Doppler or redshift factor is the same as the Earth frame K of an observer). The lengths, times, thermodynamic and radiation quantities of the gas are best evaluated in the gas rest frame (the comoving frame) K', and are obtained in the stellar/lab frame through Lorentz transformations. Thus, a proper length dr' in the comoving frame has a stellar/lab frame length dr_* = dr' / (if both ends r_{* 1} and r_{* 2} of the length dr_* = r_{* 1} - r_{* 2} in K_* are measured at the same time so dt_* = 0 in K_*; i.e. the usual Fitz-Gerald contraction). Similarly, a proper time interval dt' in the comoving frame has a duration dt_* = dt' in K_* (provided the times t_{* 1} and t_{* 2} of dt_* = t_{* 1} - t_{* 2} in K_* are measured at same positions x_{* 1} and x_{* 2} in K_* so dx_* = 0; the usual time dilation effect). The time needed in the stellar/lab frame K_* for the gas to move from x_{* 1} to x_{* 2} is the usual dt_* = t_{* 1} - t_{* 2} = dr_* / c dr_*/c.

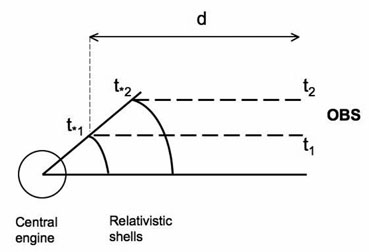Figure 4. Illustration of the emission from spherical relativistic shells in the source frame and the relativistic time delay leading to the relation between source frame time and observer time.

When it comes to observations at Earth of radiation emitted from the relativistically moving gas, even though the Earth frame K is essentially the same as the K_* stellar/lab frame, in addition to the above Lorentz transformations one has to consider also the classical light travel time delay (Doppler) effect, e.g. [424]. In the observer frame K one can use the same spatial coordinates r r_* and dr dr_* as in K_*, but the actual time of arrival of signals as measured by an observer, which is for brevity denoted just t, differs from t_* by the above Doppler effect, t t_*. Since this observed time t is the actual observable, it is customary to describe GRB problems in terms of t (remembering it is t_*) and r (which is = r_*). Considering a gas which expands radially in a direction at an angle cos = µ respect to the observer line of sight, if a first photon is emitted when the gas is at the radius r_{* 1} = r₁ (which is at a distance d from the observer) at t_{* 1}, this photon arrives at the observer at an observer time t₁ = t_{* 1} - d / c. A second photon emitted from a radius r_{* 2} = r₂ at time t_{* 2} will arrive at an observer time t₂ = t_{* 2} + (d / c - µ dt_*), where dt_* = t_{* 1} - t_{* 2}. This is illustrated in the source frame in Figure 4. For an observer close to the line of sight the observed time difference between the arrival of the two photons is

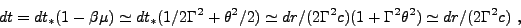(2)

where we assumed >> 1 for an approaching gas (µ = cos > 0) along a radial direction well inside the light cone << ^-1.

While both dt and dt_* are in the same reference frame, K = K_*, the difference is that dt_* is the time difference between emission of the two photons, and dt is the time difference between reception of the two photons. The general relation between the observer frame and comoving frame quantities is given through the Doppler factor ,

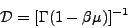(3)

where ~ 2 for an approaching gas with >> 1, µ 1 and < ^-1 (blueshift), or ~ 1/2 for a receding gas with µ -1 (redshift). Thus, the relation between the comoving frame dt' and the observer frame time dt is

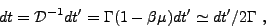(4)

where an approaching gas is assumed with < ^-1 (while dt_* = dt' ). This is illustrated in terms of observer-frame quantities in Figure 5. Note that in all the above transformations we have neglected cosmological effects, which would result in multiplying any reception or observer-frame times by an additional factor (1 + z) for signals emanating from a source at redshift z.

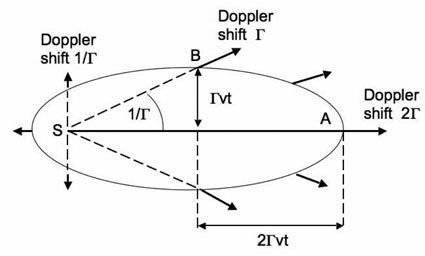Figure 5. For a distant observer (located to the right) viewing a shell which expands spherically from S with = [1 - (v / c)2]1/2 >> 1, the locus of the points from which radiation reaches it at a later time t appears as a spheroid (equal arrival time surface). Most of the radiation arrives from the forward (right) hemisphere, which is strongly Doppler boosted inside the light cone 1 / (after [402]). The apparent transverse radius of the ellipsoid is r ct, and its semi-major axis is r|| ct, where t is observer time.

The relation between the source frame and observer frame frequency, solid angle, specific intensity, temperature, volume, specific emissivity, specific absorption coefficient and radial width are obtained in terms of the Doppler factor using relativistic invariants [424], = ', d = ^-2 d', I() = ³ I'_'('), T() = T'('), dV = dV', j() = ² j'_'('), µ() = ^-1µ'_'('), r = ^-1 r'. Here µ = n (in cm^-1, where n is density and is absorption cross section), and both µ and the optical depth are invariants.

4.3. Relativistic dynamics

From general considerations, an outflow arising from an initial energy E₀ imparted to a mass M₀ << E₀ / c² within a radius r₀ will lead to an expansion, which due to the initial high optical depth can be considered adiabatic. The pressure will be dominated by radiation, so the adiabatic index is _a = 4/3, and the comoving temperature T' (or comoving random Lorentz factor per particle ') evolves with comoving volume V' as T V'^{1- _a}. With a comoving volume V' r³ (equation [8]) this means T' ' r^-1. By conservation of energy, this decrease in internal energy per particle is balanced by an increase in its expansion-related energy, i.e. the bulk kinetic energy per particle or bulk Lorentz factor , so that = constant, so that r. This expansion occurs at the expense of the comoving frame internal energy. Since the bulk Lorentz factor per particle cannot increase beyond the initial value of random internal energy per particle, ₀ = = E₀ / M₀ c², the bulk Lorentz factor only grows until it reaches _max ~ = E_o / M_o c², which is achieved at a radius r / r₀ ~ . Beyond this radius the flow begins to coast, with ~ ~ constant [343, 167, 446, 345],

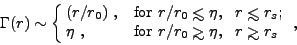(5)

which defines a saturation radius r_s ~ r₀ beyond which the Lorentz factor has saturated. Another way to understand the initial acceleration [300] is that initially, at r = r₀, the gas particles have a bulk Lorentz factor ~ 1 and have an isotropical distribution of velocities with random Lorentz factors ~ = E₀ / M₀ c². As the particles expand outward, when they have reached a radius r their velocity vectors will confined inside an angle (r / r₀)^-1 of the radial direction. A transformation to a comoving frame moving radially with a bulk Lorentz factor (r) ~ r / r₀ is needed for the velocity distribution to be isotropic in the comoving frame, as it should be.

As particles initially contained inside r₀ move outwards with velocity vectors which are increasingly radial, they form a radially expanding shell whose lab-frame width is initially r ~ r_o ~ r_o. The radial velocity spread is (c - v) / c = 1 - ~ ^-2, which causes a gradual spread of the lab-frame radial width r / r ~ v / v ~ ^-2. For typical values of r₀ ~ 10⁶-10⁷ cm and 10³ this is negligible until well beyond the saturation radius, and a noticeable departure from the approximately constant width r ~ r_o starts to become appreciable only for radii in excess of a spreading radius r where r ~ r v / c ~ r ^-2 r_o. The laboratory frame width is therefore [300]

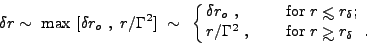(6)

where the spreading radius r ~ r₀ ² is a factor larger than the saturation radius r_s ~ r₀ .

The comoving radial width r' is related to the lab width r through r' = r ~ r . Hence

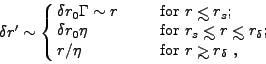(7)

Since the dimensions transverse to the motion are invariant, the comoving volume is V' r² r', which behaves as [300]

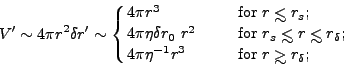(8)

and the comoving particle density n' V'^-1. For an adiabatic expansion (valid for the high initial optical depths) and a relativistic gas polytropic index 4/3 (valid as long as the pressure is dominated by radiation), one has

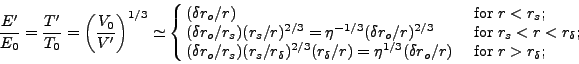(9)

where E', T', ', V' are comoving internal energy, temperature, density and volume.

The above equations refer to the release of an energy E₀ and mass M₀ corresponding to = E₀ / M₀ c², originating inside a region of dimension r₀ ~ r₀. This mass and energy leaves that original region in a lab-frame (or observer frame) light-crossing time t₀ ~ r₀ / c. For typical core collapse or compact merger stellar scenarios, the energy release volume is of the order of several Schwarzschild radii of the ensuing black hole (BH), few times 2GM_BH / c² with M_BH 2 M, say r₀ ~ 10⁷ m₁ cm, where m₁ = M_BH /10 M, with a light-crossing timescale t₀ ~ r₀ / c ~ 3 × 10^-4 m₁ s. This is of the order of the dynamical (Kepler) timescale near the last stable circular orbit in a temporary accretion disk feeding the newly formed black hole (or near the light cylinder of an initial fast-rotating magnetar or neutron star, before it collapses to a black hole).

4.4. Optical Depth and Photosphere

As shown by [343, 167, 446] a relativistically expanding fireball initially has e^± pairs in equilibrium which dominate the scattering optical depth, but the pairs fall out of equilibrium and recombine below a comoving temperature T' ~ 17 keV, and thereafter only a residual freeze-out density of pairs remains, which for not too large (in practice 10⁵ i.e. baryon loads not too small) is much less than the density of "baryonic" electrons associated with the protons, n_e = n_p. For a typical burst conditions the initial black-body temperature T'₀ at r₀ ~ 10⁷ cm is a few MeV, and pair recombination occurs at radii below the saturation radius. The scattering optical depth of a minishell (and of the whole outflow) is still large at this radius, due to the baryonic electrons. For a minishell of initial width r₀ the optical depth varies as [300]

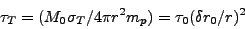(10)

where ₀ = (E_{0 T} / 4 r₀² m_p c² ), for r_o r / ² or r r. Assuming a burst with total energy E₀ = 10⁵² E₅₂ and total duration t_grb divided into minishells of duration t₀ = 3 × 10^-4 s, each of energy 10^47.5 E_47.5 erg, these becomes optically thin at

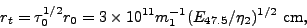(11)

where henceforth the notation Q_x (where x is a number) indicates the quantity Q in units of 10^x times its c.g.s. units.

For bursts of some substantial duration, e.g. an outflow duration t_grb = 10 s as above, at any instant different parts of the flow have different densities, and are above or below the saturation radius, so a continuous outflow picture is more appropriate [344]. In this "wind" regime one defines the dimensionless entropy as = L / c², and instead of integral conservation laws one uses the relativistic fluid differential equations. The Lorentz factor again grows linearly and saturates at the same radius r_s = r₀ (equation [5]), where r₀ = r₀ is the minimum variability radius, and the adiabatic behavior of equation (9) is the same for the temperature, etc. The particle density follows from the mass conservation equation,

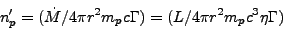(12)

and the optical depth is _T(r) = _r n'_{e T} [(1 - ) / (1 + )]^1/2 dr' ~ n'_{e T} (r / 2) which yields for the global photosphere [344]

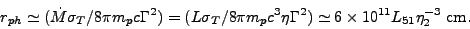(13)

The comoving temperature of the flow behaves as T' r^-1, r^-2/3 and the observer-frame temperature T = T' is T ~ T₀, T ~ T₀(r / r_s)^-2/3 for r < r_s, r > r_s (equations [9]).

The radiation escaping from a radius r (e.g. the photospheric radius r_ph) which is released at the same stellar frame time t_* would arrive at the observer only from within angles inside the light cone, < ^-1. The observer-frame time delay between light coming from central line of sight and the edges of the light cone (the so-called angular time [167]) is

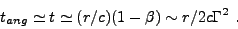(14)

This is because the `edge' of the light cone corresponds to an angle of 1 / from the line of sight, and therefore ct_ang ~ r(1 - cos) ~ r(1 - ) ~ r/2², since at = 1 / , cos . This time is the same as the observer-frame time of equation (2). Note that if the outflow duration t_grb is shorter than t_ang of equation (14), the latter is the observed duration of the photospheric radiation (due to the angular time delay). Otherwise, for t_grb > t_ang, the photospheric radiation is expected for a lab-frame duration t_grb.

4.5. Thermal vs. Dissipative Fireballs and Shocks

The spectrum of the photosphere would be expected to be a black-body [343, 167, 446], at most modified by comptonization at the higher energy part of the spectrum. However, the observed -ray spectrum observed is generally a broken power law, i.e., highly non-thermal. In addition, a greater problem is that the expansion would lead to a conversion of internal energy into kinetic energy of expansion, so even after the fireball becomes optically thin, it would be highly inefficient, most of the energy being in the kinetic energy of the associated protons, rather than in photons. For a photosphere occurring at r < r_s, which requires high values of , the radiative luminosity in the observer frame is undiminished, since E'_rad r^-1 but r so E_rad ~ constant, or L_ph r^{2 2} T'⁴ constant, since T' r^-1. However for the more moderate values of the photosphere occurs above the saturation radius, and whereas the kinetic energy of the baryons is constant E_kin ~ E₀ ~ constant the radiation energy drops as E_rad (r / r_s)^-2/3, or L_ph ~ L₀ (r_ph / r_s)^-2/3 [301, 310].

A natural way to achieve a non-thermal spectrum in an energetically efficient manner is by having the kinetic energy of the flow re-converted into random energy via shocks, after the flow has become optically thin [403, 301, 300, 217, 404, 438]. Such shocks will be collisionless, i.e. mediated by chaotic electric and magnetic fields rather than by binary particle interactions, as known from interplanetary experiments and as inferred in supernova remnants and in active galactic nuclei (AGN) jets . As in these well studied sources, these shocks can be expected to accelerate particles via the Fermi process to ultra-relativistic energies [43, 2, 108, 265, 450], and the relativistic electron component can produce non-thermal radiation via the synchrotron and inverse Compton (IC) processes. A shock is essentially unavoidable as the fireball runs into the external medium, producing a blast wave. The external medium may be the interstellar medium (ISM), or the pre-ejected stellar wind from the progenitor before the collapse. For an outflow of total energy E₀ and terminal coasting bulk Lorentz factor ₀ = expanding in an external medium of average particle density n_ext, the external shock becomes important at a deceleration radius r_dec for which E₀ = (4 / 3) r_dec³ n₀ m_p c^{2 2} [403],

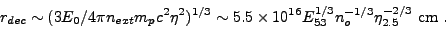(15)

At this radius the initial bulk Lorentz factor has decreased to approximately half its original value, as the fireball ejecta is decelerated by the swept-up external matter. The amount of external matter swept at this time is a fraction ^-1 of the ejecta mass M₀, M_ext ~ M₀ / (in contrast to the sub-relativistic supernova expansion, where deceleration occurs when this fraction is ~ 1).

The light travel time difference between a photon originating from r = 0 and a photon originating from matter which has moved to a radius r with a Lorentz factor is t ~ (r / c)(1 - ) ~ r / 2c ² [402], and the emission from a photosphere or from a shock emission region at radius r moving at constant is also received from within the causal light cone angle ^-1 on an observer angular timescale t ~ r / 2c ² [403, 301]. For an explosion which is impulsive (i.e. essentially instantaneous as far as observed relativistic time delays) a similarity solution of the relativistic flow equations shows that the bulk of the ejected matter at a radius r is mainly concentrated inside a region of width r ~ r / 2² [44, 45]. The time delay between radiation along the central line of sight originating from the back and front edges of this shell also arrive with a similar time delay t ~ r / 2c . Thus, the timescale over which the deceleration is observed to occur is generally

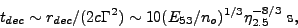(16)

and this is the observer timescale over which the external shock radiation is detected. This is provided that the explosion can be taken to be impulsive, which can be defined as the outflow having a source-frame (and observer frame) duration t_grb < t_dec (see however Section 4.6). Variability on timescales shorter than t_dec may occur on the cooling timescale or on the dynamic timescale for inhomogeneities in the external medium, but is not ideal for reproducing highly variable profiles [439], and may therefore be applicable to the class of long, smooth bursts. However, it can reproduce bursts with several peaks [355], and if the external medium is extremely lumpy (n_o / n_o 10⁵ - 10⁶) it might also describe spiky GRB light curves [96].

Before the ejecta runs into the external medium, "internal shocks" can also occur as faster portions of the ejecta overtake slower ones, leading to pp collisions and ⁰ decay gamma-rays [387] and to fast time-varying MeV gamma-rays [404]. The latter can be interpreted as the main burst itself. If the outflow is described by an energy outflow rate L_o and a mass loss rate _o = dM_o / dt starting at a lower radius r_l, maintained over a time T, then the dimensionless entropy is = L_o / _o c², and the behavior is similar to that in the impulsive case, r and comoving temperature T' r^-1, followed by saturation _max ~ at the radius r / r_o ~ [344]. For variations of the output energy or mass loss of order unity, the ejected shells of different Lorentz factors ~ are initially separated by c t_v (where t_v T are the typical variations in the energy at r_l), and they catch up with each other at an internal shock (or dissipation) radius

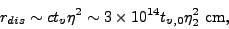(17)

The time variability should reflect the variability of the central engine, which might be expected e.g. from accretion disk intermittency, flares, etc. [331]. The radiation from the disk or flares, however, cannot be observed directly, since it occurs well below the scattering photosphere of the outflow and the variability of the photons below it is washed out [404]. The comoving Thomson optical depth is _T = n'_{e T} r / , and above the saturation radius r_s = r_o where = , the radius of the photosphere (_T = 1), is given from equation (13) as

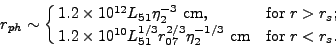(18)

The location of this baryonic photosphere defines a critical dimensionless entropy _* = 562 (L₅₁ / r₀₇)^1/4 above (below) which the photosphere occurs below (above) the saturation radius [310]. In order for internal shocks to occur above the wind photosphere and above the saturation radius (so that most of the energy does not come out in the photospheric quasi-thermal radiation component) one needs to have 3.3 × 10¹ (L₅₁ r_0,7 / t_v,0)^1/5 5.62 × 10² (L₅₁ / r_0,7)^1/4. The radial variation of the bulk Lorentz factor and the location of the various characteristic radii discussed above is shown in Figure 6.

Figure 6. Jet Lorentz factor schematic behavior and examples of nominal locations of the saturation radius rs, photospheric radius rph, internal shock (or magnetic dissipation) radius ris and external shock res. The photosphere produces thermal -rays, the internal shock/dissipation region produces the non-thermal -rays, the external shock region produces the afterglow.

Such internal shock models have the advantage [404] that they allow an arbitrarily complicated light curve, the shortest variation timescale t_v,min 10^-4 s being limited only by the dynamic timescale at r₀ ~ c t_v,min ~ 10⁷ r_0,7 cm, where the energy input may be expected to vary chaotically, while the total duration is t_grb >> t_v. Such internal shocks have been shown explicitly to reproduce (and be required by) some of the more complicated light curves [439, 227, 358] (see however [96, 425]). The gamma-ray emission of GRB from internal shocks radiating via a synchrotron and/or inverse Compton mechanism reproduces the general features of the gamma-ray observations [138, 451]. There remain, however, questions concerning the low energy (20-50 keV) spectral slopes for some bursts (see Section 4.7). Alternatively, the main -ray bursts could be (at least in part) due to the early part of the external shock [403, 96]. Issues arise with the radiation efficiency, which for internal shocks, is estimated to be moderate in the bolometric sense (5 - 20%), higher values ( 30-50%) being obtained if the shells have widely differing Lorentz factors [451, 31, 232], although in this case one might expect large variations in the spectral peak energy E_peak between spikes in the same burst, which is problematic. The total efficiency is substantially affected by inverse Compton losses [362, 374]. The efficiency for emitting in the BATSE range is typically low ~ 1 - 5%, both when the MeV break is due to synchrotron [245, 451, 185] and when it is due to inverse Compton [354].

4.6. Duration, reverse shocks, thin and thick shells

In the following discussion we assume for simplicity a uniform external medium. For a baryonic outflow such as we have been considering, the timescale t₀ ~ r₀ / c ~ ms represents a minimum variability timescale in the energy-mass outflow. (Note, however, if the gamma-ray emission arises from local dissipation events, such as e.g. magnetic reconnection in a Poynting flux dominated outflow, the minimum timescales could be smaller than the timescales of the central source variations). On the other hand, the total duration t_grb of the outflow, during which the central engine keeps pouring out energy and matter, is likely to be substantially longer than the minimum variability timescale t₀. The temporary accretion disk must have an outer radius larger than r₀, and a total accretion (or jet energization) time t_grb >> t₀ (or the magnetar has a spin-down time t_grb >> t₀). Thus, in general the total lab-frame width of the outflow ejecta will be ct_grb, which may be viewed as composed of many radial minishells whose individual widths are r ~ c t₀ or larger. While the saturation radius is still r_s ~ r₀ where r₀ ~ r₀ corresponds to the shortest variability time (and the smallest minishells coast after this r_s), the entirety of the ejecta reaches coasting speed only after its leading edge has moved to a larger radius r_s' ~ , and the ejecta as whole starts to spread at a larger radius r ~ ² (even though individual minishells of initial width r << start to spread individually at the smaller radius r ~ r ²).

In general, whatever the duration t_grb of the outflow, one expects the external shock to have both a forward shock (blast wave) component propagating into the external medium, and a reverse shock propagating back into the ejecta [301]. The forward shock and the reverse shock start forming as soon as the outflow starts, although their radiation is initially weak and increases progressively. The forward shock is highly relativistic, ~ from the very beginning, but the reverse shock starts initially as a sub-relativistic sound wave (relative to the contact discontinuity or shock frame) and becomes progressively stronger as more external matter is swept up. (This describes the more frequently encountered "thin shell" case, see below; the reverse shock becomes stronger with time only if the external density profile is shallower than r^-2, whereas the reverse shock strength is constant for an r^-2 profile at r < r).

For an impulsive regime outflow, where t_grb < t_dec, i.e. when the outflow time is shorter than the time-delayed duration of the external shock when it starts to decelerate, equation [16], this deceleration time can be taken to be the observable duration of the peak emission from the external shock. Thereafter the expansion goes into a self-similar expansion with r^-3/2 [44, 403]. In this case, t_dec is also the observer time at which the reverse shock finishes crossing the ejecta, and at that time the reverse shock Lorentz factor 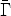_r relative to the contact discontinuity frame has become marginally relativistic, 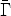_r ~ 1, while relative to the external gas or the observer, the reverse shocked gas is still moving at almost the same speed as the forward shocked gas [301, 304]. One consequence of this is that while the forward shocked protons have highly relativistic random Lorentz factors, those in the reverse shock are marginally relativistic, and consequently the electrons in the forward shock are much more relativistic than those in the reverse shock, leading to a much softer (optical) spectrum of the reverse shocks [302, 305] (see Section 5.2)

However, when the outflow time t_grb exceeds the deceleration time t_dec of equation (16), the eternal shock dynamics is different [438]. In this case there is an initial intermediate regime r^-1/2 (obtained, for a constant external density and a constant kinetic luminosity L at t < t_grb from momentum balance in the shock frame, L / (r^{2 2 2}), and the transition to a self-similar expansion r^-3/2 [44, 433] occurs at the observer time t_grb, instead of at t_dec. Thus, the observer time for the transition to the self-similar expansion is

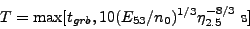(19)

This defines a critical initial Lorentz factor ₀ ~ of the burst by setting T = t_grb in place of t_dec in equation (16),

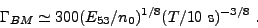(20)

For < _BM, T = t_dec we have the usual "thin shell" case, where deceleration and transition to the self-similar expansion occurs at the usual r_dec, t_dec, and at this time the reverse shock has crossed the ejecta and is marginally relativistic. For > _BM we have a "thick shell" case, where deceleration and transition to the self-similar regime occurs at T = t_grb and r_BM ~ 2cT _BM², when ~ _BM. In this > _BM case, the reverse shock becomes relativistic, and by the time it has crossed the ejecta (at time T = t_grb) the reverse shock Lorentz factor in the contact discontinuity frame is 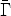_r ~ / 2_BM >> 1, and the forward shock Lorentz factor at this time is _BM.

4.7. Spectrum of the Prompt GRB Emission

The prompt emission observed from classical GRB (as opposed to XRFs or SGRs) has most of its energy concentrated in the gamma-ray energy range 0.1-2 MeV. The generic phenomenological photon spectrum is a broken power law [19] with a break energy in the above range, and power law extensions down into the X-ray, and up into the 100 MeV to GeV ranges (although a substantial fraction of GRB have soft X-ray excesses above this, and some are classified as X-ray rich (XRR) [381], a classification intermediate between XRF and GRB). For classical GRB the photon energy flux F_e E^- has typical indices below and above the typical observed break energy E_br ~ 0.2 MeV of ₁ ~ 0 and ₂ ~ 1 [19]. (Pre-BATSE analyses sometimes approximated this as a bremsstrahlung-like spectrum with an exponential cutoff at E_br, but BATSE showed that generally the extension above the break is a power law). A synchrotron interpretation is thus natural, as has been argued e.g. since the earliest external shock synchrotron models were formulated.

The simplest synchrotron shock model starts from the conditions behind the relativistic forward shock or blast wave [403, 301]. The post-shock particle and internal energy density follow from the relativistic strong shock transition relations [44],

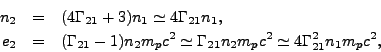(21)

where it is assumed that the upstream material is cold. Here n is number density and e is internal energy density, both measured in the comoving frames of the fluids, ₂₁ is the relative Lorentz factor between the fluids 2 (shocked, downstream) and 1 (unshocked, upstream), and the Lorentz factor of the shock front itself is _sh = 2^1/2 ₂₁, valid for ₂₁ >> 1. For internal shocks the jump conditions can be taken approximately the same, but replacing ₂₁ by a lower relative Lorentz factor _r ~ 1.

The typical proton crossing a strong shock front with a relative bulk Lorentz factor ₂₁ acquires (in the comoving frame) an internal energy characterized by a random (comoving) Lorentz factor _p,m ~ [301]. The comoving magnetic field behind the shock can build up due to turbulent dynamo effects behind the shocks [301, 302] (as also inferred in supernova remnant shocks). More recently, the Weibel instability has been studied in this context [291, 335, 294, 452]. While the efficiency of this process remains under debate, one can parametrize the resulting magnetic field as having an energy density behind the shock which is a fraction _b of the equipartition value relative to the proton random energy density behind the shock, B' ~ [32 _b n_ex ('_p - 1)m_p c²]^1/2 , where the post-shock proton comoving internal energy is ('_p - 1) m_p c² ~ 1 (or ~ ) for internal (external) shocks [301, 404]. Scattering of electrons (and protons) by magnetic irregularities upstream and downstream can lead to a Fermi acceleration process resulting in a relativistic power law distribution of energies N() ^-p with p 2. It should be stressed that although the essential features of this process are thought to be largely correct, and it is widely used for explaining supernova remnant, AGN and other non-thermal source radiation spectra, the details are only sketchily understood, [43, 2, 108, 265, 221, 450]. (Possible difficulties with the simplest version of Fermi acceleration and alternative possibilities were discussed, e.g. in [23, 192, 410]). The starting minimum (comoving) Lorentz factor of the thermal electrons injected into the acceleration process, _e,m would in principle be the same as for the protons, , (they experience the same velocity difference), hence both before and after acceleration they would have ~ (m_e / m_p) less energy than the protons. However, the shocks being collisionless, i.e. mediated by chaotic electric and magnetic fields, can redistribute the proton energy between the electrons and protons, up to some fraction _e of the thermal energy equipartition value with the protons, so _e,m ~ _e (m_p / m_e) [302, 304]. If only a fraction _e 1 of all the shocked thermal electrons is able to achieve this _e initial equipartition value to be injected into the acceleration process, then the initial minimum electron random comoving Lorentz factor is _m ~ (_e / _e)(m_p / m_e) [60], where henceforth we ignore the subscript e in _e,m. More accurately, integrating over the power law distribution, one has _m = g(p) (m_p / m_e) (_e / _e) ~ 310 [g(p) / (1/6)] (_e / _e) , where g(p) = (p - 2) / (p - 1). The observer frame synchrotron spectral peak is

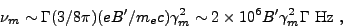(22)

and the optically thin synchrotron spectrum is [424]

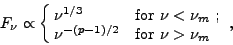(23)

assuming that the radiative losses are small (adiabatic regime). For the forward external shock at deceleration, typical values are, e.g. B' ~ 30 (_B,-1 n_ex)^1/2 _2.5 G, ~ ~ 3 × 10², _m ~ 10⁵ (_e,-1 / _e,-1) _2.5 and _m ~ 2 × 10²⁰ (_e,-1 / _e,-1)² (_B,-1 n_ex)^1/2 _2.5⁴ Hz, while for internal shocks typical values are, e.g. B' ~ 3 × 10⁵ (_B,-1 n'₁₃)^1/2 _rel,0 G, _rel ~ 1_rel,0, _m ~ 3 × 10³ (_e,-1 / _e,-1) _rel,0 and _m ~ 2 × 10¹⁹ (_e,-1 / _e,-1)² (_B,-1 n'13)^1/2 _r,0³ _2.5 Hz. For the prompt emission, the high energy slope ₂ = (p - 1)/2 is close to the mean high energy slope of the Band fit, while the low energy slope can easily approach ₁ ~ 0 considering observations from, e.g., a range of B' values (a similar explanation as for the flattening of the low energy synchrotron slope in flat spectrum radio-quasars). The basic synchrotron spectrum is modified at low energies by synchrotron self-absorption [302, 304, 217, 171], where it makes the spectrum steeper (F ~ ² for an absorption frequency _a < _m). It is also modified at high energies, due to inverse Compton effects [302, 304, 404, 98, 436, 523], extending into the GeV range.

The synchrotron interpretation of the GRB radiation is the most straightforward. However, a number of effects can modify the simple synchrotron spectrum. One is that the cooling could be rapid, i.e. when the comoving synchrotron cooling time t'_sy = 9m_e³ c⁵ / 4e⁴ B'² _e) ~ 7 × 10⁸ / B'² _e s is less than the comoving dynamic time t'_dyn ~ r / 2c , the electrons cool down to _c = 6 m_e c / _T B'² t'_dyn and the spectrum above _c ~ (3/8)(eB' / m_e c) _c² is F ^-1/2 [440, 164]. Also, the distribution of observed low energy spectral indices ₁ (where F ^₁ below the spectral peak) has a mean value ₁ ~ 0, but for a fraction of bursts this slope reaches positive values ₁ > 1/3 which are incompatible with a simple synchrotron interpretation [381]. Possible explanations include synchrotron self-absorption in the X-ray [172] or in the optical range up-scattered to X-rays [354], low-pitch angle scattering or jitter radiation [292, 293], observational selection biases [274] and/or time-dependent acceleration and radiation [275], where low-pitch angle diffusion can also explain high energy indices steeper than predicted by isotropic scattering. Other models invoke a photospheric component and pair formation [310], see below.

There has been extensive work indicating that the apparent clustering of the break energy of prompt GRB spectra in the 50-500 keV range may be real [381], rather than due to observational selection effects [375]. I.e. the question is, if this is a real clustering, what is the physical reason for it. (Note, however, that if X-ray flashes, or XRF, discussed below, form a continuum with GRB, then this clustering stretches out to much lower energies; at the moment, however, the number of XRFs with known break energies is small). Since the synchrotron peak frequency observed is directly dependent on the bulk Lorentz factor, which may be random, the question arises whether this peak is indeed due to synchrotron, or to some other effect. An alternative is to attribute a preferred peak to a black-body at the comoving pair recombination temperature in the fireball photosphere [106]. In this case a steep low energy spectral slope is due to the Rayleigh-Jeans part of the photosphere, and the high energy power law spectra and GeV emission require a separate explanation. For such photospheres to occur at the pair recombination temperature in the accelerating regime requires an extremely low baryon load. For very large baryon loads, a related explanation has been invoked [465], considering scattering of photospheric photons off MHD turbulence in the coasting portion of the outflow, which up-scatters the adiabatically cooled photons up to the observed break energy.

Pair formation can become important [404, 362, 374] in internal shocks or dissipation regions occurring at small radii, since a high comoving luminosity implies a large comoving compactness parameter

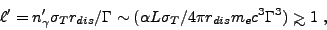(24)

where 1 is the luminosity fraction above the electron rest mass. Pair-breakdown may cause a continuous rather then an abrupt heating and lead to a self-regulating moderate optical thickness pair plasma at sub-relativistic temperature, suggesting a comptonized spectrum [164]. Copious pair formation in internal shocks may in fact extend the photosphere beyond the baryonic photosphere value (18). A generic model has been proposed [310, 312, 390, 426, 427, 394] which includes the emission of a thermal photosphere as well as a non-thermal component from internal shocks outside of it, subject to pair breakdown, which can produce both steep low energy spectra, preferred breaks and a power law at high energies. A moderate to high scattering depth can lead to a Compton equilibrium which gives spectral peaks in the right energy range [364, 365]. An important aspect is that Compton equilibrium of internal shock electrons or pairs with photospheric photons lead to a high radiative efficiency, as well as to spectra with a break at the right preferred energy and steep low energy slopes [406, 366, 367]. It also leads to possible physical explanations for the Amati [8] or Ghirlanda [160] relations between spectral peak energy and burst fluence [406, 464].

4.8. Alternative Prompt Emission Models

There are several alternative models for the prompt GRB emission, which so far have not found wide use for explaining the observations. The most plausible of these, despite the technical difficulties which impair its applicability, considers the main -ray burst emission to arise from magnetic reconnection or dissipation processes, if the ejecta is highly magnetized or Poynting dominated [468, 465, 304, 306, 102, 279, 464]. The central engine could also in principle be a temporary highly magnetized neutron star or magnetar [508]. These scenarios would lead to alternative dissipation radii, instead of equation (17), where reconnection leads to particle acceleration, and a high radiative efficiency is in principle conceivable due to the very high magnetic field. An external shock would follow after this, whose radius in the "thin shell" limit would be again given by equation (15), with a standard forward blast wave but no (or a weaker) reverse shock [304, 305], due to the very high Alfvén speed in the ejecta. For a long duration outflow, however, the dynamics and the deceleration radius would be similar to the "thick shell" case of Section 4.6, i.e. the case with a relativistic reverse shock [279]. Following the claim of an observed high gamma-ray polarization in the burst GRB 021206 [72], there was increased attention on such models for some time (e.g. [279]), and on whether the usual baryonic (i.e. sub-dominant magnetization) jets might also be able to produce such high polarization [499, 177, 179, 322, 280, 255, 107, 89]. The issue may remain unresolved, as the observational analysis appears to be inconclusive [423, 71, 511].

Other alternative models include different central energy sources such as strange stars ([65, 33, 101, 348]) and charged black hole electric discharges [421], while retaining essentially similar fireball shock scenarios. A model unifying SGR, XRF and GRB [115, 116] postulates a very thin (10^-4 rad) precessing, long-lived magnetized jet. This requires a separate explanation for the light-curve ("jet") breaks, and the interaction during precession with the massive stellar progenitor is unclear. Another speculative radiation scenario considers non-fluid ejecta in the form of discrete "bullets" [193], or "cannon-balls" ejected at relativistic velocities, which assume no collective interactions (i.e. no collisionless shocks) and instead rely on particle-particle interactions, and produce prompt emission by blue-shifted bremsstrahlung and produce afterglows by IC scattering progenitor or ambient photons [77, 89]. The predictions are similar to those of the standard fluid jet with shocks or dissipation. However, the basic ansatz of coherent bullet formation, acceleration to relativistic velocities and their survival against plasma instabilities is an unanswered issue in this model. It is also farther from astrophysical experience, whereas other well-observed systems such as AGN jets, which are known to be fluid (as is almost everything else in astrophysics at high energy per particle values) involve dynamical and radiation physics concepts which are quite plausibly extended to the GRB context. Fluid or plasma GRB outflow and jet models are better supported by theoretical work and simulations, and are so far not only compatible with observations but have produced predictions borne out by observations. Nonetheless, even in this standard scenario, the models remain largely phenomenological. The detailed nature of the underlying central engine and progenitor are poorly known, and the micro-physics of particle acceleration, magnetic field amplification in shocks and/or reconnection or dissipation is not well understood, and the radiation mechanisms are, at least for the prompt emission, subject of discussion.