


The structure, dynamics and evolution of a wind can be described by the equations of radiation magnetohydrodynamics. Possible wind driving mechanisms can be identified in the equation of motion:
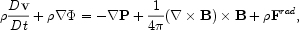 |
(1) |
where  ,
v, P, and B is the gas mass
density, velocity, gas pressure, and magnetic field, respectively.
The terms Frad and
,
v, P, and B is the gas mass
density, velocity, gas pressure, and magnetic field, respectively.
The terms Frad and
 in the equation of motion are
the total radiation force per unit mass and the gravitational potential,
respectively.
in the equation of motion are
the total radiation force per unit mass and the gravitational potential,
respectively.
To produce an outflow, there must be a force or forces which can overcome gravity. The terms in the right hand side of eq. 1 correspond to three possible forces: (1) the gradient of gas pressure, (2) the Lorentz force, and (3) the radiation force (which results from gradient of radiation pressure). Each of these forces can produce a wind. Here, I will describe how and under what physical conditions these forces can be stronger than gravity. I consider a Keplerian accretion disk, which is initially in a hydrostatic equilibrium (HSE), i.e., near the equatorial plane the gradient of gas pressure balances gravity in the vertical direction.
A disk in HSE can lose its mass if the upper atmosphere is heated. In the context of an AGN disk, significant heating can result from irradiation of the outer/cooler parts of the disk by the radiation from the inner/hotter disk. Theoretical models predict that heating, especially X-ray heating, can have significant effects on the gas dynamics in disks. X-rays tend to heat low density gas, through Compton heating, to a high temperature of ~ 107 K (the so-called Compton temperature). With such a high temperature, an upper disk atmosphere is expected to either puff up and form a static corona, or to produce a thermal wind, depending on whether the thermal velocity exceeds the local escape velocity, vesc (e.g., Begelman, McKee and Shields, 1983; Ostriker, McKee, & Klein 1991; Woods et al. 1996; Proga & Kallman 2002). Because vesc is a function of radius, for a given temperature of the heated gas, the effects of thermal driving depend to the radius, too. Generally, thermal driving is effective at large radii where vesc is small and one expects such winds to be responsible for low velocity X-ray absorption features in AGN spectra (e.g., Chelouche & Netzer 2005).
Thermal driving is likely less important for temperatures below 107 K because the other two forces can dominate. In particular, radiation forces can be significant for the gas with the temperatures < 105 K.
2.2. Radiation Pressure Driving
In the case of a fully ionized gas, radiation pressure is only due to electron scattering. Therefore, the system luminosity would have to be higher than the Eddington luminosity, LEdd if radiation driving is to be dynamically important. However, the radiation force can overcome gravity even for sub-Eddington sources provided the gas opacity is higher than the electron scattering, e.g., for the gas temperature < 105 K. The gas opacity can be enhanced via bound-bound and bound-free transitions.
I will illustrate radiation driving by describing the radiation
force on spectral lines (line force) because a line-driven disk wind
is the most promising hydrodynamical (HD) scenario for
AGN outflows. The presence of the BALs themselves
strongly indicates that substantial momentum is transfered from
a powerful radiation field to the gas.
A crucial clue to the origin of AGN outflows comes from the discovery
of line-locking in BAL QSO spectra (e.g.,
Foltz et al. 1987).
Weymann et al. (1991)
discovered that a composite spectrum
of their BAL QSO sample shows a double trough in the C IV
 1549 BAL, separated in
velocity space by the N V
1549 BAL, separated in
velocity space by the N V
 1240-Ly
1240-Ly splitting ~
5900 km s-1 (see also
Korista et al. 1993).
In fact Arav & Begelman
(1994,
see also
Arav et al. 1995
and Arav 1996)
showed that an absorption hump in the C IV
splitting ~
5900 km s-1 (see also
Korista et al. 1993).
In fact Arav & Begelman
(1994,
see also
Arav et al. 1995
and Arav 1996)
showed that an absorption hump in the C IV
 BAL is "the ghost
of Ly
BAL is "the ghost
of Ly " due to modulation
of the radiation force by the
strong emission in Ly
" due to modulation
of the radiation force by the
strong emission in Ly .
.
Line force can be significant, provided that the gas is moderately ionized and can interact with the UV continuum through very many UV line transitions (Castor, Abbott & Klein 1975, CAK hereafter). For gas photoionized by the UV radiation in the optically thin case, the total line opacity compared to the electron scattering (the so-called CAK force multiplier) can be as high as Mmax ~ 2000 - 4000 (e.g., CAK; Owocki, Castor & Rybicki 1988). For highly ionized gas, line force is inefficient because of a lower concentration of ions capable of providing UV line opacity (Mmax drops to zero).
In the radiation disk wind scenario, a wind is launched from the disk by the local disk radiation at radii where the disk radiation is mostly in the UV (Shlosman, Vitello & Shaviv 1985; MCGV). Such a wind is continuous and has mass loss rate and velocity which are capable of explaining the blueshifted absorption lines observed in many AGN, if the ionization state is suitable. This wind scenario has the important feature that it does not rely on difficult to measure forces or fields - such as magnetic fields - for their motive power.
UV driven disk winds in AGN are motivated by analogy with winds from hot stars, which have been explored in great detail (e.g., Lamers and Cassinelli 1999 and references therein). However, stars differ from disks in important ways, including the role of rotation near a Keplerian disk, the non-uniform disk temperature distribution, and the influence of the strong X-ray flux from the inner disk and black hole (the X-rays can overionize the gas). The wind density and mass loss rate can be estimated from the UV observations of AGN. When compared with the X-ray flux from the AGN, the density is low enough that the gas is predicted to be highly ionized. If so, the opacity needed for efficient driving and for line formation will be very small and line driving would be negligible. On the other hand, the column density in the radial direction close to the disk surface are high enough that a portion of the wind can be shielded from this ionization.
Viable models for disk winds must account self-consistently for the wind driving, ionization, and self shielding. MCGV pointed this out and postulated the existence of `hitchhiking' gas which is not driven by UV but which provides the shielding. They demonstrated the role of this shield gas on a one-dimensional, time independent quasi-radial flow. Proga, Stone & Kallman (2000, PSK hereafter; see also Proga & Kallman 2002, PK hereafter) were able to relax some of the MCGV assumptions, and explored consequences of a radiation driven disk wind model by performing two-dimensional, axisymmetric, time-dependent HD simulations. In PSK's simulations, self-consistent HD was coupled with radiative driving, ionization balance and radiative transfer. The main results from the simulations is the fact that if one allows the disk wind to be two-dimensional, the shielding material can be self-consistently produced as a simple consequence of the multi-dimensional nature of the problem.
I emphasize that, within the framework of line driving, X-ray shielding is necessary for an observer to see AGN outflows in UV absorption lines and for the outflows to be accelerated. Assuming a steady state radial outflow and imposing total momentum conservation, one can show that unshielded gas outflowing with high velocities has too high a photoionization parameter to produce UV lines and to be driven by the line force. This result holds for an outflow consisting of a continuous wind as well as for an outflow consisting of dense clouds. The latter needs shielding from X-rays if the filling factor decreases with increasing radius. A need for some shielding of clouds has been already hinted at in the literature (e.g., de Kool & Begelman 1995).
To avoid overionization without shielding, a wind which is launched by a force other than the line force (and other than thermal driving) must be denser than the wind predicted by the line-driven wind models by several orders of magnitude. Thus if AGN outflows are unshielded and launched from an accretion disk at relatively large distances from the central object (where the local line force due to the disk is negligible) then we have to figure out not only what mechanism launches this dense outflow but also what mechanism accelerates the outflow to velocities much higher than vesc from the location of the launch (e.g., Arav, Li & Begelman 1994). The result that shielding of the wind from the X-rays is required regardless of the filling factor of the line-driven outflow is consistent with the observed anti-correlation for QSOs between the relative strength of the soft X-ray flux and the C IV absorption equivalent width (e.g., Brandt, Laor, & Wills 2000).
Thus, the importance of line driving in quasars and in some other AGN has been demonstrated in specific studies of this type of systems. However, based on physical arguments as well as numerical simulations one can show that radiation driven disk winds are produced when LUV > LEdd / Mmax, where LUV is the system UV luminosity (e.g., Proga et al. 1998, PSD hereafter). Moreover, one can argue that in all accretion disks, with the UV luminosity, LUV > a few 10-4 LEdd, mass outflows have been observed (Proga 2002 and fig. 2 there). For example, accretion disks around: massive black holes, white dwarfs (respectively as in AGN and cataclysmic variable, with LUV > 0.001 LEdd) and low mass young stellar objects (as in FU Ori stars with LUV > a few 0.01 LEdd ) show fast winds. Systems that have too low UV luminosities to drive a wind include accretion disks around neutron stars and low mass black holes as in low mass X-ray binaries and galactic black holes. These systems indeed do not show outflows similar to those observed in AGN, cataclysmic variables, and FU Ori (see Miller et al. 2006, for an example of a disk wind in a X-ray binary which is likely magnetically driven).
Radiation seems to drive an outflow mainly for most luminous
and massive AGN.
PK have performed simulations of radiation driven disk winds
for a range of the disk luminosities, LD
and black hole masses, MBH.
In all explored cases, the disk atmosphere can 'shield' itself from
external X-rays
so that the local disk radiation can launch gas off the disk
photosphere. However, this gas is not always accelerated
to become a wind. In particular, for
MBH = 108
M of a
typical quasar and
LD > 0.3 LEdd, a strong disk wind
develops whereas for LD
of a
typical quasar and
LD > 0.3 LEdd, a strong disk wind
develops whereas for LD
 0.3
LEdd there is no wind.
For a less luminous disk or stronger ionizing radiation that reduces
Mmax, or both, the line force can still lift gas off
the disk but it fails to accelerate it.
Such a failed disk wind has been
found in simulations with but also without X-ray ionization (see PSD for
no X-ray cases, runs 1 and 6 there).
Additionally, the disk wind solution is sensitive to
MBH: for a fixed ratio, LD /
LEdd it is easier to produce a wind for
MBH
0.3
LEdd there is no wind.
For a less luminous disk or stronger ionizing radiation that reduces
Mmax, or both, the line force can still lift gas off
the disk but it fails to accelerate it.
Such a failed disk wind has been
found in simulations with but also without X-ray ionization (see PSD for
no X-ray cases, runs 1 and 6 there).
Additionally, the disk wind solution is sensitive to
MBH: for a fixed ratio, LD /
LEdd it is easier to produce a wind for
MBH
 107
M
107
M than for
MBH
than for
MBH
 107
M
107
M .
However, when a wind develops, the synthetic
line profiles predicted by the radiation driven models are consistent
with BALs observed in quasars (PK).
.
However, when a wind develops, the synthetic
line profiles predicted by the radiation driven models are consistent
with BALs observed in quasars (PK).
The fact that radiation driving is successful only for high MBH and LD is an important result and its implications need to be explored (e.g., Proga 2005). One of the implications is of course that radiation driving is not enough to explain all AGN. In fact, some studies show that not all AGN outflows appear to be driven by radiation (e.g., Chelouche & Netzer 2005; Kraemer et al. 2006). This brings us to the third and last force that is important in driving winds: the Lorentz force.
Magnetic effects must be important in AGN, in fact, they appear to be essential for the existence of all accretion disks. The magnetorotational instability (MRI, Balbus & Hawley 1991) has been shown to be a very robust and universal mechanism to produce turbulence and transport angular momentum in disks at all radii (Balbus & Hawley 1998; see also Ji et al. 2006). It is therefore likely that magnetic fields control mass accretion inside the disk and play a key role in producing a mass outflow from the disk.
There are two classes of magnetically driven winds: (1) magnetocentrifugal winds where the dominant contribution to the Lorentz force is the magnetic tension and (2) magnetic pressure driven winds where the dominant contribution to the Lorentz force is the magnetic pressure.
Blandford & Payne
(1982;
see also
Pelletier & Pudritz
1992)
showed that the centrifugal force can
drive a wind from the disk if the poloidal component of the magnetic
field, Bp makes an angle of > 30° with respect
to the normal to the disk surface. Generally, magnetocentrifugal disk winds
require the presence of a sufficiently
strong, large-scale, ordered magnetic field threading the disk
with a poloidal component at least comparable to the toroidal magnetic
field, |B / Bp|
/ Bp|
 1 (e.g.,
Cannizzo & Pudritz
1988,
Pelletier & Pudritz
1992).
Several groups have studied
numerically outflows using this mechanism (e.g.,
Ustyugova et al. 1995,
1999;
Romanova et al. 1997;
Ouyed & Pudritz 1997a,
1997b,
1999;
Krasnopolsky, Li &
Blandford 1999;
Kato, Kudoh & Shibata
2002).
An important feature of magnetocentrifugal winds is that they require
some assistance to flow freely and steadily from the surface of the
disk, to pass through a slow magnetosonic surface (e.g.,
Blandford & Payne
1982).
Thus magnetocentrifugal wind models predict the geometry
and kinematics of the winds but they do not predict the mass-loss rate
but rather assume it.
Therefore these models can not be completely tested against observations.
1 (e.g.,
Cannizzo & Pudritz
1988,
Pelletier & Pudritz
1992).
Several groups have studied
numerically outflows using this mechanism (e.g.,
Ustyugova et al. 1995,
1999;
Romanova et al. 1997;
Ouyed & Pudritz 1997a,
1997b,
1999;
Krasnopolsky, Li &
Blandford 1999;
Kato, Kudoh & Shibata
2002).
An important feature of magnetocentrifugal winds is that they require
some assistance to flow freely and steadily from the surface of the
disk, to pass through a slow magnetosonic surface (e.g.,
Blandford & Payne
1982).
Thus magnetocentrifugal wind models predict the geometry
and kinematics of the winds but they do not predict the mass-loss rate
but rather assume it.
Therefore these models can not be completely tested against observations.
Many favor magnetocentrifugal winds as an explanation for the outflows in young stellar objects and in some AGN (e.g., Blandford & Payne 1982; Uchida & Shibata 1985; Emmering, Blandford & Shlosman 1992; Contopoulos & Lovelace 1994; Bottorff et al. 1997; Bottorff, Korista & Shlosman 2000). Magnetic winds do not require radiation pressure and thus can be important in low luminosity systems such as young stellar objects and systems where gas can be overionized by very strong radiation as in AGN (e.g., Königl & Kartje 1994; Ouyed & Pudritz 1997; Ustyugova et al. 1999; Krasnopolsky, Li & Blandford 1999, and references therein). In the context of AGN outflows, models usually rely on the effects of magnetic fields as well as on line driving (Königl & Kartje 1994, de Kool & Begelman 1995, Everett, Königl, & Arav 2002; Proga 2003a; Everett 2005).
For example, within the framework proposed by de Kool and Begelman (1995, see also Everett 2005) a wind is launched from an outer cold disk. Such a wind is made of dense clouds confined by the magnetic field, and therefore does not require shielding. The wind is accelerated by the UV radiation emitted from the inner disk. The wind may be but does not have to be equatorial and can produce spectral features for all inclination angles provided there is at least one cloud in the line of sight.
One of the differences between magnetocentrifugal and radiation driven disk winds is that the former corotate with the disk, at least close to the disk, whereas the latter do not. A key parameter shaping the total line profile made up of both scattered emission and absorption is the ratio of the expansion velocity to the rotational velocity (e.g., Proga 2003b). Corotating winds, conserve the gas specific angular velocity and therefore have a higher rotational velocity than those which do not corotate and conserve the gas specific angular momentum. The former also have higher terminal velocities due to stronger centrifugal force. Additionally in the wind where the specific angular velocity is conserved the rotational velocity is comparable to the terminal velocity while in the wind where the specific angular momentum is conserved the rotational velocity decreases asymptotically to zero with increasing radius and is therefore much lower than the terminal velocity (Proga 2000). Thus we should be able to distinguish these two kinds of winds based on their line profiles. For example, highly rotating winds should produce emission lines much broader than slowly rotating, expanding winds, if we see the disk edge-on. Line absorption should also be changed that corotation. One should hope that synthetic line profiles predicted by models of magnetocentrifugal winds will soon be computed so that we will be able to compare these two types of winds.
Wind corotation depends on the strength of Bp. For a
relatively weak Bp, a wind may corotate only very
close to the disk and be
driven by the magnetic pressure instead of the magnetic tension.
In particular, the toroidal magnetic field can quickly build up inside
the disk due to the differential rotation of the disk so that
|B / Bp| >> 1.
In such a case, the magnetic pressure of the toroidal field can give rise
to a self-starting wind (e.g.,
Uchida & Shibata 1985;
Pudritz & Norman 1986;
Shibata & Uchida 1986;
Stone & Norman 1994;
Contopoulos 1995;
Kudoh & Shibata 1997;
Ouyed & Pudritz 1997b).
/ Bp| >> 1.
In such a case, the magnetic pressure of the toroidal field can give rise
to a self-starting wind (e.g.,
Uchida & Shibata 1985;
Pudritz & Norman 1986;
Shibata & Uchida 1986;
Stone & Norman 1994;
Contopoulos 1995;
Kudoh & Shibata 1997;
Ouyed & Pudritz 1997b).
To our best knowledge, the first numerical simulations of the two-dimensional, time-dependent magnetohydrodynamical (MHD) structure of line-driven winds from luminous accretion disks were presented in Proga (2003a). In these simulations, the disk was initially threaded by a purely axial magnetic field. This study was focused on a generic disk wind problem and did not include strong ionizing radiation. This approach is relevant to AGN outflows because it addresses, for example, the problem of a wind produced beyond a shielding region, i.e., the outer outflow. The simulations showed that the magnetic field very quickly starts deviating from purely axial due to MRI. This leads to fast growth of the toroidal magnetic field as field lines wind up due to the disk rotation. As a result the toroidal field dominates over the poloidal field above the disk and the gradient of the former drives a slow and dense disk outflow, which conserves specific angular momentum of fluid. Depending on the strength of the magnetic field relative to the system luminosity the disk wind can be radiation- or MHD-driven. The pure line-driven wind consists of a dense, slow outflow that is bounded on the polar side by a high-velocity stream. The mass-loss rate is mostly due to the fast stream. As the magnetic field strength increases first the slow part of the flow is affected, namely it becomes denser and slightly faster and begins to dominate the mass-loss rate. In very strong magnetic field or pure MHD cases, the wind consists of only a dense, slow outflow without the presence of the distinctive fast stream which is a very characteristic feature of line-driven winds. Winds launched by the magnetic fields are likely to remain dominated by the fields downstream because of their relatively high densities. Line driving may not be able to change a dense MHD wind because the line force strongly decreases with increasing density.