


The preceding sections suggest that the bulk of GCs formed at high redshift. It then follows that they have enormous promise in a cosmological context. In this section we discuss current ideas on the "cosmological" formation of GCs and how this has shaped our overall view of galaxy formation. In what follows, the term cosmological refers to models in which GCs form in low-mass dark matter halos, before the bulk of their parent galaxy has been assembled.
Soon after CDM cosmology was proposed, Peebles (1984) argued that
108
M halos,
each hosting a few × 106
M
halos,
each hosting a few × 106
M of
gas, would be the first to collapse and form stars in the early
universe. He suggested GCs as their progeny, and noted that the halos of
these GCs might be stripped without disrupting the cluster itself. This
basic idea has been sustained to the present day, though the mechanism
is probably limited to metal-poor GCs.
Rosenblatt, Faber, & Blumenthal (1988)
refined this scenario by suggesting that metal-poor
GCs form in 2.8
of
gas, would be the first to collapse and form stars in the early
universe. He suggested GCs as their progeny, and noted that the halos of
these GCs might be stripped without disrupting the cluster itself. This
basic idea has been sustained to the present day, though the mechanism
is probably limited to metal-poor GCs.
Rosenblatt, Faber, & Blumenthal (1988)
refined this scenario by suggesting that metal-poor
GCs form in 2.8 halos. This gives a reasonable match to the observed radial distribution
of metal-poor Galactic GCs and the mass fraction of metal-poor GCs (with
respect to total stellar mass) in a variety of galaxies. The principal
problem with this picture - indeed, of GC formation in individual dark
matter halos in general - is that the minimum required baryonic collapse
factor (~ 10 or more) would produce GCs with more rotation than that
observed, unless they form preferentially in very low-spin halos, or
some other mechanism acts to remove angular momentum. A speculative
solution might be to form the GC in the core of a larger gas cloud, if
the "extraneous" material can be stripped later.
halos. This gives a reasonable match to the observed radial distribution
of metal-poor Galactic GCs and the mass fraction of metal-poor GCs (with
respect to total stellar mass) in a variety of galaxies. The principal
problem with this picture - indeed, of GC formation in individual dark
matter halos in general - is that the minimum required baryonic collapse
factor (~ 10 or more) would produce GCs with more rotation than that
observed, unless they form preferentially in very low-spin halos, or
some other mechanism acts to remove angular momentum. A speculative
solution might be to form the GC in the core of a larger gas cloud, if
the "extraneous" material can be stripped later.
Moore (1996) wrote a short influential paper that described the use of N-body simulations to show that the faint tidal tails observed around some GCs (Grillmair et al. 1995) were inconsistent with the presence of extended dark matter halos, but consistent with the low M/L ratios observed in the central regions (e.g., Illingworth 1976; Pryor et al. 1989). The observed tidal tails around, e.g., Pal 5 (Odenkirchen et al. 2002) demonstrate that there are at least some present-day GCs that lack dark matter. However, this does not prove that all (or even most) GCs are free of extended dark matter halos, nor does it rule out metal-poor GC formation inside halos that are later stripped away.
This latter idea has been developed in a number of papers by Mashchenko & Sills (2005a, b), who studied the formation and evolution of GCs with individual dark matter halos. With high-resolution N-body simulations, they found that (depending on the details of the actual collapse) many properties of simulated GCs with halos are similar to those of observed GCs. For example, the central mass-to-light ratios are expected to be quite low. Structure in the halo (e.g., triaxiality, or breaks in the outer parts of the density profile) could easily be manifested as tidal cutoffs, extratidal stars, or eccentric outer contours; such features are not incompatible with the presence of dark matter. When a GC with a dark matter halo evolves in a tidal field, their simulations indicated that it loses either most (for an NFW halo) or nearly all (for a Burkert halo) of its dark matter. This finding was confirmed in a very high resolution dark matter and gas simulation by Saitoh et al. (2005).
Bromm & Clarke (2002)
used a simulation with both dark matter and
gas to study GC formation at high redshift. As noted by
Peebles (1984),
~ 108
M minihalos are expected to collapse out of
3
minihalos are expected to collapse out of
3 fluctuations at z ~
15. At a high fixed gas density threshold Bromm & Clarke created
sink particles as "GCs". These GCs initially form inside of halos, but
the simultaneous collapse of mass scales results in violent relaxation
that erases most of the substructure. The resulting GC mass spectrum is
set by that of the dark matter, and is a power law with index ~
-1.8. The main problem here is that it is not possible to tell, with the
current level of sophistication of their simulations, whether the
violent relaxation is real or merely an artifact of insufficient
resolution.
fluctuations at z ~
15. At a high fixed gas density threshold Bromm & Clarke created
sink particles as "GCs". These GCs initially form inside of halos, but
the simultaneous collapse of mass scales results in violent relaxation
that erases most of the substructure. The resulting GC mass spectrum is
set by that of the dark matter, and is a power law with index ~
-1.8. The main problem here is that it is not possible to tell, with the
current level of sophistication of their simulations, whether the
violent relaxation is real or merely an artifact of insufficient
resolution.
Other authors have explored in more detail the triggering mechanism for
putative GC formation in dark matter halos. In the model of
Cen (2001),
ionization fronts from cosmic reionization shock gas in low-mass
halos. The gas is compressed by a factor ~ 100 and collapses to form
metal-poor GCs. To produce the observed numbers of GCs, a large
population of low spin
( < 0.01) halos is
required. This
condition appears to be satisfied when the halo number density is
modeled with extended Press-Schecter theory, but whether it would hold
in high-resolution cosmological simulations is unknown. This model
predicts a power law GCMF with a slope of ~ -2, similar to that observed
at the high mass end, and has the rather attractive property of
predicting no GC mass-radius relation, consistent with the observations.
Côté (2002)
pointed out that this picture could
predict a large number of (unobserved) intergalactic GCs; this objection
might be addressed if the ionization fronts are effective above a
threshold only met quite close to protogalaxies.
< 0.01) halos is
required. This
condition appears to be satisfied when the halo number density is
modeled with extended Press-Schecter theory, but whether it would hold
in high-resolution cosmological simulations is unknown. This model
predicts a power law GCMF with a slope of ~ -2, similar to that observed
at the high mass end, and has the rather attractive property of
predicting no GC mass-radius relation, consistent with the observations.
Côté (2002)
pointed out that this picture could
predict a large number of (unobserved) intergalactic GCs; this objection
might be addressed if the ionization fronts are effective above a
threshold only met quite close to protogalaxies.
Scannapieco et al. (2004) proposed a somewhat similar mechanism, in which gas in minihalos is shock-compressed by galaxy outflows. The momentum of the shock strips the gas from the halo, nicely solving the dark matter problem. However, this model predicts a mass-radius relation for individual GCs, and the observed lack of such a relation may deal this picture a fatal blow.
Ricotti (2002) suggested that GCs themselves could have reionized the universe. The predicted number of ionizing photons appears to be sufficient, assuming that the escape fraction of such photons is near unity. Such a high escape fraction is qualitatively feasible, given the extended spatial distribution of the GCs with respect to their parent galaxies, but the scenario requires detailed modeling (including radiative transfer) in the proper cosmological setup.
The high-resolution simulation of Kravtsov & Gnedin (2005) offers a glimpse of what should be possible in the future. They performed a gas and dark matter simulation of the formation of a Milky Way analogue to z ~ 3. They were not able to resolve GC formation directly, but assumed GCs formed in the cores of GMCs when the dynamical time exceeded the cooling time. These GMCs were located in the flattened gas disks of protogalaxies. The resulting mass function appears to be consistent with that of massive GCs, but the metallicity distribution does not: at the end of the simulation, large numbers of (unobserved) [Fe/H] ~ -1 GCs were being formed, even though their simulation included feedback. A desirable future extension of such simulations is to test whether reionization might effectively end metal-poor GC formation where "traditional" stellar feedback cannot.
Moore et al. (2006)
have shown that the observed radial distribution of
metal-poor GCs in the Galaxy can be reproduced if the GCs are assumed to
form in  2.5
2.5 peaks of
peaks of
 2 ×
108
M
2 ×
108
M that
collapse and form stars before z ~ 12 (see
Figure 14). If the key assumption of truncation
by reionization is
supported by other evidence, then the surface density distributions of
metal-poor GCs could be used to probe reionization in a variety of
galaxies, setting limits on the epoch and homogeneity of reionization.
that
collapse and form stars before z ~ 12 (see
Figure 14). If the key assumption of truncation
by reionization is
supported by other evidence, then the surface density distributions of
metal-poor GCs could be used to probe reionization in a variety of
galaxies, setting limits on the epoch and homogeneity of reionization.
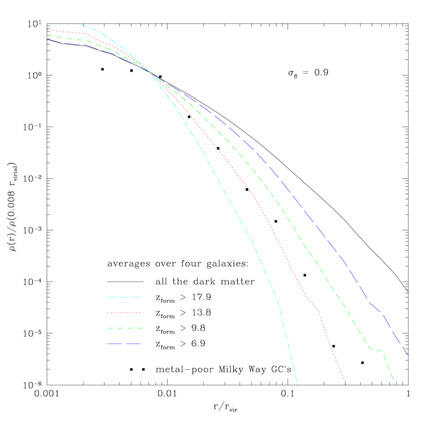 |
Figure 14. The radial distribution of
metal-poor GCs in the Galaxy compared to results from
numerical simulations of the formation of a Galaxy-like dark matter
halo in a |
In summary, the cosmological formation of metal-poor GCs is supported by
several lines of argument. (i) The ages of metal-poor GCs. The absolute
ages of GCs are still poorly known, and must be continually revised in
light of advances in a variety of subfields (for example, the recent
revision of the 14N(p,
 )15O reaction rate increases GC ages by 0.7-1 Gyr;
Imbriani et al. 2004).
If the GC
ages are sufficiently close to the age of the universe, cosmological
formation becomes a necessity, since low-mass halos as described above
are the only existing sites for star formation. (ii) The recently
discovered correlation between GC metallicity and mass for bright
metal-poor GCs in several massive galaxies
(Strader et al. 2006;
Harris et al. 2006).
Self-enrichment is a potential explanation for this
correlation, and it is possible that metals could only be retained in
the potential well of a dark matter halo. (iii) The radial distribution
of metal-poor GCs.
Moore et al. (2006)
show that the metal-poor GCs in
the Galaxy have a radial distribution consistent with formation in
2.5
)15O reaction rate increases GC ages by 0.7-1 Gyr;
Imbriani et al. 2004).
If the GC
ages are sufficiently close to the age of the universe, cosmological
formation becomes a necessity, since low-mass halos as described above
are the only existing sites for star formation. (ii) The recently
discovered correlation between GC metallicity and mass for bright
metal-poor GCs in several massive galaxies
(Strader et al. 2006;
Harris et al. 2006).
Self-enrichment is a potential explanation for this
correlation, and it is possible that metals could only be retained in
the potential well of a dark matter halo. (iii) The radial distribution
of metal-poor GCs.
Moore et al. (2006)
show that the metal-poor GCs in
the Galaxy have a radial distribution consistent with formation in
2.5 peaks in the dark
matter distribution at z > 12. (iv) Observations of Local
Group dwarfs show that the lowest-mass galaxies with GCs have total
masses of
peaks in the dark
matter distribution at z > 12. (iv) Observations of Local
Group dwarfs show that the lowest-mass galaxies with GCs have total
masses of  108
M
108
M (see
Section 10), as expected under cosmological
formation.
(see
Section 10), as expected under cosmological
formation.
Does this mean that two separate mechanisms are needed to explain metal-poor and metal-rich GC formation? The strongest similarity between the two subpopulations is their mass function; for the less evolved high-mass part of the mass function, these are approximately power laws with indices ~ -1.8 to -2. Since power law distributions are a consequence of a variety of physical processes, this similarity does not mandate an identical formation history for both subpopulations. For example, the power law slope observed in the GC mass function is the same as both that of GMCs in the Galaxy and of low-mass dark matter halos collapsing at z ~ 15-20.