


The present-day appearance of a GC is a complicated convolution of the initial conditions of its formation with subsequent internal and external dynamical effects. The surface brightness distributions of GCs are reasonably well-fit by single-mass King (1966) models. These form a dimensionless one-parameter family as a function of the concentration c = rt / r0 (where rt is the tidal radius and r0 is the scale radius). In dimensionless form, the half-light radius (rh-"size") is a monotonic function of c, and is the only one of these three radii that is relatively unaffected by dynamical evolution (Spitzer 1987; Meylan & Heggie 1997) and can serve as a probe of GC formation conditions.
A correlation between rh and galactocentric radius (R) for Galactic GCs was discovered by van den Bergh et al. (1991). This could not be explained by dynamical evolution of the GC system, since diffuse inner GCs might be expected to be destroyed, but compact distant GCs should (if they existed) have remained intact. Thus, this result represents strong evidence for some degree of in situ formation of Galactic GCs.
HST/WFPC2 imaging of NGC 3115 and M87 revealed that metal-poor GCs are ~ 20% larger than metal-rich GCs (Kundu & Whitmore 1998; Kundu et al. 1999). This was confirmed statistically in many early-type galaxies by Larsen et al. (2001) and Kundu & Whitmore (2001a). Explanations offered for this result have included:
(i) It represents an intrinsic formation difference, e.g., the metal-rich GCs formed in a higher-pressure environment.
(ii) It is a results of projection effects. Since the metal-rich GC spatial distribution is more centrally concentrated than that of the metal-poor GCs, within some given projected radius the metal-rich GCs will tend to lie at smaller R. If there is a strong correlation between size and R (as in the Galaxy), the metal-rich GCs will appear smaller on average than the metal-poor GCs (Larsen & Brodie 2003). This model predicts that size differences will be largest in the inner parts of galaxies and disappear in the outer regions.
(iii) It is a natural outcome of assuming metal-poor and metal-rich GCs have the same half-mass radii. Since the brightest stars in metal-rich GCs are more massive than in metal-poor GCs, mass segregation leads to a more compact distribution and a smaller half-light radius (Jordán 2004). In this model there should be little change in the relative sizes with galactocentric distance.
Option (i) is not testable at present, so should be left as a fallback only if the other possibilities can be eliminated. Regarding (ii), Larsen & Brodie (2003) showed that the rh - R correlation in the Galaxy could explain all of the observed size differences between the metal-poor and metal-rich GCs. However, in order to explain the ~ 20% size difference in external galaxies, steep rh - R relations would be required, and the radial distribution of the GCs would need to have a central core like a King profile (this appears to be consistent with observations). Model (iii) has a number of critical assumptions upon which its conclusions depend, including identical GC ages and initial mass functions. Small changes in either of these parameters (e.g., an age difference of ~ 2 Gyr between the metal-poor and metal-rich GCs) could erase most of the expected size difference. Jordán (2004) also used equilibrium King-Michie models to represent the GCs; full N-body modeling is a desirable next step. In Figure 10, taken from Jordán (2004), we show the sizes of GCs in M87 together with a best-fit model of type (iii).
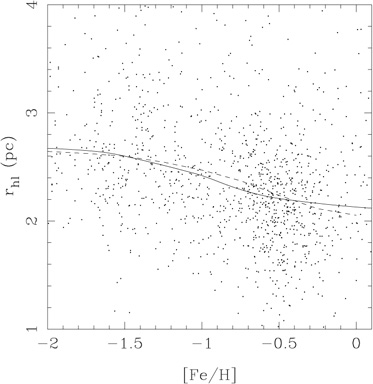 |
Figure 10. Half-light radii of GCs in M87 vs. [Fe/H] (derived from g - z color). The overplotted solid and dashed lines are a running robust mean and a model fit (based upon King models; Jordán 2004) normalized to the metal-poor GCs. As is typical in massive galaxies, the metal-rich GCs are smaller than the metal-poor GCs (figure courtesy A. Jordán). |
Several recent observational results have provided important new constraints. Jordán et al. (2005) studied GC sizes in 67 early-type galaxies with a wide range of luminosity from the ACS Virgo Cluster Survey (Côté et al. 2004). For bright metal-poor GCs they found a significant but rather shallow relationship between rh and projected R (normalized to the effective radius of the galaxy). In log space the value of the slope is 0.07, compared to ~ 0.30 for a similar sample of Galactic GCs. They did not list the fits for individual galaxies, and there are clearly variations, but the bulk of the galaxies do not appear to have rh - R relations as steep as observed in the Galaxy, so projection effects on the GC subpopulation sizes should be small, and option (ii) is not favored. They also found that GCs in bluer/fainter host galaxies tend to be slightly larger. Despite these variations, rh is still relatively constant among galaxies. Thus, with their observed correlations between rh and galaxy properties, they were able to calibrate rh as a distance indicator, as suggested by Kundu & Whitmore (2001a).
Wide-field HST/ACS data for NGC 4594 (covering ~ 6' × 10') do not appear consistent with option (iii), however. Spitler et al. (2006) found that the ratio of metal-poor to metal-rich GC sizes declines steeply and steadily from ~ 1.25 in the center to ~ 1 at the edge of the complete observations. Thus it appears that, at least in NGC 4594, projection effects account for most of the observed size differences.
It seems clear from these results that both projection and segregation mechanisms can play a role in determining the sizes observed for extragalactic GCs. Since each is sensitive to the physical conditions of the GC system, galaxies will need to be studied on an individual basis to determine which effects are important. Particularly valuable would be high-resolution, wide-field imaging of GC systems, like the HST/ACS mosaic of NGC 4594 discussed above.