1.6. FUTURE CHALLENGES

1.6.1. Disks

The claim that there is no strong theoretical support for the disks to be exponential (Böker et al. 2003) is partly substantiated by the fact that theories are often tuned so as to reproduce an exponential light profile. While reproducing exponential light profiles is considered to be a test for viable models of disk formation (e.g., Dalcanton, Spergel, & Summers 1997; Silk 2001), it is certainly true that most of the current disk models and simulations do predict large mass fractions with low-angular momentum material that is in excess of the extrapolation of the outer exponential density distribution to the center (see Section 1.1 and references therein). However, the real problem is to understand whether this excess low-angular momentum material does remain in the disk, or rather forms a three-dimensional bulge.

Furthermore, it is also possible that, rather than being born denser than exponential, the disks may become so during the subsequent galactic evolution. Indeed many processes can occur during the Hubble time that can transform exponential disks into the more complex structures that are observed in late-type disks. In this context, it is worth stressing that a third of the late-type disks remais well described by the simple single-exponential form, showing that this channel of disk formation is indeed accessible to real galaxies.

An obvious example of change in central concentration in disks is the one induced by the formation and subsequent buckling of a stellar bar. To study at unprecedented resolution the effects of secular evolution processes on the central regions of disks, we are conducting state-of-the-art N-body and N-body+SPH numerical simulations of disk galaxies (details will be published in Debattista et al. 2003 and Mayer et al. 2003). The first N-body experiments that I briefly discuss here (from Debattista et al. 2003) consist of live disk components inside frozen halos described either by a spherical logarithmic potential with a central core or a cuspy Hernquist (1990) potential. The initially axisymmetric disks are modeled assuming an exponential profile with a Gaussian thickening; the disks are represented by (4 - 7.5) × 10⁶ equal-mass particles. The spatial resolution that is achieved in the central regions is ~ 50 pc. The simulations are run on a 3-D cylindrical polar-grid code (described in Sellwood & Valluri 1997). In certain areas of parameter space, the axisymmetric systems are found to be unstable and form bars. Systems in which bars fail to form have only modest heating, indicating that our results are not driven by noise. Every 20 time steps of the disk evolution, we measure the disk velocity dispersions and streaming velocities in annuli, the amplitude of the bar from the m = 2 Fourier moment, and the amplitude of the buckling from the m = 2 Fourier moment of the vertical displacement of particles. We use these quantities to determine when the bar forms, when it buckles, and the evolution of disk properties such as mass density, morphological diagnostics (for any inclination angle of the disk and orientation of the bar), and the V / ratio. As an example, Figure 1.1 shows, for various disk inclination angles and tilt angles of the bar with respect to the disk major axis, the isophotal contours of the projected surface density of the system after the bar has formed and buckled. As already pointed out in, for example, Raha et al. (1991), for some projections, including but not uniquely for the edge-on one, the buckled bar looks very much like a normal (three-dimensional) "rounder-than-the-disk" bulge. Figure 1.2 shows, for two different simulations, how the systems would appear on the sky as observed from a specific line-of-sight before and after the buckling of the bars. For the same two models, Figure 1.3 plots the initial surface density profiles (exponential by construction), the surface density profiles after the buckling of the bars, and the post-buckling ellipticity profiles of the systems. Figure 1.3 points out that an initially exponential disk that "nature" makes can be observed to be a more centrally concentrated structure at a later stage, after it has formed and buckled a stellar bar. The final, post-buckling profile in the simulations is well described by the sum of an outer exponential disk and an inner Sérsic component, as observed in real disk galaxies. If the denser-than-exponential profiles in the real late-type spirals were due to the effects of nurture rather than nature, the inner light/mass excesses in the late-type disks would be better associated with "bulge" structures; that is, they would be the "bulges" produced by secular evolution of the disks, which has been extensively discussed in the literature.

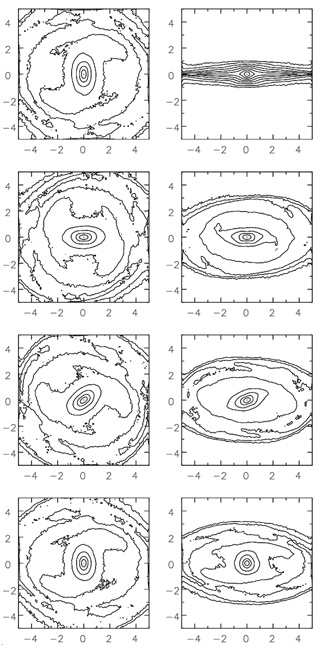Figure 1.1. Contour plots for a live-disk/frozen-halo simulation after the development and buckling of a stellar bar. The halo has a Hernquist (1990) profile; the disk initially has a single-exponential profile. Shown are the face-on and edge-on views of the system (upper panels, left and right, respectively), and two different views with disk inclination angles of 30° (left) and 60° (right), respectively. Different panels from second-top to bottom show different orientation angles for the buckled bar of 0°, 45°, and 90°, respectively, with respect to the major axis of the disk. Axes are in units of the initial exponential disk scale length. (From Debattista et al. 2003.)

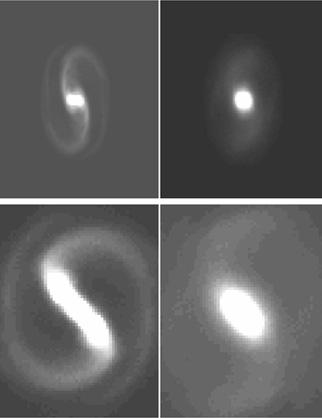Figure 1.2. A Hernquist halo simulation (upper panels) and a core halo simulation (lower panels). The images are taken before the buckling (left panels) and after the buckling (right panels) of the bars. The models have inclination angles of 60° and 30°, and bar orientation angles of 90° and 45°, respectively. (From Debattista et al. 2003.)

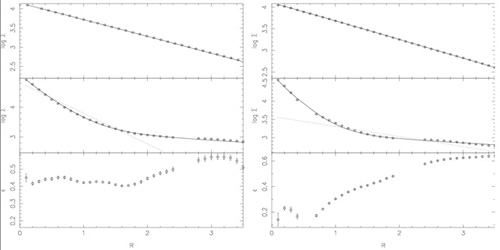Figure 1.3. For the same core halo (left) and Hernquist halo (right) models shown in Figure 1.2, we plot here the initial surface density profiles (upper panels: superimposed with the single-exponential fits), the surface density profiles after buckling (middle panels: dotted lines, the single exponential fits; solid lines, exponential plus Sérsic fits), and the ellipticity profiles after buckling (lower panels). The x-axis is in units of the initial exponential disk scale length. (From Debattista et al. 2003.)

Bars are not the only possible solution to increase the central densities in disk galaxies by means of processes that occur after the original baryonic collapse inside the dark halos: viscosity may be important (e.g., Lin & Pringle 1987), and also mergers, satellite accretion, dynamical friction of globulars, etc. Nonetheless, it is fair to conclude that, at this stage, the issue whether the disks are born as denser-than-exponential structures remains open. If this were the case, it will be important to quantify the systematic uncertainties on, for example, bulge scale lengths and luminosities, black hole masses and other galactic properties that are derived assuming that nature, when it makes a disk, makes it exponential.

1.6.2. Bulges

The investigations of the past few years indicate that even the most massive, early-type bulges are not r^1/4-law systems and have disklike imprints in their kinematics. How do we reconcile, under a common denominator, the differences between bulges and ellipticals with the quoted similarities of stellar population and scaling laws? It is certainly not clear what, for instance, the Mg₂ index and the velocity dispersion represent in the Mg₂ - relation. Are the key parameters metallicity, age, or a combination of the two? Are they the depth of potential well, local physics of star formation, or, again, a combination of the two? Local physics imposes thresholds for star formation (e.g., Meurer et al. 1997), which is likely to have an impact on scaling laws such as the Mg₂ - relation. Indeed, the same Mg₂ - relation is observed to hold over orders of magnitude of scale lengths, in systems that are very different, ranging from elliptical galaxies to dwarf spheroidals (Bender, Burstein, & Faber 1993). The conclusion is that the Mg₂ - and similar relations are certainly telling us something important about the formation of stellar systems over a large range of scales, but not necessarily that they all share a similar formation process.

On the other hand, the claims that violent relaxation is not a major player in the formation of bulges, based on the observed Sérsic profiles with n 3 (Balcells et al. 2003) may also be premature. The consequence of violent relaxation during dissipationless processes such as stellar clumpy collapses (van Albada 1982), mergers of disk galaxies (Barnes 1988), satellite accretion onto disk galaxies (Aguerri, Balcells, & Peletier 2001) is to produce an r^1/4 profile. However, other studies of violent relaxation in a finite volume show deviations from the r^1/4 law (Hjorth & Madsen 1995). Furthermore, the same problem of separating nature from nurture may be relevant also in this context. Physical processes may occur during the Hubble time that modify the stellar density profiles in the centers of galaxies, including dynamical friction of globular clusters, dissipative accretion of matter, black hole-driven cusp formation, mergers of black holes (quantitative studies of the latter show that central mass deficits are created from the binding energy liberated by the coalescence of the supermassive binary black holes; see, e.g., Milosavljevic et al. 2002, Ravindranath, Ho, & Filippenko 2002, and references therein). Numerical studies of these processes are still rather sketchy and do not explore a vast volume of parameter space; nonetheless, they make the point that the nuclear stellar density profiles may be modified by subsequent evolution. Quantitative work remains to be done to assess whether these or other processes can reproduce the n 3 Sérsic profiles typical of the massive bulges and the weak trend between Sérsic shape parameter n and bulge luminosity. The possibility that the disks may not be purely exponential also introduces additional uncertainties on the derived bulge parameters, including the shape index n. If the outer disk can have a Sérsic shape with n values as steep as ~ 2.5, bulge-disk decompositions that use an exponential for the outer disks can systematically offset the bulge parameters. This could even open the question as to whether the observed sequence in n values between the late-type and early-type bulges is a pure bulge sequence, or, rather, at least in part a sequence of different underlying disk profiles.

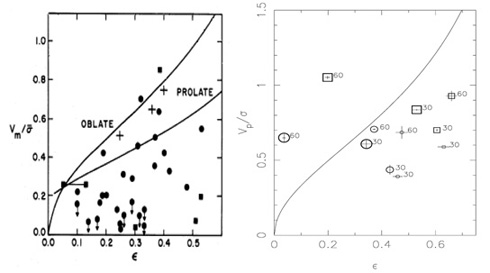Figure 1.4. V / versus ellipticity plane. The left panel reproduces Figure 2 of Davies & Illingworth (1983); points are the measurements for observed spheroids, both bulges (crosses), and ellipticals (filled circles and squares). The right panel shows a similar plot derived from our simulations. The oblate-rotator line is also plotted as a solid line. The data points in this panel refer to the end of the simulations, after the bars that have formed in the disks have buckled. The V / and values for the "buckled bars" are derived by averaging the relative profiles inside the half-light radii of the inner Sérsic components that are necessary, in addition to the outer exponential disk components, to obtain good fits to the surface density profiles after buckling. Circles are used for the logarithmic and squares for the Hernquist halo potentials. The size of the symbols refers to the bar orientation angles (90° largest, 45° intermediate, 0° smallest). The disk inclination angle i is explicitly indicated close to symbols. From certain viewing angles and bars orientation angles, buckled bars are indistinguishable from normal spheroids on the V / versus ellipticity plane. (From Debattista et al. 2003.)

Concerning support for bulge-building secular evolution processes inside preexisting disks, there is certainly at this point good evidence from high-resolution numerical experiments that the intrinsic evolution of the disks results in transformations of the disks, which can generate three-dimensional structures that resemble bulgelike components. Numerical studies (Pfenniger & Friedli 1991; Zhang & Wyse 2000; Scannapieco & Tisseira 2003; Debattista et al. 2003, see Fig. 1.3) also show that the bulgelike, three-dimensional structures that generally result from the evolution of the disks have the rather low-n Sérsic profiles typical of real bulges. MacArthur et al. (2003) report that simulations by D. Pfenniger (2002, private communication) of self-gravitating disks form bars that may later dissolve into bulgelike components, which show a nearly universal ratio of bulge-to-disk scale lengths, also in agreement with the observed correlations. In the simulations, the universal ratio of bulge-to-disk scale lengths is related to the stellar dynamics of the barred system, for example to the relative position of the vertical to horizontal resonances. There is an additional important ingredient that has been missing so far in the debate concerning the possibility that disk secular evolution processes play a substantial role in forming bulgelike structures: namely, the bulges that result from the secular evolution of the disks are, in contrast to what is commonly asserted, not necessarily dynamically cold, "disklike" stellar systems. Due to the fact that eccentric orbits are quickly erased by shocks (Friedli & Benz 1995), the secular evolution of mostly gaseous disks indeed produces cold stellar structures such as the pseudo-bulges discussed by Kormendy (1993); however, the buckling of stellar bars, for example, can produce structures that are, at least from certain viewing angles, indistinguishable from the alleged "normal" bulges in classical diagnostic planes such as the V / - plane. This is shown in Figure 1.4, where the locations on the V / - of a few representative buckled bars from our simulations are shown (right panel) in comparison with what is typically considered the bona fide bulge behavior (left panel, figure from Davies & Illingworth 1983).

In summary, from Figures 1.1-1.4, it is evident that, depending on the viewing angle, buckled bars can appear as structures that are simultaneously rounder than the surrounding disks, photometrically identifiable as additional components in excess of outer exponential disks, and kinematically similar to what are considered to be "bona fide bulges." In this light, it seems appropriate to question indeed what is a meaningful definition for a bona fide bulge. Clearly, the situation is more complex than what is captured in the theorist-versus-observer dichotomy discussed by Böker et al. (Section 1.4). First, from an observational perspective, even early-type, bona fide bulges have been claimed to be thickened disks (Falcón-Barroso et al. 2003). Second, from a theoretical perspective, evolutionary disk processes such as the buckling of progenitor bars inside the disks can produce structures that, in contrast to common belief, are dynamically similar to the bona fide bulges that should be the benchmark for the comparison. Thus, as with the photometric classification, even the kinematic classification of bulges is quite fuzzy. Ultimately, this is due to the lack of a proper physical boundary between structures that are forced into different categories by what may be unfolding into an obsolete and confusing classification scheme.

1.6.3. The Nature and Role of Nuclei and Central Black Holes

Recent surveys show that central, distinct, compact components, in addition to the disk and the bulge, are present in the large majority of disk galaxies of all Hubble types. Many are clearly star clusters with no AGN contamination. This includes, for example, the "naked" ones in the late-type disks studied by Walcher et al. (2003) and probably the relatively faint population of nuclei embedded in the relatively clean surroundings of the exponential-type bulges (Carollo et al. 1997a, 1998). AGNs are known to be rare in late-type galaxies (Ho, Filippenko, & Sargent 1997; Ulvelstad & Ho 2002; Ho 2003). An AGN component may, however, be present in a fraction of the nuclei. This would be statistically consistent with the fact that about 70% of spirals host a distinct nucleus, and about half of them are known to host some form of AGN, even if weak (Ho et al. 1997). Some of the point sources embedded in the early-type bulges of Balcells et al. (2003) may also have an AGN origin or component; pointlike sources associated with AGNs are seen in massive elliptical galaxies (Carollo et al. 1997b, c; Ravindranath et al. 2001).

The young stellar ages plus high velocity dispersions of the central star clusters of late-type disks reported by Walcher et al. (2003) may certainly imply a large spread in stellar population ages, and thus an iterative mass assembly and star formation for the central star clusters, as discussed by the authors. However, the nuclei that are typically selected for the spectroscopic investigations populate the bright end of the luminosity distribution of nuclei. Walcher et al. (2003) stress that in their sample there is no indication that brighter means younger; nevertheless, it is still possible that selection effects are important and that fainter nuclei may have less complex mass assembly and star formation histories. A wide range of star formation histories would be more consistent with a process of growth of central star clusters that is regulated by local physics, for instance by the amount of fuel (either gas or smaller star clusters) available at various epochs in the circumnuclear regions, the angular momentum distribution or orbital structure of this "fuel," and the physical state of the central regions of the disk (e.g., its density or dynamical temperature, in turn determining or originating from the steepness of the gravitational potential, the conditions to develop non-axisymmetric perturbations on small scales, etc.). Furthermore, it is still unknown whether fuel-starved, silent AGN engines - massive black holes - may be present in the central star clusters (e.g., Marconi et al. 2003). The question of whether massive black holes reside in general in the centers of star clusters is far from settled. The case of G1, a globular cluster in Andromeda in which a central black hole of the mass expected from the linear extrapolation of the relationship reported for the massive spheroids (e.g., Gebhardt et al. 2000) has been detected (Gebhardt, Rich, & Ho 2002), argues for the presence of massive black holes in the centers of star clusters, and supports the suggestion that black holes are ubiquitous and proportionally sized in all spheroids, from mass scale of globular clusters to elliptical galaxies. A small, ~ 10^4-5 M black hole is found embedded in the central star cluster of NGC 4395, one of the least luminous and nearest known Type 1 Seyfert galaxies (Filippenko & Ho 2003). On the other hand, the nondetection of a central black hole in the central star cluster of M33 contrasts with the G1 case and argues for the absence of massive black holes in the centers of the distinct nuclei of bulgeless disks. Gebhardt et al. (2001) discuss that, if the mass of a central black hole in the nucleus of M33 was related to its velocity dispersion in the same way that the known supermassive black holes are related to the dispersions of their bulges, then a black hole with mass in the range ~ 7 × 10³ - 6 × 10⁴ M would be expected, well above the measured upper limit of 1500 M. Solutions to this inconsistency include those suggested by the authors: the relationship between the mass of the black hole and the velocity dispersion of the host spheroid may be nonlinear; the conditions to make a massive black hole were better in the earlier, denser Universe, when the stars in G1 were made; or M33's young nucleus has not had enough time to create its own black hole. Given the observational uncertainties, other possibilities remain. It could be that G1 is not a star cluster but a harassed spheroidal galaxy [a fact mentioned by Gebhardt et al. (2002) but not considered by the authors as the cause for the discrepancy]. Another possibility is that at least in small-sized spheroids such as star clusters, black holes may not be ubiquitous, or there may not exist a tight correlation between black hole mass and spheroid mass. Or perhaps normal star clusters and the central star clusters in disk galaxies have a different origin.

The case of M33 serves also as a smoking gun in another context. Kormendy & Gebhardt (2001; see also Kormendy et al. 2003) report that the same correlation between the mass of the central black hole and the host luminous spheroid holds for galaxies with both "normal" and kinematically cold, disklike bulges (i.e., the "pseudobulges" discussed by Kormendy 1993). In contrast, M33, a pure disk galaxy with no bulge component of any sort, is indeed found to lack a black hole. Kormendy & Gebhardt (2001) conclude that the basic requirement for making a supermassive central black hole appears to be that the galaxy is capable of forming some kind of dense, bulgelike structure, whatever its nature. Reinterpreting this comment in the light of the bulge/dense-disk conundrum discussed above, the results of Kormendy & Gebhardt (2001) and Gebhardt et al. (2001) may imply that the requirement for making a supermassive central black hole is that the galaxy is capable of reaching sufficiently high central baryonic densities. Either way, from these analyses it appears that black hole masses are not correlated with the total gravitational potential of the disks, and thus of the host dark matter halos. A contrasting report, however, comes from Ferrarese (2002) and Baes et al. (2003), who claim a tight correlation between the circular velocities of galaxies and the masses of their central supermassive black holes, and thus an intimate link between the black holes and the host dark matter halos. Supermassive black holes do form in some pure disk systems, as shown by Filippenko & Ho (2003) for the case of NGC 4395. However, these authors stress that in this galaxy the estimated black hole mass is consistent with the M - relation of Tremaine et al. (2002), if the central cluster is considered in lieu of the bulge. For a = 30 km s^-1, a good upper limit for the velocity dispersion of central star cluster in NGC 4395, this relation predicts a M = 6.6 × 10⁴ M, consistent with the mass independently estimated from the AGN properties (Filippenko & Ho 2003). Furthermore, it remains a fact that M33, possibly the best candidate to test for the validity of a correlation between the black hole mass and the dark matter halo mass, appears not to support it. As stressed by Gebhardt et al. (2001), if a black hole in M33 were indeed related to the dark matter potential well, then M33 should contain a black hole of mass significantly in excess of 10⁶ M, which it does not. It may be best to wait for the observational picture to be cleared up before attempting interpretations of the claimed correlation between black hole and dark halo masses.

Finally, given the large frequency of occurrence of nuclei in disk galaxies and the generally accepted idea of hierarchical galaxy assembly, an interesting question is whether the formation and evolution of the nuclei of disk galaxies play any relevant role in the formation of supermassive black holes in the centers of galaxies. More generally, a key question for the future is whether the nearly ubiquitous nuclei are a nuance or rather an important ingredient in the formation process of disk galaxies.