2. AN OVERVIEW OF PRIMORDIAL NUCLEOSYNTHESIS

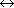The early (0.6 1 ms), hot, dense Universe is filled with radiation (s, e ^± pairs, s of all flavors), along with dynamically and numerically insignificant amounts of baryons (nucleons) and dark matter particles. Nuclear and weak interactions are occurring among the neutrons, protons, e ^± , and s (e.g., n + p D + ; p + e^- n + _e) at rates fast compared to the universal expansion rate. At such high temperatures (T 3 MeV), in an environment where the nucleon to photon ratio is very small (₁₀ 3 - 10), the abundances of complex nuclei (D, ³He,⁴He, ⁷Li) are tiny in comparison to those of the free nucleons (neutrons and protons). At the same time, the charged-current weak interactions are regulating the neutron to proton ratio, initially keeping it close to its equilibrium value

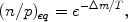(13)

where m is the neutron - proton mass (energy) difference. In this context it is worth noting that if there is an asymmetry between the numbers of _e and _e the equilibrium neutron-to-proton ratio is modified to (n / p)_eq = exp(-m / T - µ_e / T) = e^-_e(n / p)_eq⁰.

As the Universe expands and cools, the lighter protons are favored over the heavier neutrons and the neutron-to-proton ratio decreases, tracking the equilibrium form in eq. 13. But, as the temperature decreases below T ~ 0.8 MeV, when the Universe is ~ 1 second old, the weak interactions are too slow to maintain equilibrium and the neutron-to-proton ratio, while continuing to fall, deviates from (exceeds) the equilibrium value. Since the n / p ratio depends on the competition between the weak interaction rates and the early-Universe expansion rate (as well as on a possible neutrino asymmetry), deviations from the standard model (e.g., _{R R} + _X or _e 0) will change the relative numbers of neutrons and protons available for building the complex nuclides.

As noted above, while neutrons and protons are interconverting, they are also colliding among themselves creating complex nuclides, e.g., deuterons. However, at early times, when the density and average energy of the CBR photons are very high, the newly formed deuterons find themselves bathed in a background of high-energy gamma rays capable of photodissociating them. Since there are more than a billion CBR photons for every nucleon in the Universe, the deuteron is photodissociated before it can capture a neutron (or a proton, or another deuteron) to build the heavier nuclides. This bottleneck to BBN persists until the temperature drops sufficiently below the binding energy of the deuteron, when there are too few photons energetic enough to photodissociate them before they capture nucleons, launching BBN. This transition (smooth, but rapid) occurs after e ^± annihilation, when the Universe is a few minutes old and the temperature has dropped below ~ 80 keV.

Once BBN begins in earnest, neutrons and protons quickly combine to build D, ³H, ³He, and ⁴He. Since there are no stable mass-5 nuclides, a new bottleneck appears at ⁴He. Nuclear reactions quickly incorporate all available neutrons into ⁴He, the most strongly bound of the light nuclides. Jumping the gap at mass-5 requires Coulomb suppressed reactions of ⁴He with D, or ³H, or ³He, guaranteeing that the abundances of the heavier nuclides are severely depressed below that of ⁴He (and even of D and ³He), and that the ⁴He abundance is determined by the neutron abundance when BBN begins. The few reactions that manage to bridge the mass-5 gap lead mainly to mass-7 (⁷Li or, to ⁷Be which, later, when the Universe has cooled further, will capture an electron and decay to ⁷Li); for the range of _B of interest, the BBN-predicted abundance of ⁶Li is more than 3 orders of magnitude below that of the more tightly bound ⁷Li. Finally, there is another gap at mass-8, ensuring that there is no astrophysically significant production of heavier nuclides.

The primordial nuclear reactor is short-lived. As the temperature drops below T 30 keV, when the Universe is ~ 20 minutes old, Coulomb barriers abruptly suppress all nuclear reactions. Afterwards, until the first stars form, no pre-existing, primordial nuclides are destroyed (except for those like ³H and ⁷Be that are unstable and decay) and no new nuclides are created. In ~ 1000 seconds BBN has run its course.

With this as background, the trends of the SBBN-predicted primordial abundances of the light nuclides with baryon abundance shown in Figure 1 can be understood. The reactions burning D and ³He (along with ³H) to ⁴He are very fast (compared to the universal expansion rate) once the deuterium bottleneck is breached, ensuring that almost all neutrons present at that time are incorporated into ⁴He. As a result, since ⁴He production is not rate limited, its primordial abundance is very insensitive (only logarithmically) to the baryon abundance. The very slight increase in Y_P with increasing _B reflects the fact that for a higher baryon abundance BBN begins slightly earlier, when slightly more neutrons are available. The thickness of the Y_P curve in Fig. 1 reflects the very small uncertainty in the BBN prediction; the uncertainty in Y_P (~ 0.2%; _Y ~ 0.0005) is dominated by the very small error in the weak interaction rates which are normalized by the neutron lifetime (_n = 885.7 ± 0.8 s). The differences among the Y_P predictions from independent BBN codes are typically no larger than Y_P ~ 0.0002.

Figure 1. The SBBN-predicted primordial abundances of D, 3He, 7Li (relative to hydrogen by number), and the 4He mass fraction (YP), as functions of the baryon abundance parameter 10. The widths of the bands reflect the uncertainties in the nuclear and weak interaction rates.

Nuclear reactions burn D, ³H, and ³He to ⁴He, the most tightly bound of the light nuclides, at a rate which increases with increasing nucleon density, accounting for the decrease in the abundances of D and ³He (the latter receives a contribution from the -decay of ³H) with higher values of _B. The behavior of ⁷Li is more interesting, reflecting two pathways to mass-7. At the relatively low values of ₁₀ 3, mass-7 is largely synthesized as ⁷Li by ³H(, )⁷Li reactions. ⁷Li is easily destroyed in collisions with protons. So, for low nucleon abundance, as _B increases, destruction is faster than production and ⁷Li/H decreases. In contrast, at relatively high values of ₁₀ 3, mass-7 is largely synthesized as ⁷Be via ³He(, )⁷Be reactions. ⁷Be is more tightly bound than ⁷Li and, therefore, harder to destroy. As _B increases at high nucleon abundance, the primordial abundance of ⁷Be increases. Later in the evolution of the Universe, when it is cooler and neutral atoms begin to form, ⁷Be captures an electron and -decays to ⁷Li. These two paths to mass-7 account for the valley shape of the ⁷Li abundance curve in Fig. 1.

Not shown on Figure 1 are the BBN-predicted relic abundances of ⁶Li, ⁹Be, ¹⁰B, and ¹¹B. Their production is suppressed by the gap at mass-8. For the same range in _B, all of them lie offscale, in the range 10^-20 - 10^-13.

For SBBN the relic abundances of the light nuclides depend on only one free parameter, the nucleon abundance parameter _B. As Figure 1 reveals, for the "interesting" range (see below) of 4 ₁₀ 8, the ⁴He mass fraction is expected to be Y_P 0.25, with negligible dependence on _B while D/H and ³He/H decrease from 10^-4 to 10^-5, and ⁷Li/H increases from 10^-10 to 10^-9. The light nuclide relic abundances span some nine orders of magnitude, yet if SBBN is correct, one choice of _B (within the errors) should yield predictions consistent with observations. Before confronting the theory with data, it is useful to consider a few generic examples of BBN in the presence of nonstandard physics and/or cosmology.

2.1. Nonstandard BBN

The variety of modifications to the standard models of particle physics and of cosmology is very broad, limited only by the creativity of theorists. Many nonstandard models introduce several, new, free parameters in addition to the baryon abundance parameter _B. Since there are only four nuclides whose relic abundance is large enough to be astrophysically interesting and, as will be explained below in more detail, only three for which data directly relating to their primordial abundances exist at present (D, ⁴He, ⁷Li), nonstandard models with two or more additional parameters may well be unconstrained by BBN. Furthermore, as discussed in the Introduction (see Section 1.2 and Section 1.3), there already exist two additional parameters with claims to relevance: the expansion rate parameter S (or, N; see eqs. 8, 11) and the lepton asymmetry parameter L (or, ; see eq. 12).

The primordial abundance of ⁴He depends sensitively on the pre- and the post-e ^± annihilation early universe expansion rate (the Hubble parameter H) and on the magnitude of a _e - _e asymmetry because each will affect the n/p ratio at BBN (see, e.g., Steigman, Schramm & Gunn 1977 (SSG) [6]; for recent results see Kneller & Steigman 2004 (KS) [9]) A faster expansion (S > 1; N > 0) leaves less time for neutrons to convert into protons and the higher neutron abundance results in increased production of ⁴He. For small changes at fixed _B, Y_P 0.16(S - 1) 0.013 N (KS). Although the relic abundances of D and ³He do depend on the competition between the nuclear reaction rates and the post-e ^± annihilation expansion rate (faster expansion less D and ³He destruction more D and ³He), they are much less sensitive to relatively small deviations from S = 1 ( N = 0) [9]. For mass-7 the effect of a nonstandard expansion rate is different at low and high values of _B. At low baryon abundance (₁₀ 3), a faster expansion leaves less time for ⁷Li destruction and the relic abundance of mass-7 increases. In contrast, at high baryon abundance (₁₀ 3), S > 1 leaves less time for ⁷Be production and the relic abundance of mass-7 decreases. As for D and ³He, the quantitative change in the ⁷Li abundance is small for small deviations from SBBN.

For similar reasons, Y_P is sensitive to an asymmetry in the electron neutrinos which, through the charged current weak interactions, help to regulate the n/p ratio. For _e > 0, there are more neutrinos than antineutrinos, so that reactions such as n + _e p + e^-, drive down the n/p ratio. For small asymmetry at fixed _B, KS find Y_P -0.23_e. The primordial abundances of D, ³He, and ⁷Li, while not entirely insensitive to neutrino degeneracy, are much less affected by a nonzero _e than is ⁴He (e.g., Kang & Steigman 1992 [10]).

Each of these nonstandard cases (S 1, 0) will be considered below. While certainly not exhaustive of the nonstandard models proposed in the literature, they actually have the potential to provide semi-quantitative, if not quantitative, understanding of BBN in a large class of nonstandard models. Note that data constraining the primordial abundances of at least two different relic nuclei (one of which should be ⁴He) are required to break the degeneracy between the baryon density and the additional parameter resulting from new physics or cosmology. ⁴He is a poor baryometer but a very good chronometer and/or, leptometer; D, ³He, ⁷Li have the potential to be good baryometers.

2.2. Simple - But Accurate - Fits To The Primordial Abundances

While BBN involves only a limited number of coupled differential equations, they are non-linear and not easily solved analytically. As a result, detailed comparisons of the theoretical predictions with the inferred relic abundances of the light nuclei requires numerical calculations, which may obscure key relations between abundances and parameters, as well as the underlying physics. In particular, the connection between the cosmological parameter set {_B, S, _e} and the abundance data set {y_D, Y_P, y_Li} ² may be blurred, especially when attempting to formulate a quantitative understanding of how the latter constrains the former. However, it is clear from Figure 1 that the relic, light nuclide abundances are smoothly varying, monotonic functions of _B over a limited but substantial range. While the BBN-predicted primordial abundances are certainly not linearly related to the baryon density (nor to the other parameters S and _e), over the restricted ranges identified above, KS [9] found linear fits to the predicted abundances (or, to powers of them) which work very well indeed. Introducing them here enables and simplifies the comparison of theory with data (below) and permits a quick, reasonably accurate, back of the envelope, identification of the successes of and challenges to BBN.

For the adopted range of _B, y_D = y_D(_B) is well fit by a power law,

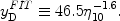(14)

While the true y_D - _B relation is not precisely a power law, this fit (for 4 ₁₀ 8) is accurate (compared to a numerical calculation) to better than 1%, three times smaller than the ~ 3% BBN uncertainty estimated by Burles, Nollett, Turner 2001 (BNT) [11]; this fit and the numerical calculation agree with the BNT result to 2% or better over the adopted range in _B. Note that since different BBN codes are largely independent and often use somewhat different nuclear reaction data sets, the differences among their predicted abundances may provide estimates of the overall uncertainties. It is convenient to introduce a "deuterium baryon density parameter" _D, the value of ₁₀ corresponding to an observationally determined primordial D abundance.

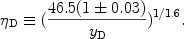(15)

Generalizing this to include the two other parameters, KS find

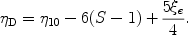(16)

This fit works quite well for 2 y_D 4, corresponding to 5 _D 7. In Figure 2 the deuterium isoabundance curves are shown in the S - ₁₀ plane, while Figure 3 shows the same isoabundance contours in the _e - ₁₀ plane. It is clear from Figures 2 and 3 that D is a sensitive baryometer since, for these ranges of S and _e, _{D 10}.

Figure 2. Isoabundance curves for Deuterium (dashed lines) and Helium-4 (solid lines) in the expansion rate factor (S) - baryon abundance (10) plane. The 4He curves, from bottom to top, are for YP = 0.23, 0.24, 0.25. The D curves, from left to right, are for yD = 4.0, 3.0, 2.0.

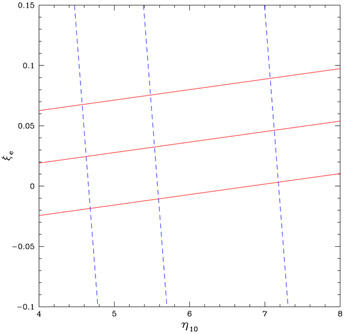Figure 3. As in Figure 2, in the neutrino asymmetry (e) - baryon abundance (10) plane. The 4He curves, from bottom to top, are for YP = 0.25, 0.24, 0.23. The D curves, from left to right, are for yD = 4.0, 3.0, 2.0.

Next, consider ⁴He. While over a much larger range in ₁₀, Y_P varies nearly logarthmically with the baryon density parameter, a linear fit to the Y_P versus ₁₀ relation is actually remarkably accurate over the restricted range considered here.

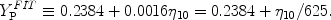(17)

Over the same range in ₁₀ this fit agrees with the numerical calculation and with the BNT [11] predictions for Y_P to within 0.0002 ( 0.1%), or better. Any differences between this fit and independent, numerical calculations are smaller (much smaller) than current estimates of the errors in the observationally inferred primordial value of Y_P. The following linear fits, including the total error estimate, to the Y_P - S and Y_P - _e relations from KS work very well over the adopted parameter ranges (see Figures 2 & 3).

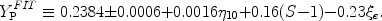(18)

As an aside, the dependence of the ⁴He mass fraction on the neutron lifetime (_n) can be included in eq. 18 by adding a term 0.0002(_n - 887.5), where _n is in seconds. A very recent, new measurement of _n by Serebrov et al. [12] suggests that the currently accepted value (_n = 887.5 s) should be reduced by 7.2 s. If confirmed, this would lead to a slightly smaller BBN-predicted ⁴He abundance: Y_P = -0.0014. The corresponding shift in the ⁴He inferred baryon density parameter is negligible compared to its range of uncertainty (_B / _B = -0.14), as is that for the shift in the upper bound to N (N^max = +0.11). These corrections are ignored here.

In analogy with the deuterium baryon density parameter introduced above, it is convenient to introduce _He, defined by

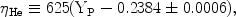(19)

so that

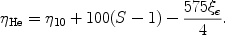(20)

For SBBN (S = 1 & _e = 0), _He is the value of ₁₀ corresponding to the adopted value of Y_P. Once Y_P is chosen, the resulting value of _He provides a linear constraint on the combination of ₁₀, S, and _e in eq. 20. This fit works well [9] for 0.23 Y_P 0.25, corresponding to -5 _He 7. As Figures 2 & 3 reveal, ⁴He is an excellent chronometer and/or leptometer, since the Y_P isoabundance curves are nearly horizontal (and very nearly orthogonal to the deuterium isoabundance curves).

As with D, the ⁷Li abundance ³ is well described by a power law in ₁₀ over the range in baryon abundance explored here: y_Li 10¹⁰(Li/H) ₁₀². The following KS fit agrees with the BBN predictions to better than 3% over the adopted range in ₁₀,

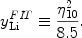(21)

While this fit predicts slightly smaller lithium abundances compared to those of BNT [11], the differences are at the 5-8% level, small compared to the BNT uncertainty estimates as well as those of Hata et al. (1995) [13] (~ 10 - 20%).

In analogy with _D and _He defined above, the lithium baryon abundance parameter _Li (allowing for a 10% overall uncertainty) is defined by

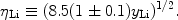(22)

The simple, linear relation for _Li as a function of ₁₀, S, _e, which KS find fits reasonably well over the adopted parameter ranges is,

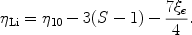(23)

This fit works well for 3 y_Li 5, corresponding to 5 _Li 7, but it breaks down for y_Li 2 (_Li 4); see Fig. 1. As is the case for deuterium, lithium can be an excellent baryometer since, for the restricted ranges of S and _e under consideration here, _{Li 10}.

Finally, it may be of interest to note that for ³He the power law y₃ - _B relation, where y₃ 10⁵(³He/H), which is reasonably accurate for 4 ₁₀ 8 is

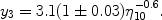(24)

The difficulty of using current observational data, limited to chemically evolved regions of the Galaxy, to infer the primordial abundance of ³He, along with the relatively weak dependence of y₃ on ₁₀, limits the utility of this nuclide as a baryometer [14]. ³He can, however, be used as a test of BBN consistency.

2.3. SBBN-Predicted Primordial Abundances

Before discussing the current status of the observationally determined abundances (and their uncertainties) of the light nuclides, it is interesting to assume SBBN and, for the one free parameter, _B, use the value inferred from non-BBN data such as the CBR (WMAP) and Large Scale Structure (LSS) [2] to predict the relic abundances.

From WMAP alone, Spergel et al. 2003 [2] derive ₁₀ = 6.3 ± 0.3. Using the fits from Section 2.2, with S = 1 and _e = 1, the SBBN-predicted relic abundances are: y_D = 2.45 ± 0.20; y₃ = 1.03 ± 0.04; Y_P = 0.2485 ± 0.0008; y_Li = 4.67 ± 0.64 ([Li]_P = 2.67 ± 0.06).

When Spergel et al. 2003 [2] combine the WMAP CBR data with those from Large Scale Structure, they derive a consistent, but slightly smaller (slightly more precise) baryon abundance parameter ₁₀ = 6.14 ± 0.25. For this choice the SBBN-predicted relic abundances are: y_D = 2.56 ± 0.18; y₃ = 1.04 ± 0.04; Y_P = 0.2482 ± 0.0007; y_Li = 4.44 ± 0.57 ([Li]_P = 2.65_-0.06^+0.05).

² Y_P is the ⁴He mass fraction while the other abundances are measured by number compared to hydrogen. For numerical convenience, y_D 10⁵(D/H) and y_Li 10¹⁰(Li/H). Back.

³ It is common in the astronomical literature to present the lithium abundance logarithmically: [Li] 12 + log(Li/H) = 2 + log(y_Li). Back.