3. COULOMB RELAXATION OF TEMPERATURES IN THE WHIM

3.1. Relaxation of the ion temperature anisotropy

A plasma flow partly randomised just behind the viscous ion jump in a collisionless shock transition has an anisotropic velocity distribution with respect to the mean magnetic field. In Fig. 1 the oxygen phase densities in the v_x - x and v_y - x projections transverse to the mean field have a substantially wider distribution than that in the projection v_z - x parallel to the magnetic field. In many cases the ion velocity distributions (like that in Fig. 2 right) can be approximated with a quasi-Maxwellian distribution introducing some effective kinetic temperature (more exactly it is the second moment of the distribution). Then the parallel and perpendicular (to the mean field) temperatures are different and we approximate the 3D particle distribution as

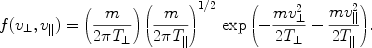(4)

We will measure the temperatures in energy units in most of the equations below (thus k_B T T). Ichimaru & Rosenbluth (1970) (see also a comment by Kaiser 1979) obtained the following equation to describe the ion anisotropy relaxation

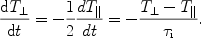(5)

Here

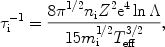(6)

where ln is the Coulomb logarithm and the effective ion temperature is defined as

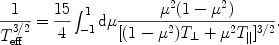(7)

These equations were obtained under the assumption that the electrons have no dynamical role, but provide a static dielectric background to the ions. We can directly apply Eqs. 5 - 7 to isotropisation of the plasma field particles (i.e. protons in our case). Isotropisation of the minor ion components is mainly due to their interactions with protons and helium because of a low metal number density in cosmic plasma.

3.2. Relaxation of the ion and electron temperatures

Following shock heating and the temperature isotropisation a quasi-Maxwellian distribution will be established within all plasma components, i.e. groups of identical particles, after a time scale given by Eq. 6. The effective temperatures differs strongly between the components. All the plasma particles will undergo Coulomb collisions with the protons, alpha particles and electrons dominating the WHIM plasma, resulting in the temperature equilibration. Spitzer (1962) found that the temperature relaxation of a test particle of type a with plasma field particles can be approximately estimated from

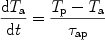(8)

where

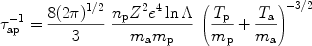(9)

In the thermal equilibrium state the postshock plasma must have a single equilibrium temperature T_eq. In a fully ionised plasma without energy exchange with external components (i.e. radiation or plasma wave dissipation) T_eq can be found from the condition of constant pressure in the plane shock downstream resulting in

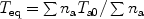(10)

In cosmic plasmas it is often a fair approximation to estimate T_eq from the equation 2T_eq = T_e + T_p. Then following Sivukhin (1966) the charged particle equilibration can be approximately described through the equation

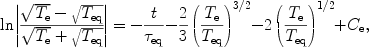(11)

where C_e is a constant to be determined from the initial temperature T_a0 of a relaxing component a = e, p,

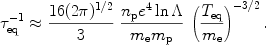(12)

Eq. 11 and Eq. 12 allow to calculate the structure of relaxation layers to be seen behind a collisionless shock in the WHIM. In Fig. 3 we illustrate the postshock equilibration of initially cold electrons with the protons initially heated at the ion viscous jump of a collisionless shock transition. The width of the ion viscous jump in cosmological shocks is negligible compared with the equilibration length x_eq = u_{2 eq}, where u₂ is the downstream flow velocity in the shock rest frame. The characteristic column density N_eq = n₂ x_eq to be traversed by protons and electrons in the downstream plasma (of a number density n₂) before the temperature equilibration, as it follows from Eq. 12, does not depend on the plasma number density, and N_eq v_sh⁴. The corresponding shocked WHIM column density can be expressed through the shock velocity v₇ measured in 100 km s^-1, assuming a strong shock where u₂ = v_sh / 4:

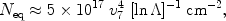or through the shocked WHIM gas temperature T₆ (measured in 10⁶ K):

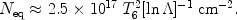The Coulomb logarithm for the WHIM condition is ln ~ 40. It follows from Fig. 3 that in the Coulomb relaxation model the postshock plasma column density N_H > 3 N_eq ensures the equilibration at a level better than 1%.

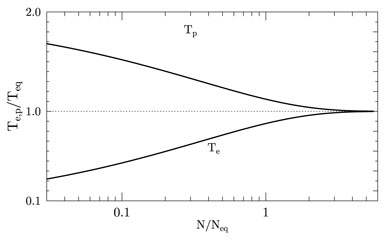Figure 3. Postshock temperature equilibration between the ion and electron components due to the Coulomb interactions.

The metal ions can be initially heated at the shock magnetic ramp to high enough temperatures > A T_p (see e.g. Korreck et al. 2007) for a recent analysis of interplanetary collisionless shock observations with Advanced Composition Explorer). However, in a typical case the depth N > 3 N_eq is enough for the ion temperature equilibration.

To study UV and X-ray spectra of the weak systems (N_HI < 10^12.5 cm^-2 and N_{O VII} < 10¹⁵ cm^-2) modelling of shocked filaments of N_H 10¹⁷ cm^-2 would require an account of non-equilibrium effects of low electron temperature T_e / T_eq < 1.

3.3. Effect of postshock plasma micro-turbulence on the line widths

We consider above only the WHIM temperature evolution due to the Coulomb equilibration processes. Shocks producing the WHIM could propagate through inhomogeneous (e.g. clumpy) matter. The interaction of a shock with the density inhomogeneities results in the generation of MHD-waves (Alfvén and magnetosonic) in the shock downstream (see e.g. Vainshtein et al. 1993). The MHD-wave dissipation in the shock downstream could selectively heat ions, being a cause of a non-equilibrium T_e / T_i ratio. In case of a strong collisionless shock propagating in a turbulent medium, cosmic ray acceleration could generate a spectrum of strong MHD-fluctuations (see e.g. Blandford & Eichler 1987, Bell 2004, Vladimirov et al. 2006). These MHD-fluctuations could carry a substantial fraction of the shock ram pressure to the upstream andthen to the downstream providing a heating source throughout the downstream. The velocity fluctuations could also produce non-thermal broadening of the lines. The amplitude of bulk velocity fluctuations is about the Alfvén velocity since B ~ B in the shock precursor. The Doppler parameter b derived from high resolution UV spectra of the WHIM (see e.g. Lehner et al. 2007e, Richter et al. 2008 - Chapter 3, this volume):

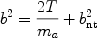would have in the micro-turbulent limit a non-thermal contribution

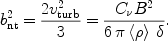The factor C here accounts for the amplitude and spectral shape of the turbulence. For a strong MHD-turbulence that was found in the recent models of strong collisionless shocks with efficient particle acceleration (e.g. Vladimirov et al. 2006) one can get C ~ 1 in the WHIM, and then

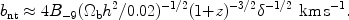The estimation of b_nt given above for a strong Alfvén turbulence may be regarded as an upper limit for a system with a modest MHD turbulence. The non-thermal Doppler parameter does not depend on the ion mass, but b_nt ^-1/2 B(z). Thus the account of b_nt could be important for high resolution spectroscopy of metal lines, especially if the strong shocks can indeed highly amplify local magnetic fields. That is still to be confirmed, but a recent high resolution observation of a strong Balmer-dominated shock on the eastern side of Tycho's supernova remnant with the Subaru Telescope supports the existence of a cosmic ray shock precursor where gas is heated and accelerated ahead of the shock (Lee et al. 2007). High resolution UV spectroscopy of the WHIM could allow to constrain the intergalactic magnetic field. Internal shocks in hot X-ray clusters of galaxies have modest Mach numbers and the effect of the Alfvén turbulence is likely less prominent than that in the strong accretion shocks in clusters and in the cosmic web filaments. X-ray line broadening by large scale bulk motions in the hot intracluster medium was discussed in detail by Fox & Loeb (1997) and Inogamov & Sunyaev (2003).