As stressed above, the presence of diffuse and extended synchrotron emission in galaxy clusters indicates the existence of weak magnetic fields in the cluster volume. Different possibilities for their origin have been proposed which are reviewed by Dolag et al. (2008) - Chapter 15, this volume. Radio observations of galaxy clusters allow us to measure intracluster magnetic fields and test the different theories on their origin, as reviewed by Carilli & Taylor (2002) and Govoni & Feretti (2004). In the following the main methods to study magnetic field intensity and, eventually, structure are summarised.
4.1. Equipartition magnetic fields
In the optically thin case, the total monochromatic emissivity
J(
) from a set of
relativistic electrons in a magnetic field
B depends on a) the magnetic field strength, b)
the energy distribution of the electrons, which is usually assumed to
be a power law (Eq. 1), and c) the pitch angle between the
electron velocity and the magnetic field direction
(
)
 |
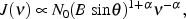(3) |
where 
=
(
- 1) / 2 is the
spectral index of the
synchrotron spectrum 4.
Synchrotron emission from diffuse and extended radio sources can give us a direct measure for the intensity of cluster magnetic fields if the relativistic electron flux is measured or constrained. That can be achieved, for example, if Compton-produced X-ray (and gamma-ray) emission was detected simultaneously (see Sect. 4.2). In the case of polarised radio emission, we can also get an indication of the projected magnetic field orientation and its degree of ordering. To break the degeneracy between magnetic field strength and electron density (Eq. 3), and to obtain a measure for cluster magnetic fields from the observed luminosity of radio sources, it is typically assumed that the energy density of the relativistic plasma within a radio source is minimum
 |
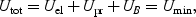(4) |
where UB is the energy density in magnetic fields, and Uel and Upr are the energy in electrons and in protons respectively. The energy in the heavy particles (protons) is considered to be related to the electron energy
 |
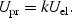(5) |
The value of k depends on the mechanism of
(re-)acceleration of electrons, whose physical details, as seen above,
are still unknown. A typical value of k = 1 is adopted for halo and
relic sources. Another important assumption of this method relates to
the value of the filling factor,
, i.e. the fraction of the
source volume V occupied by magnetic field and relativistic
particles. The energy density in magnetic field is given by
 |
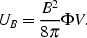(6) |
It is usually considered that particles and magnetic fields
occupy the entire volume, i.e.
= 1. It can be derived
easily that the condition of minimum energy is obtained when the
contributions of cosmic rays and magnetic fields is approximately equal
 |
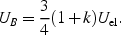(7) |
This is the so-called classical equipartition assumption, which allows us to estimate the magnetic field of a radio source from its radio luminosity L (see Pacholczyk 1970 for a rigorous derivation)
 |
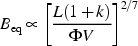(8) |
In the standard approach presented above, L is the
observed synchrotron luminosity between two fixed frequencies
1
and 2 (usually
1 = 10 MHz and
2 = 100 GHz). In
this way, however, the integration limits are variable in terms of the
energy of the radiating electrons, since, based on Eq. 3, electron
energies corresponding to
1 and
2 depend on
magnetic field
values. This point is particularly relevant for the lower limit, owing
to the power-law shape of the electron energy distribution and to the
expected presence of low energy electrons in radio
halos/relics. Alternatively, it has been suggested to derive
equipartition quantities by integrating the electron luminosity over
an energy range (
min -
max)
(Brunetti et
al. 1997,
Beck & Krause
2005).
It can be shown that, for min << max
and > 0.5, the new
expression for the equipartition magnetic field is
 |
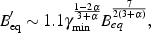(9) |
where Beq is the equipartition magnetic field expressed
in Gauss derived through Eq. 8. Typically, for Beq ~
µG, min ~ 100 and ~ 0.75 - 1, this new
approach gives magnetic field values 2 to 5 times larger than the
standard method.
Estimates of equipartition fields on scales as large as ~1 Mpc
give magnetic field intensities in the range 0.1-1 µG. As we
have seen, these estimates are based on several assumptions both on
different physical properties of the radio emitting region (e.g. the
filling factor and the
ratio between electron and proton
energies k), and on the condition of minimum energy of the observed
relativistic plasma. Since the validity of these assumptions is not
obvious, one has to be aware of the uncertainties and thus of the
limits inherent to the equipartition determination of magnetic fields.
4.2. Compton scattering of CMB photons
As reviewed by Rephaeli et al. (2008) - Chapter 5, this volume, 3K microwave background photons can be subject to Compton scattering by electrons in the cluster volume. If the presence of thermal particles in the ICM results in a distortion of the Cosmic Microwave Background (CMB) spectrum well known as "Sunyaev-Zel'dovich effect" (Sunyaev & Zel'dovich 1972), non-thermal hard X-ray (HXR) photons are produced via Compton scattering by the same cosmic rays that are responsible for the synchrotron emission observed at radio wavelengths. Compton scattering increases the frequency of the incoming photon through
 |
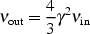(10) |
The Planck function of the CMB peaks at
in ~
1.6 × 1011 Hz. Based on Eq. 10, for typical energies
of relativistic electrons in clusters
( ~ 1000
- 5000), the scattered photons fall in the X-ray and gamma-ray domain (~
2 × 1017 - 5×1018 Hz, i.e. ~ 0.8 - 20.7
keV).
Non-thermal HXR emission from galaxy clusters due to Compton scattering of CMB photons was predicted more than 30 years ago (e.g. Rephaeli 1977) and has now been detected in several systems (Rephaeli et al. 2008 - Chapter 5, this volume; Fusco-Femiano et al. 2007 and references therein). Alternative interpretations to explain the detected non-thermal X-ray emission have been proposed in the literature (Blasi & Colafrancesco 1999, Enßlin et al. 1999, Blasi 2000, Dogiel 2000, Sarazin & Kempner 2000). However, these hypotheses seem to be ruled out by energetic considerations, because of the well known inefficiency of the proposed non-thermal Bremsstrahlung (NTB) mechanism. NTB emission of keV regime photons with some power P immediately imply about 105 times larger power to be dissipated in the plasma that seems to be unrealistic in a quasi-steady model (Petrosian 2001, 2003). For a more detailed treatment of the origin of HXR emission from galaxy clusters, see the review by Petrosian et al. (2008) - Chapter 10, this volume.
The detection of non-thermal HXR and radio emission, produced by the
same population of relativistic electrons, allows us to estimate
unambiguously the volume-averaged intracluster magnetic
field. Following the exact derivations by
Blumenthal
& Gould (1970),
the equations for the synchrotron flux fsyn at the
frequency R
and the Compton X-ray flux fC at the frequency
X are
 |
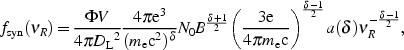(11) |
 |
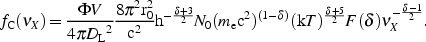(12) |
Here h is the Planck constant, V is the volume of the
source and the filling
factor, DL is the luminosity distance
of the source, B the magnetic field strength, T the radiation
temperature of the CMB, r0 the classical electron
radius (or Thomson scattering length), N0 and
are the amplitude and
the spectral index of the electron energy distribution
(Eq. 1). The values of the functions
a() and
F() for different
values of can be found
in
Blumenthal
& Gould (1970).
The field B can thus be estimated directly from these equations
 |
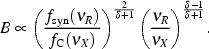(13) |
Typical cluster magnetic field values of ~ 0.1 - 0.3 µG are obtained (e.g. Rephaeli et al. 1999, Fusco-Femiano et al. 1999, Fusco-Femiano et al. 2000, Fusco-Femiano et al. 2001, Rephaeli & Gruber 2003, Rephaeli et al. 2006). Compared to equipartition measures, this method has the great advantage of using only observables, assuming only that the spatial factors in the expressions for the synchrotron and Compton fluxes (Rephaeli 1979) are identical.
Faraday rotation analysis of radio sources in the background or in the galaxy clusters themselves is one of the key techniques used to obtain information on the cluster magnetic fields. The presence of a magnetised plasma between an observer and a radio source changes the properties of the polarised emission from the radio source. Therefore information on cluster magnetic fields along the line-of-sight can be determined, in conjunction with X-ray observations of the hot gas, through the analysis of the Rotation Measure (RM) of radio sources (e.g. Burn 1966).
The polarised synchrotron radiation coming from radio galaxies undergoes the following rotation of the plane of polarisation as it passes through the magnetised and ionised intracluster medium
 |
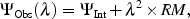(14) |
where 
Int is
the intrinsic polarisation angle, and
Obs(
) is the polarisation angle
observed at a wavelength
. The RM is related to
the thermal electron
density (ne), the magnetic field along the line-of-sight
(B||), and the path-length (L) through the
intracluster medium according to
 |
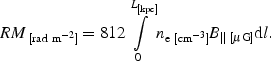(15) |
Polarised radio galaxies can be mapped at several frequencies to produce, by fitting Eq. 14, detailed RM images. Once the contribution of our Galaxy is subtracted, the RM should be dominated by the contribution of the intracluster medium, and therefore it can be used to estimate the cluster magnetic field strength along the line of sight.
The RM observed in radio galaxies may not be all due to the cluster magnetic field if the RM gets locally enhanced by the intracluster medium compression due to the motion of the radio galaxy itself. However a statistical RM investigation of point sources (Clarke et al. 2001, Clarke 2004) shows a clear broadening of the RM distribution toward small projected distances from the cluster centre, indicating that most of the RM contribution comes from the intracluster medium. This study included background sources, which showed similar enhancements as the embedded sources.
We also note that there are inherent uncertainties in the determination of field values from Faraday Rotation measurements, stemming largely from the unknown small-scale tangled morphology of intracluster fields, their large-scale spatial variation across the cluster, and from the uncertainty in modelling the gas density profile (see e.g., Goldshmidt & Rephaeli 1993, Newman et al. 2002, Rudnick & Blundell 2003a, Enßlin et al. 2003, Murgia et al. 2004).
RM studies of radio galaxies have been carried out on both statistical samples (e.g. Lawler & Dennison 1982, Vallee et al. 1986, Kim et al. 1990, Kim et al. 1991, Clarke et al. 2001) and individual clusters by analysing detailed high resolution RM images (e.g. Perley & Taylor 1991, Taylor & Perley 1993, Feretti et al. 1995, Feretti et al. 1999, Govoni et al. 2001a, Taylor et al. 2001, Eilek & Owen 2002, Govoni et al. 2006, Taylor et al. 2007, Guidetti et al. 2007). Both for interacting and relaxed (cooling flow) clusters the RM distribution of radio galaxies is generally patchy, indicating that cluster magnetic fields have structures on scales as low as 10 kpc or less. RM data are usually consistent with central magnetic field strengths of a few µG. But, radio galaxies at the centre of relaxed clusters have extreme RM, with the magnitude of the RM roughly proportional to the cooling flow rate (see Fig. 6). Strong magnetic fields are derived in the high density cooling-core regions of some clusters, with values exceeding ~ 10 µG (e.g., in the inner region of Hydra A, a value of ~ 35 µG was deduced by Taylor et al. 2002). It should be emphasised that such high field values are clearly not representative of the mean fields in large extended regions.
 |
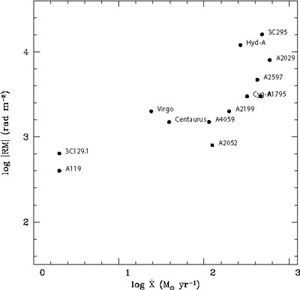Figure 6. RM magnitudes of a sample of radio galaxies located in cooling flow clusters, plotted as a function of the cooling flow rate X (from [Taylor et al. 2002]). |
Dolag et al. (2001b) showed that, in the framework of hierarchical cluster formation, the correlation between two observable parameters, the RM and the cluster X-ray surface brightness in the source location, is expected to reflect a correlation between the cluster magnetic field and gas density. Therefore, from the analysis of the RM versus X-ray brightness it is possible to infer the trend of magnetic field versus gas density.
On the basis of the available high quality RM images, increasing attention is given to the power spectrum of the intracluster magnetic field fluctuations. Several studies (Enßlin & Vogt 2003, Murgia et al. 2004) have shown that detailed RM images of radio galaxies can be used to infer not only the cluster magnetic field strength, but also the cluster magnetic field power spectrum. The analyses of Vogt & Enßlin (2003, 2005) and Guidetti et al. (2007) suggest that the power spectrum is of the Kolmogorov type, if the auto-correlation length of the magnetic fluctuations is of the order of few kpc. However, Murgia et al. (2004) and Govoni et al. (2006) pointed out that shallower magnetic field power spectra are possible if the magnetic field fluctuations extend out to several tens of kpc.
4.4. Comparison of the different methods
As shown in Table 3 of Govoni & Feretti (2004), the different methods available to measure intracluster magnetic fields show quite discrepant results (even more than a factor 10). RM estimates are about an order of magnitude higher than the measures derived both from the synchrotron diffuse radio emission and the non-thermal hard X-ray emission (~ 1 - 5 µG vs. ~ 0.2 - 1 µG).
This can be due to several factors. Firstly, equipartition values are severely affected by the already mentioned physical assumptions of this method. Secondly, while RM estimates give a weighted average of the field along the line of sight, equipartition and Compton scattering measures are made by averaging over larger volumes. Additionally, discrepancies can be due to spatial profiles of both the magnetic field and the gas density not being constant all over the cluster (Goldshmidt & Rephaeli 1993), or due to compressions, fluctuations and inhomogeneities in the gas and in the magnetic field, related to the presence of radio galaxies or to the dynamical history of the cluster (e.g. on-going merging events) (Beck et al. 2003, Rudnick & Blundell 2003b, Johnston-Hollitt 2004). Finally, a proper modelling of the Compton scattering method should include a) the effects of aged electron spectra, b) the expected radial profile of the magnetic field, and c) possible anisotropies in the pitch angle distribution of electrons (Brunetti et al. 2001, Petrosian 2001).
An additional method of estimating cluster magnetic fields comes from
the X-ray analysis of cold fronts
(Vikhlinin et
al. 2001).
These X-ray cluster features, discovered by
Markevitch et
al. (2000)
thanks to the exquisite spatial resolution of the Chandra
satellite, result
from dense cool gas moving with near-sonic velocities through the less
dense and hotter ICM. Cold fronts are thus subject to Kelvin-Helmholtz
(K-H) instability that, for typical cluster and cold front properties
(Mach number, gas temperatures, cluster-scale length), could quickly
disturb the front outside a narrow
(
10°) sector in
the direction of the cool cloud motion
5.
Through the Chandra observation of A 3667,
Vikhlinin et
al. (2001)
instead revealed a cold front that is stable within a ± 30°
sector. They showed that a ~ 10 µG magnetic field oriented
nearly parallel to the front is able
to suppress K-H instability, thus preserving the front structure, in a
± 30° sector. The estimated magnetic field value,
significantly higher than the typical measures given by the other
methods outside cluster cooling flows, is likely an upper limit of the
absolute field strength. Near the cold front the field is actually
amplified by tangential gas motions (see
Vikhlinin et
al. 2001).
Variations of the magnetic field structure and strength with the cluster radius have been recently pointed out by Govoni et al. (2006). By combining detailed multi-wavelength and numerical studies we will get more insight into the strength and structure of intracluster magnetic fields, and into their connection with the thermodynamical evolution of galaxy clusters. More detailed comparisons of the different approaches for measuring intracluster magnetic fields can be found, for instance, in Petrosian (2003) and Govoni & Feretti (2004).
4
is the electron energy
index, see Eq. 1.
Back.
5 For a more precise treatment, see Vikhlinin et al. (2001) and Markevitch & Vikhlinin (2007). Back.