


The electrons in an atom have orbits with discrete energy levels and quantum numbers. The principal quantum number n corresponds to the energy In of the orbit (in the classical Bohr model for the hydrogen atom the energy In = EH n-2 with EH = 13.6 eV the Rydberg energy), and it takes discrete values n = 1, 2, 3, …. An atomic shell consists of all electrons with the same value of n.
The second quantum number  corresponds to the angular momentum of the electron, and takes discrete
values
corresponds to the angular momentum of the electron, and takes discrete
values  < n. Orbits
with
< n. Orbits
with  = 0, 1, 2, 3 are
designated as s, p, d, and f orbits. A subshell
consists of all electrons with the same value of n and
= 0, 1, 2, 3 are
designated as s, p, d, and f orbits. A subshell
consists of all electrons with the same value of n and
 ;
they are usually designated as 1s, 2s, 2p, etc.
;
they are usually designated as 1s, 2s, 2p, etc.
The spin quantum number s of an electron can take values s
= ± 1/2, and the combined total angular momentum j has a
quantum number with values between
 - 1/2 (for
- 1/2 (for
 > 0) and
> 0) and
 + 1/2. Subshells are
subdivided according to their j-value and are designated as
n
+ 1/2. Subshells are
subdivided according to their j-value and are designated as
n  j.
Example: n = 2,
j.
Example: n = 2,
 = 1,
j = 3/2 is designated as 2p3/2.
= 1,
j = 3/2 is designated as 2p3/2.
There is also another notation that is commonly used in X-ray spectroscopy.
Shells with n = 1, 2, 3, 4, 5, 6 and 7 are indicated with K, L,
M, N, O, P, Q. A further subdivision is made starting from low values of
 up to higher
values of
up to higher
values of  and from low
values of j up to higher values of j:
and from low
values of j up to higher values of j:
| 1s | 2s | 2p1/2 | 2p3/2 | 3s | 3p1/2 | 3p3/2 | 3d3/2 | 3d5/2 | 4s | etc. |
| K | LI | LII | LIII | MI | MII | MIII | MIV | Mv | NI | |
| 2 | 2 | 2 | 4 | 2 | 2 | 4 | 4 | 6 | 2 |
The third row in this table indicates the maximum number of electrons that can be contained in each subshell. This so-called statistical weight is simply 2j + 1.
Atoms or ions with multiple electrons in most cases have their shells filled
starting from low to high n and
 . For example, neutral
oxygen has 8 electrons, and the shells are filled like
1s22s22p4, where the
superscripts denote the number of electrons in each shell. Ions or atoms
with completely filled subshells (combining all allowed j-values)
are particularly stable. Examples are the noble gases: neutral helium,
neon and argon, and more general all ions with 2, 10 or 18 electrons. In
chemistry, it is common practice to designate ions by the number of
electrons that they have lost, like O2+
for doubly ionised oxygen. In astronomical spectroscopic practice, more
often one starts to count with the neutral atom, such that
O2+ is designated as O III. As the atomic structure and the
possible transitions of an ion
depend primarily on the number of electrons it has, there are all kinds of
scaling relationships along so-called iso-electronic sequences. All ions
on an iso-electronic sequence have the same number of electrons; they
differ only by the nuclear charge Z. Along such a sequence,
energies, transitions or rates are often continuous functions of
Z. A well known example is the famous
1s-2p triplet of lines in the helium iso-electronic sequence (2-electron
systems), e.g. C V, N VI and O VII.
. For example, neutral
oxygen has 8 electrons, and the shells are filled like
1s22s22p4, where the
superscripts denote the number of electrons in each shell. Ions or atoms
with completely filled subshells (combining all allowed j-values)
are particularly stable. Examples are the noble gases: neutral helium,
neon and argon, and more general all ions with 2, 10 or 18 electrons. In
chemistry, it is common practice to designate ions by the number of
electrons that they have lost, like O2+
for doubly ionised oxygen. In astronomical spectroscopic practice, more
often one starts to count with the neutral atom, such that
O2+ is designated as O III. As the atomic structure and the
possible transitions of an ion
depend primarily on the number of electrons it has, there are all kinds of
scaling relationships along so-called iso-electronic sequences. All ions
on an iso-electronic sequence have the same number of electrons; they
differ only by the nuclear charge Z. Along such a sequence,
energies, transitions or rates are often continuous functions of
Z. A well known example is the famous
1s-2p triplet of lines in the helium iso-electronic sequence (2-electron
systems), e.g. C V, N VI and O VII.
2.2. Level notation in multi-electron systems
For ions or atoms with more than one electron, the atomic structure is
determined by the combined quantum numbers of the electrons. These quantum
numbers have to be added according to the rules of quantum mechanics. We
will not go into detail here, but refer to textbooks such as
Herzberg
(1944).
The determination of the allowed quantum states and the transitions between
these states can be rather complicated. Important here is to know that
for each electron configuration (for example 1s 2p) there is a number of
allowed terms or multiplets, designated as 2S+1L, with
S the combined electron spin
(derived from the individual s values of the electrons), and
L represents the combined angular momentum (from the individual
 values). For L one
usually substitutes the alphabetic designations similar to those for single
electrons, namely S for L = 0, P for L = 1, etc. The
quantity 2S + 1 represents the multiplicity of the term, and
gives the number of distinct energy levels of
the term. The energy levels of each term can be distinguished by
J, the combined total angular momentum quantum number j of
the electrons. Terms with
2S + 1 equals 1, 2 or 3 are designated as singlets, doublets and
triplets, etc.
values). For L one
usually substitutes the alphabetic designations similar to those for single
electrons, namely S for L = 0, P for L = 1, etc. The
quantity 2S + 1 represents the multiplicity of the term, and
gives the number of distinct energy levels of
the term. The energy levels of each term can be distinguished by
J, the combined total angular momentum quantum number j of
the electrons. Terms with
2S + 1 equals 1, 2 or 3 are designated as singlets, doublets and
triplets, etc.
For example, a configuration with two equivalent p electrons (e.g., 3p2), has three allowed terms, namely 1S, 1D and 3P. The triplet term 3P has 2S + 1 = 3 hence S = 1 and L = 1 (corresponding to P), and the energy levels of this triplet are designated as 3P0, 3P1 and 3P2 according to their J values 0, 1 and 2.
The binding energy I of K-shell electrons in neutral atoms increases approximately as I ~ Z2 with Z being the nuclear charge (see Table 1 and Fig. 1). Also for other shells the energy increases strongly with increasing nuclear charge Z.
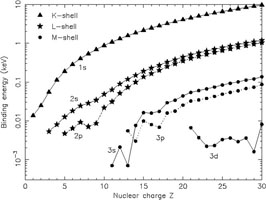 |
Figure 1. Energy levels of atomic subshells for neutral atoms. |
| Z | E |  |
 |
Z | E |  |
 |
|||
| (eV) | (Å) | (Mbarn) | (eV) | (Å) | (Mbarn) | |||||
| 1s shell: | 2s shell: | |||||||||
| H | 1 | 13.6 | 911.8 | 6.29 | O | 8 | 16.6 | 747.3 | 1.37 | |
| He | 2 | 24.6 | 504.3 | 7.58 | Si | 14 | 154 | 80.51 | 0.48 | |
| C | 6 | 288 | 43.05 | 0.96 | S | 16 | 232 | 53.44 | 0.37 | |
| N | 7 | 403 | 30.77 | 0.67 | Ar | 18 | 327 | 37.97 | 0.29 | |
| O | 8 | 538 | 23.05 | 0.50 | Ca | 20 | 441 | 28.11 | 0.25 | |
| Ne | 10 | 870 | 14.25 | 0.29 | Fe | 26 | 851 | 14.57 | 0.15 | |
| Mg | 12 | 1308 | 9.48 | 0.20 | Ni | 28 | 1015 | 12.22 | 0.13 | |
| Si | 14 | 1844 | 6.72 | 0.14 | 2p1/2 shell: | |||||
| S | 16 | 2476 | 5.01 | 0.096 | S | 16 | 169 | 73.26 | 1.61 | |
| Ar | 18 | 3206 | 3.87 | 0.070 | Ar | 18 | 251 | 49.46 | 1.45 | |
| Ca | 20 | 4041 | 3.07 | 0.060 | Ca | 20 | 353 | 35.16 | 0.86 | |
| Fe | 26 | 7117 | 1.74 | 0.034 | Fe | 26 | 726 | 17.08 | 0.42 | |
| Ni | 28 | 8338 | 1.49 | 0.029 | Ni | 28 | 877 | 14.13 | 0.35 | |
| 2p3/2 shell: | ||||||||||
| S | 16 | 168 | 73.80 | 3.24 | ||||||
| Ar | 18 | 249 | 49.87 | 2.97 | ||||||
| Ca | 20 | 349 | 35.53 | 1.74 | ||||||
| Fe | 26 | 713 | 17.39 | 0.86 | ||||||
| Ni | 28 | 860 | 14.42 | 0.73 | ||||||
For ions of a given element the ionisation energies decrease with decreasing ionisation stage: for lowly ionised ions, a part of the Coulomb force exerted on an electron by the positively charged nucleus is compensated by the other electrons in the ion, thereby allowing a wider orbit with less energy. An example is given in Table 2.
| Ion | E |  |
 |
| (eV) | (Å) | (Mbarn) | |
| (10-22 m2) | |||
| O I | 544 | 22.77 | 0.50 |
| O II | 565 | 21.94 | 0.45 |
| O III | 592 | 20.94 | 0.41 |
| O IV | 618 | 20.06 | 0.38 |
| O V | 645 | 19.22 | 0.35 |
| O VI | 671 | 18.48 | 0.32 |
| O VII | 739 | 16.77 | 0.24 |
| O VIII | 871 | 14.23 | 0.10 |
With high spectral resolution and sensitivity, optical spectra of stars sometimes show spectral features from almost all elements of the Periodic Table, but in practice only a few of the most abundant elements show up in X-ray spectra of cosmic plasmas. In several situations the abundances of the chemical elements in an X-ray source are similar to (but not necessarily equal to) the abundances for the Sun or a constant fraction of that. There have been many significant changes over the last several years in the adopted set of standard cosmic abundances. A still often used set of abundances is that of Anders & Grevesse (1989), but a more recent one is the set of proto-solar abundances of Lodders (2003), that we list in Table 3 for a few of the key elements.
| Element | abundance | Element | abundance | Element | abundance | ||
| H |  1
1 |
Ne | 89.1 × 10-6 | S | 18.2 × 10-6 | ||
| He | 0.0954 | Na | 2.34 × 10-6 | Ar | 4.17 × 10-6 | ||
| C | 288 × 10-6 | Mg | 41.7 × 10-6 | Ca | 2.57 × 10-6 | ||
| N | 79.4 × 10-6 | Al | 3.47 × 10-6 | Fe | 34.7 × 10-6 | ||
| O | 575 × 10-6 | Si | 40.7 × 10-6 | Ni | 1.95 × 10-6 | ||
In general, for absorption studies the strength of the lines is mainly determined by atomic parameters that do not vary much along an iso-electronic sequence, and the abundance of the element. Therefore, in the X-ray band the oxygen lines are the strongest absorption lines, as oxygen is the most abundant metal. The emissivity of ions in the X-ray band often increases with a strong power of the nuclear charge. For that reason, in many X-ray plasmas the strongest iron lines are often of similar strength to the strongest oxygen lines, despite the fact that the cosmic abundance of iron is only 6% of the cosmic oxygen abundance.