8. COOLING FUNCTION

The cooling of a plasma by thermal radiation is usually expressed by the cooling function (T). This is essentially the bolometric power P emitted as thermal radiation by the plasma, normalised by the emission measure Y = n_e n_H V. Accordingly, the characteristic cooling time, defined as the thermal energy of the plasma divided by the emitted power, t_cool = 3/2 (1 + n_i / n_e) k T / n_H.

Cooling is important for the evolution of several plasmas such as the cool cores of clusters but also for the global evolution of the WHIM. A set of useful cooling curves are given by Sutherland & Dopita (1993). An example is shown in Fig. 15. These are valid under CIE conditions. When photoionisation is important, modifications are needed. Here we have normalised to the emission measure of the plasma, but note that sometimes other scalings are being used (for example expressions containing the ion density n_i or n_e²). Note that the Solar abundances used in Fig. 15 are the older values of Anders & Grevesse (1989) which differ significantly from more recent estimates, for example Lodders (2003), in particular for important coolants such as iron (new values 26% lower) and oxygen (new values 32% lower). The big hump at low temperatures is produced mainly by line radiation, while the high temperature ~ T^0.5 tail above 10⁷ K is mainly produced by Bremsstrahlung.

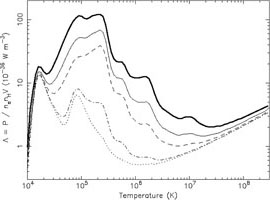Figure 15. Cooling curves (T) for plasmas of different composition, under CIE conditions. From top to bottom: 1, 0.3, 0.1, 0.01 and 0.001 times solar abundances. After Sutherland & Dopita (1993).

Finally, a more recent set of cooling curves, suited in particular for lower temperatures and primordial gas, was published by Maio et al. (2007).