6. MATTER-ENERGY CONTENT OF THE UNIVERSE

6.1. Dark Matter and Dark Energy

In early papers on dark matter the total density due to visible and dark matter was estimated to be about 0.2 of the critical cosmological density. These estimates were based on the dynamics of galaxies in groups and clusters. This density estimate can be interpreted in two different ways: either we live in an open Universe where the total density is less than the critical density, or there exists some additional form of matter/energy which allows the Universe to be closed, i.e. to have the critical total density. The additional term was identified with the Einstein -term, so that the total matter/energy density was taken to be equal to the critical cosmological density (Gunn & Tinsley 1975, Turner et al. 1984, Kofman & Starobinskii 1985). Initially there was no direct observational evidence in favour of this solution and it was supported basically on general theoretical grounds. In its early evolution the size of the Universe increases very rapidly and any deviation from the exact critical density would lead to a rapid change of the relative density, either to zero, if the initial density was a bit less than the critical one, or to infinity, if it was greater than critical. In other words, some fine tuning is needed to keep the density at all times equal to the critical one.

In subsequent years several new independent methods were applied to estimate the cosmological parameters. Of these new methods two desire special attention. One of them is based on the measurements of small fluctuations of the Cosmic Microwave Background (CMB) radiation, and the other on the observation of distant supernovae.

According to the present cosmological paradigm the Universe was initially very hot and ionized. The photons provided high pressure and prevented baryons from moving. Perturbations of baryons did not grow, but oscillated as sound waves. The largest possible wavelength of these oscillations is given by the sound horizon size at the decoupling. This wavelength is seen as the first maximum in the angular power spectrum of the CMB radiation. The following maxima correspond to overtones of the first one. The fluctuations of CMB radiation were first detected by the COBE satellite. The first CMB data were not very accurate, since fluctuations are very small, of the order of 10^-5. Subsequent experiments carried out using balloons, ground based instruments, and more recently the Wilkinson Microwave Anisotropy Probe (WMAP) satellite, allowed to measure the CMB radiation and its power spectrum with a much higher precision (Spergel et al. 2003). The position of the first maximum of the power spectrum depends on the total matter/energy density. Observations confirm the theoretically favoured value 1 in units of the critical cosmological density, see Fig. 15.

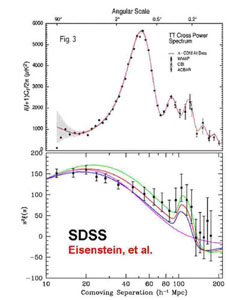Figure 15. Upper panel shows the acoustic peaks in the angular power spectrum of the CMB radiation according to the WMAP and other recent data, compared with the CDM model using all available data. The lower panel shows the signature of baryonic acoustic oscillations in the matter two-point correlation function (Eisenstein et al. 2005, Kolb 2007) (reproduced by permission of the author).

When recombination begins, the small overdensities of baryon gas launch spherical shock waves in the photon-baryon fluid. After some time photons completely decouple from baryons, and the baryons loose photon pressure support. The shock stops after traveling a distance of about 150 Mpc (in comoving coordinates). This leads to an overdensity of the baryonic medium on a distance scale of 150 Mpc. This overdensity has been recently detected in the correlation function of Luminous Red Giant galaxies of the SDSS survey (Eisenstein et al. 2005, Hütsi 2006), see lower panel of Fig. 15. Baryonic acoustic oscillations depend on both the total matter/energy density and the baryon density, thus allowing to estimate these parameters.

Another independent source of information on cosmological parameters comes from the distant supernova experiments. Two teams, led by Riess et al. (1998, 2007) (High-Z Supernova Search Team) and Perlmutter et al. (1999) (Supernova Cosmology Project), initiated programs to detect distant type Ia supernovae in the early stage of their evolution, and to investigate with large telescopes their properties. These supernovae have an almost constant intrinsic brightness (depending slightly on their evolution). By comparing the luminosities and redshifts of nearby and distant supernovae it is possible to calculate how fast the Universe was expanding at different times. The supernova observations give strong support to the cosmological model with the term, see Fig. 16.

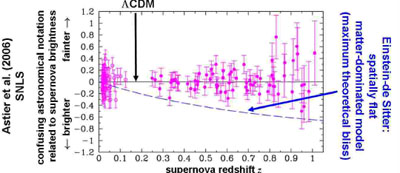Figure 16. Results of the Supernova Legacy Survey: apparent magnitudes of supernovae are normalised to the standard CDM model, shown as solid line. Dashed line shows the Einstein-de Sitter model with m = 1 (Kolb 2007) (reproduced by permission of the author).

Different types of dark energy affect the rate at which the Universe expands, depending on their effective equation of state. The cosmological constant has one equation of state. The other possible candidate of dark energy is quintessence (a scalar field) that has a different equation of state. Each variant of dark energy has its own equation of state that produces a signature in the Hubble diagram of the type Ia supernovae (Turner 2003).

The combination of the CMB and supernova data allows to estimate independently the matter density and the density due to dark energy, shown in Fig. 17. The results of this combined approach imply that the Universe is expanding at an accelerating rate. The acceleration is due to the existence of some previously unknown dark energy (or cosmological constant) which acts as a repulsive force (for reviews see Bahcall et al. 1999, Frieman et al. 2008).

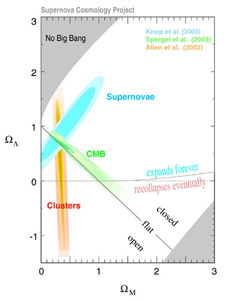Figure 17. Combined constraints to cosmological densities and m, using supernovae, CMB and cluster abundance data. The flat Universe with + m = 1 is shown with solid line (Knop et al. 2003).

Independently, the matter density parameter has been determined from clustering of galaxies in the 2-degree Field Redshift Survey and the Sloan Digital Sky Survey. The most accurate estimates of cosmological parameters are obtained using a combined analysis of the 2dFGRS, SDSS and the WMAP data (Spergel et al. 2003, Tegmark et al. 2004, Sánchez et al. 2006). According to these studies the matter density parameter is _m = 0.27 ± 0.02, not far from the value _m = 0.3, suggested by Ostriker & Steinhardt (1995) as a concordant model. The combined method yields for the Hubble constant a value h = 0.71 ± 0.02 independent of other direct methods. From the same dataset authors get for the density of baryonic matter, _b = 0.041 ± 0.002. Comparing both density estimates we get for the dark matter density _DM = _m - _b = 0.23, and the dark energy density = 0.73. These parameters imply that the age of the Universe is 13.7 ± 0.2 Gigayears.

6.2. The role of dark energy in the evolution of the Universe

Studies of the Hubble flow in nearby space, using observations of type Ia supernovae with the Hubble Space Telescope (HST), were carried out by several groups. The major goal of the study was to determine the value of the Hubble constant. As a by-product also the smoothness of the Hubble flow was investigated. In this project supernovae were found up to the redshift (expansion speed) 20000 km s^-1. This project (Sandage et al. 2006) confirmed earlier results that the Hubble flow is very quiet over a range of scales from our Local Supercluster to the most distant objects observed. This smoothness in spite of the inhomogeneous local mass distribution requires a special agent. Vacuum energy as the solution has been proposed by several authors (Baryshev et al. 2001 and others). Sandage emphasises that no viable alternative to vacuum energy is known at present, thus the quietness of the Hubble flow gives strong support for the existence of vacuum energy.