9. COMPARISON OF STAR FORMATION MODELS

Choi & Nagamine (2010) compared three models for star formation in cosmological simulations, the Springel & Hernquist (2003) model, the Blitz & Rosolowsky (2006) model, and the Schaye & Dalla Vecchia (2008) model. These are instructive to review here so that the diversity of analytical models can be noted.

In the Springel & Hernquist (2003) model, there is cooling gas with a star formation rate

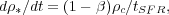(9.1)

where equals the supernova gas return fraction, _c equals the density of cool clouds, t_SFR = t₀^*( / _th)^-1/2 is the dynamical time, where t₀^* = 2.1 Gyr gives the local KS law. They also assumed _SFR = 0 if < _th for threshold column density _th, and _SFR = A(_gas / 1 M pc²)ⁿ for A = 2.5 ± 0.7 M yr^-1 kpc^-2, n = 1.4, and _th = 10 M pc^-2. This equation for star formation rate is combined with another equation for the rate of change of the cool cloud density,

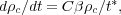(9.2)

where C = C₀( / _th)^-4/5. This assumes that supernovae evaporate and form cold clouds as in McKee & Ostriker (1977).

In the Blitz & Rosolowsky (2006) model, the molecular fraction is given by _H2 / _HI = (P_ext / P₀)^0.92, where P₀ = 4.3 × 10⁴ k_B K cm^-3. Then for a star formation rate, they assume

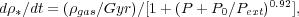(9.3)

which assumes (a constant scale height). This star formation rate was applied only when P_ext < P₀. For P_ext > P₀, Choi & Nagamine (2010) used the Springel & Hernquist law (i.e., the Kennicutt n = 1.4 law).

The third model was that of Schaye & Dalla Vecchia (2008). These authors solved for the scale height using _gas = _gas L_Jeans = ( f_g P_tot / G)^1/2, where is the adiabatic index: P_tot ~ _gas (P_tot and _tot include stars), f_g equals the gas mass fraction, and f_th equals the thermal pressure fraction (P = f_th P_tot). They assumed f_g = f_th, so if _SFR = A _gasⁿ = _gas / t which means t = _gas^1-n / A, then t_SFR = A^-1(M pc²)ⁿ( P / G)^(1-n)/2, and finally d_* / dt = _gas / t_SFR. Note that in this model, _{SFR gas} P^0.2. They also assumed a threshold density, _th = _th / L_Jeans, so _th = _th² G / c_s² f_g for c_s = 1.8 km s^-1 (500K gas), and they assumed P = K ^4/3.

Choi & Nagamine (2010) note that the Springel & Hernquist model forms too many stars at low _gas and this causes it to form stars too early in the Universe. The other models have a pressure dependence for star formation which gives an acceptably low rate in low pressure regions.

Genzel et al. (2010) reviewed the star formation and CO data for high-z galaxies in the context of the "main-sequence line" for star formation:

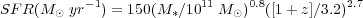(9.4)

(Bouche et al. 2010, Noeske et al. 2007, Daddi et al. 2007).

Genzel et al. noted that the gas depletion time depends weakly on z. It is ~ 0.5 Gyr at z > 1, and 1.7 Gyr at z = 0, while mergers have 2.5-7.5 × shorter depletion times than non-mergers. At z > 1, the depletion time is comparable to the stellar age, and it is always shorter than the Hubble time. This means there is a continuous need for gas replenishment in galaxy disks.

Genzel et al. also found that the molecular star formation-column density relation is in agreement with Bigiel et al. (2008). There is no steepening at _gas > 100 M pc^-2 like there appears to be in local starbursts. In general, they find no variation in the empirical star formation law with redshift.

The dynamical version of the Kennicutt (1998) relation was examined by Genzel et al. too. The dynamical relation says that the star formation rate is proportional to the gas column density divided by the local orbit time. Even in this form, mergers were found to be more efficient at star formation than non-mergers. The star formation efficiency per unit dynamical time was about 1.7%.

These considerations led Genzel et al. to a fundamental plane of star formation, in which the total galactic star formation rate depends only on the dynamical time and the total molecular mass:

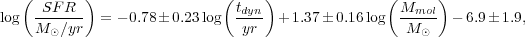(9.5)

all with a standard deviation of 0.47 dex. This is the same as

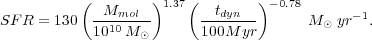(9.6)

Genzel et al. (2010) summarized the various star formation-density laws as follows. The Kennicutt slope of ~ 1.4 includes HI, whereas the Bigiel et al. (2008) slope of ~ 1 is just for CO (or H₂). Genzel et al. redid the Kennicutt (1998) slope of 1.4 with just H₂ and got a slope of ~ 1.33. They redid their own relation for _SFR versus _gas including HI in addition to H₂ and found that it increases the slope from 1.17 to 1.28. Kennicutt (1998) used the same CO-H₂ conversion factor everywhere. When Genzel et al. redid the Kennicutt (1998) data with a variable CO-H₂ conversion factor including only H₂, the slope increased from 1.33 to 1.42. Thus the inclusion of HI and the constant CO-H₂ conversion factor somewhat cancel each other in the Kennicutt (1998) relation. Genzel et al. (2010) also included new merger galaxies, which flatten the slope compared to that in Kennicutt (1998). Writing the star formation rate as _mol / t_dyn works fairly well, including both mergers and normal galaxies at all redshifts.

Daddi et al. (2010b) fitted Ultrahigh Luminosity Infrared Galaxies (ULIRGS) and Submillimeter Wave Galaxies (SMGs) to the same star formation-column density relation if the SF law is _SFR ~ _gas / t_dyn (t_dyn is the rotation time at the outer disk radius). They suggested that the global star formation rate is proportional so ~ (M_{total gas} / t_dyn)^1.42. High SFR galaxies consume their gas faster than a rotation time at the outer radius. This suggests that mergers are involved, or some other rapid accretion leading to centralized star formation.