Expanding shells are most commonly made by stellar pressures in the
form of HII regions, supernovae, and winds. If we write the expansion
speed as dR / dt ~ (P /
)1/2
for an isothermal shock, then the
radius varies as a power law in time if the pressure P is a function
of radius R and the density
is
uniform. For an HII region,
P = 2.1nkT where n = (3S /
4
R3
)1/2 for ionizing
luminosity S in photons per second and recombination rate
to
all but the ground state. Then P
R-3/2. For supernovae, P ~ 3E /
4 R3 for the
energy conserving, non-radiative, phase. For a wind, P ~
3E(t) / 4
R3, where the energy increases with time as
E = Lt.
These three pressure-radius relations give three different radius-time
expansion laws, dR / dt
R-3/4 gives R
t4/7 for a
Strömgren sphere, dR / dt
R-3/2 gives R ~ t2/5 for
the Sedov phase of a supernova, and dR / dt
t1/2R-3/2
gives R
t3/5 for a steady wind or continuous energy supply
from multiple supernovae in an OB association
(Castor et
al. 1975).
There are many complications to these solutions. External pressure is
always present, slowing down the bubbles. External pressure
Pext enters the expression as dR / dt =
([P - Pext] /
)1/2
with Pext ~ constant. The solution is not a power law
in this case. A second complication is the momentum in the moving
shell. When this is important, the equation of expansion is really
d(4
R3 v
/3) /
dt = 4
R2 (P -
Pext). Shell momentum makes the shell
move faster at a given radius than in the case without momentum. There
are also diverse shock jump conditions depending on the importance of
magnetic fields and the equation of state for the shocked gas, such as
adiabatic or isothermal, or whether the full energy equation is used to
determine the post-shock temperature.
We can see how important external pressure is to these solutions by
finding the fraction of shells that are at a pressure significantly
above the external value. As noted above, each source has solutions
R(t) and P(R), which can be re-written into
a solution for pressure versus time, P(t). Thus there is a
relation for the volume as a
function of pressure, V(P). For a constant rate
n0 of making
bubbles, n(P)dP = n0
dt. Therefore n(P)
dt /
dP. The volume filling factor is f(P) =
n(P)V(P). Now we see that for HII regions,
f(P)
P-4.17; for winds, f(P)
P-4.5, and for supernovae, f(P)
P-5.2. For all of these, approximately,
f(P)dP
AP-4.5dP for some constant A. If all of
the volume is filled, then 1 =
f(P)dP, and the
average pressure is related to the minimum pressure as
Pave = 1.4Pmin, which means
f(P) = 1.15(P /
Pave)-4.5/Pave. Thus, the
probability that any of these regions has a pressure exceeding 10 times the
average, f(P > 10Pave), is 0.31
× 0.13.5 ~ 10-4;
similarly, f(P > 2Pave) ~
0.03. Evidently, most pressure bursts
from HII regions, winds and supernovae are within twice the average ISM
pressure for most of their lives. Therefore the external pressure is
important for them.
Kim, Balsara &
Mac Low (2001)
ran numerical simulations of the ISM and found that most of the time,
the pressure stayed within a factor of 2 of the average value.
The probability distribution function for pressure also suggests that the largest pressure bursts are close-range and short-lived. Thus significant over-pressures from stellar sources are most likely to occur close to those stars, as in an adjacent cloud. Most of the giant IR and HI shells discussed above are drifting by momentum conservation.
 |
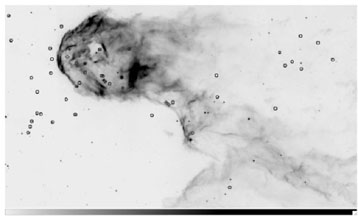Figure 2. A pillar in IC 1396 viewed at 8 µm with the Spitzer Space Telescope. Class I sources (the youngest) are identified by diamond shapes. There are three at the front of the head, one near the back part of the head, two on the lower part of the pillar and another in a shelf nearby (from Reach et al. 2009). |