4. AGE SEQUENCES IN BRIGHT RIMS

Several of the references above look for or find age sequences of stars along the axis of a bright rim. Sugitani, Tamura & Ogura (1995) pioneered this. At first, such a sequence seems obvious because the HII region is expanding, so position correlates with time. However, the bright-rim heads are usually more massive than the stars and the stars should be gravitationally attracted to the heads. If the head acceleration by gas pressure is less than their internal acceleration by gravity, then the embedded stars will get pulled along with the heads as the heads move. There would be little exposure of the stars in that case. To accelerate the head faster than the internal gravitational acceleration means that the pressure difference between the front and the back side has to exceed the internal gravitational acceleration multiplied by the head column density. Both of these quantities are essentially the internal self-gravitational binding energy of the head if the head is virialized, and therefore also the internal turbulent energy density. In that case, the head has to be accelerated faster than the square of its turbulent velocity dispersion divided by its radius. Such a larger acceleration could occur when the initially low-density gas is first compressed into a comet head by the HII region. Once the entire head is compressed and star formation occurs in the dense gas, the inside of the head will be close to pressure equilibrium with the outside ionization front, and the relative acceleration will decrease.

A description of such pressure equilibrium and the resulting acceleration is given by Bertoldi & McKee (1990). In their equation 5.10, they write the ratio of the self-gravitational acceleration inside the head to the acceleration of the whole head by the rocket effect as

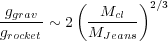(4.1)

for a non-magnetic head, and

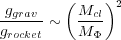(4.2)

for a magnetic head. Here, M_cl is the cloud head mass, M_Jeans = 1.18 _cl⁴ / (G³ P_cl)^1/2 and M = 0.12 / G^3/2 are the critical (or maximum) cloud masses for stability without and with a magnetic field, respectively; is the total magnetic flux in the cloud. The pressure at the ionized surface of the cloud enters the expression for M_Jeans and is

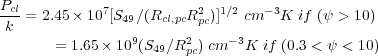(4.3) (4.4)

for dimensionless parameter ψ,

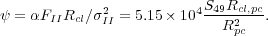(4.5)

In these expressions, the recombination rate to all but the ground state is , the incident ionizing flux is F_II in photons cm^-2 s^-1, the ionizing luminosity is S₄₉ in photons s^-1, the cloud radius is R_cl,pc in pc, the distance to the ionizing source is R_pc, in pc, the velocity dispersion in the cloud is _cl, and the velocity dispersion in the HII region is _II.

These equations suggest that if the cloud head requires gross instability for a star to form, i.e., M_cl > M_Jeans or M_cl > M (or, M_cl > M_Jeans + M in McKee (1989), then the internal gravitational acceleration in the head is always greater than the rocket acceleration. Thus the stars that form in the head should follow the head along as it accelerates away from the HII region. Why are the stars "left behind" in this case?

Another consideration is that the side of the dense core facing the HII region could be continuously peeled away by the ionization. The speed of this peeling is determined by the incident flux. After pressure equilibrium, a D-type ionization front enters the compressed neutral gas; "D" stands for density-bounded, i.e., the ionizing radiation is stopped by gas absorption (Spitzer 1978). The speed of such a front into the dense gas is _cl² / [2_II]. Because _II >> _cl, this D-front speed is always much less than _cl. The orbit speed of a newly formed star inside the head is of order _cl, however, for a self-gravitating head. Thus the speed at which the ionized side of the pillar gets peeled away is always much less then the embedded stellar speed. Thus, stars should not be exposed by ionization either.

Evidently, for both the rocket effect and ablation by ionization, stars forming in an unstable head should should continuously fall back into the head center faster than the surface of the head moves away from the source of ionization. This makes the exposure of young stars and their age gradients difficult to understand. It could explain, however, why age gradients are seldom obvious - the triggered stars scatter around the head by gravitational forces.

One solution to this problem is that the head is stable on a large scale with _cl equal to some turbulent speed that is larger than the sound speed, or perhaps with magnetic support, and yet inside of the head, there are local dense clumps that are unstable in the sense that their masses are larger than the thermal Jeans mass after the magnetic field has diffused out. In these cases, it might be possible that M_core > M_{Jeans,thermal} for localized star formation while at the same time g_grav < g_rocket for exposure of the star after it forms.

Another model of triggered star formation is that there is a pre-existing pillar-like shape with multiple clumps aligned to the HII region. Then the compression front moves along the pillar from clump to clump, triggering gravitational instabilities as it goes. The exposure of the stars would follow the erosion of each clump, compressed one after another.

Of course it is possible that the stars near the head were not triggered. A key observation for triggering will be the velocities of the young stars near the head in comparison to the head velocity. If the stars are moving much slower than the head, then they could have formed before the compression and rocket-like acceleration.

Simulations by Dale et al. (2007b) of triggered star formation in numerous dense clumps of a pre-existing molecular cloud indicate the difficulty in distinguishing between stars that formed previously and were exposed by clump ionization or motion, and stars that were triggered by the ionization pressure. In this study, the additional amount of star formation that was from the triggering alone was only ~ 30%.