5. TWO PROBLEMS: THE STAR FORMATION RATE AND THE INITIAL MASS FUNCTION

In this final section we'll come up to the present state of the art and talk about what are probably the two largest unsolved problems in star formation today: the star formation rate and the origin of the initial mass function.

5.1. The Star Formation Rate

5.1.1. The Observational Problem: Slow Star Formation

The problem of the star formation rate can be understood very simply. In the last lecture we computed the characteristic timescale for collapse to occur, and argued that, even if a collapsing region is only slightly unstable initially, this will not change the collapse time by much. Magnetic fields could delay or prevent collapse, but observations seem to indicate that they are not strong enough to do so. Thus we would expect that, on average, clouds will collapse on a timescale comparable to t_ff, and the rate of star formation in a galaxy should be the total mass of bound molecular clouds M divided by this.

To make this more concrete, we introduce the notation (first used by Krumholz & McKee [22])

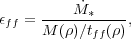(138)

where M() is the gas mass in a given region with density or larger, t_ff is the free-fall time evaluated at that density, and _* is the star formation rate in the region in question. The regions here can be either entire galaxies are specified volumes within a galaxy. We refer to _ff as the dimensionless star formation rate or star formation efficiency. Unfortunately the language here is somewhat confused, because people sometimes mean something different by star formation efficiency. To avoid confusion we will just use the symbol _ff.

The argument we have just given suggests that _ff should be of order unity if we pick to be the typical density of molecular clouds, or anything higher. However, the actual value of _ff is much smaller, as first pointed out by Zuckerman & Evans [23]. The Milky Way's disk contains ~ 10⁹ M of GMCs inside the Solar circle [24, 25], and these have a mean density of n ~ 100 cm^-3 [26], corresponding to a free-fall time time t_ff 4 Myr. Thus M / t_ff 250 M yr^-1. The observed star formation rate in the Milky Way is ~ 1 M yr^-1 [27, 28]. Thus _ff ~ 0.01! Clearly our naive estimate is wrong.

One can repeat this exercise in many galaxies and using many different density tracers. One way is to measure the mass using a molecular tracer with a known critical density, which effectively gives M(), compute t_ff() at that critical density, and compare to the star formation rate. Krumholz & Tan [29] compiled the data available at the time and found that, for every tracer for which they could make a measurement, and in every galaxy, _ff was still ~ 0.01 (Figure 6). Subsequent more accurate measurements in several large surveys, most notably the c2d survey [30], give the same result. Thus, we have a problem: why is the star formation rate about 1% of the naively estimated value?

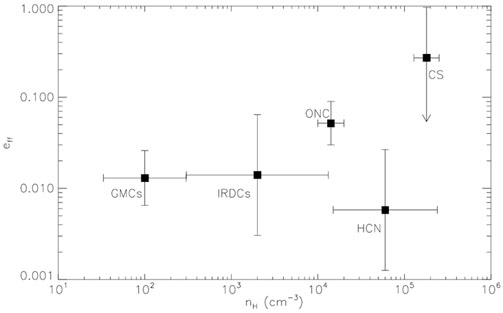Figure 6. Observed star formation efficiency per free-fall time ff, as a function of mean gas density nH. Each data point represents a different method of measuring the gas, which is sensitive to different densities. GMC indicates giant molecular clouds, traced in CO J = 1 0. IRDCs indicates infrared dark clouds, measured in infrared absorption. ONC is the Orion Nebula cluster, a single star cluster near Earth, whose gas mass is estimated from the mass and dynamical state of the remaining star cluster. HCN represents extragalactic measurements in the HCN J = 1 0 line. Finally, CS represents measurements of the CS J = 5 4 line within the Milky Way. However, it is only an upper limit. Reprinted with permission from the AAS from [29].

As a side note, the famous Kennicutt relation [31], which is an observed correlation between the star formation rate in a given portion of a galaxy disk and the gas surface density in that region. The observed normalization of the Kennicutt relation is equivalent to the statement _ff ~ 0.01.

5.1.2. Potential Solutions

There are two major classes of proposed solution to this problem. One is the idea that molecular clouds aren't really gravitationally bound, and the other is the idea that clouds are bound, but that turbulence inhibits large-scale collapse while permitting small amount of mass to collapse.

Unbound GMCs   The unbound GMC idea is that most of the mass in molecular clouds is in a diffuse state that is either not gravitationally bound, or that is supported against collapse by strong magnetic fields. (The latter is not ruled out because it is not easy to measure the magnetic field in very diffuse molecular gas.) This idea would definitely work, in the sense that it would produce low star formation rates, if GMCs really were unbound. The main problem is that there is no observational evidence that this is the case, and considerable evidence that it is not. In particular, while we have no trouble finding low mass CO-emitting clouds with virial ratios _vir >> 1, CO-emitting clouds with masses 10⁴ M and _vir >> 1 do not appear to exist [32]. If GMCs were really unbound, why do they all have virial ratios ~ 1?

A second problem with this idea is that, as we have seen _ff is ~ 1% across of huge range of densities and environments. It is not at all obvious why the fraction of mass that is bound would be the same at all densities and across all galactic environments, from low-mass dwarfs to massive ultraluminous infrared galaxies. The universality of the ~ 1% seems to demand an explanation that is rooted in something more universal than an appeal to fractions of a GMC that are bound versus unbound.

Turbulence-Regulated Star Formation   A more promising idea, which is probably the most generally accepted at this point (though it still has significant problems) is that the ubiquitous turbulence observed in GMCs serves to keep the star formation rate within them low. The first quantitative model of this in the hydrodynamic case was proposed by Krumholz & McKee [22], and it has since been extended to the MHD case by Padoan & Nordlund [33].

The basic idea of this model relies on two properties of supersonic turbulence. Due to time limitations we will not prove these, but they can be understood analytically, and the are reproduced in every simulation. The first property is that turbulence obeys what is known as a linewidth-size relation. This means that, if we consider a region of size and compute the non-thermal velocity dispersion _nt within it, the velocity dispersion will depend on . For subsonic turbulence the relationship is _nt ^1/3, while for highly supersonic turbulence it is ^1/2. This relationship is in fact observed in molecular clouds.

Now consider the implications of this result in the virial theorem. On large scales we know that clouds have _vir ~ 1, so that || ~ . If we consider a random region within a cloud of size < R, where R is the cloud radius, then the mass within that region will scale as ³, so the gravitational potential energy will scale as M² / ⁵. In comparison, the kinetic energy varies as M ^{2 4}, since ² for large . Thus we expect that, for an average region

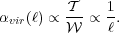(139)

Since _vir(R) 1, this means that _vir >> 1 for l << R, i.e. the typical, randomly chosen region within a GMC is gravitationally unbound by a large margin. This is in good agreement with observations: GMCs are bound, but random sub-regions within them are not.

We can turn this around by asking how much denser than average a region must be in order to be bound. For convenience we define the sonic length as the choice of length scale for which the non-thermal velocity dispersion is equal to the thermal sound speed, i.e.

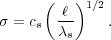(140)

Now consider a region within a cloud with density , chosen small enough that the velocity dispersion is dominated by thermal rather than non-thermal motions. The maximum mass that can be supported against collapse by thermal pressure is the Bonnor-Ebert mass. If we let be the density at the surface of our Bonnor-Ebert sphere and we adopt a uniform sound speed c_s, then = c_s, P_s = c_s², and

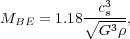(141)

and the corresponding radius of the maximum mass sphere is

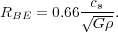(142)

We can compute the gravitational potential energy and the thermal energy of such a sphere from its self-consistently determined density distribution. The result is

(143) (144)

Similarly, we can compute the turbulent energy from the linewidth-size relation evaluated at = 2 R_BE. Doing so we have

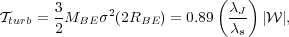(145)

where _j = ( c_s² / G )^1/2 is called the Jeans length; it is just 2.7 times R_BE.

This is a very interesting result. It says that the turbulent energy in a maximal-mass Bonnor Ebert sphere is comparable to its gravitational potential energy if the Jeans length is comparable to the sonic length. Since the Jeans length goes up as the density goes down, this means that, at low density, _turb >> |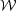|, while at high density _turb >> |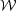|. In order for a region to be unstable to collapse, the latter condition must hold. We have therefore identified a minimum density at which we expect sub-regions of a molecular cloud to be unstable to collapse.

To get a sense of what this density is, let us evaluate _j / _s at the mean density of a 10⁴ M, 6 pc-sized molecular cloud. If such a cloud has _vir = 1, the velocity dispersion at the cloud scale is = 1.2 km s^-1; since c_s = 0.2 km s^-1, we have _s = 0.15 pc. At the mean density of the cloud, = 7.5 × 10^-22 g cm^-3, and _j = 1.5 pc. Thus _j >> _s, and at the mean density things are unbound by a large margin. To be dense enough to be bound, the density has to be larger than the mean by a factor of (_s / _j)² 100, so bound structures are those with 8 × 10^-20 g cm^-3, or n 3 × 10⁴ cm^-3.

In order to go further we must know something about the internal density distribution in molecular clouds. We now invoke the second property of supersonic isothermal turbulence: it generates a distribution of densities that is lognormal in form. Formally, the point probability distribution function of the density, meaning the probability of measuring a density at a given position, obeys

(146)

where x = / is the density divided by the volume-averaged density, = -² / 2 is the mean of the logarithm of the overdensity, and is the dispersion of log density. That the density distribution should be lognormal isn't surprising. In a supersonically turbulent medium, each shock that passes a point multiplies its density by a factor of the Mach number of the shock squared, and each rarefaction front divides the density by a similar factor. Thus the density at a point is a product of many multiplications and divisions, and by the central limit theorem the result of many such operations is a lognormal (just as the result of doing many random additions and subtractions is a normal distribution). Empirical work shows that the width of the normal distribution depends on the Mach number of the turbulence as

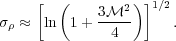(147)

Now we can put together an estimate of the star formation rate. We estimate that the gas that has a density larger than the critical density given by the condition that _j < _s, which is

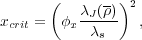(148)

where _x is a factor of order unity. If we compute the mean density and the sonic length for our fiducial cloud of mass M, radius R, and velocity dispersion , with a little algebra we can show that

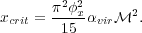(149)

Gas above this density forms stars on a timescale given by the free-fall time at the mean density, since that is the timescale over which the density distribution will be regenerated to replace overdense regions that collapse to stars. Thus we have

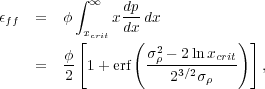(150) (151)

where is another constant of order unity. Note that, except for the factors, everything in this expression is given in terms of _vir and , i.e. in terms of the virial ratio and Mach number of the cloud. The factors can be calibrated against simulations. For those who don't walk around with graphs of the the error function in their heads (i.e. most of us), it's useful to have a powerlaw approximation to this, which is

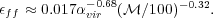(152)

In other words, for a cloud with ~ 10-100 and _vir = 1, we expect _ff ~ 0.01, which nicely explains the observation that _ff ~ 0.01 everywhere. This analytic model also agrees well with numerical simulations [33].

Driving Turbulence   This is a cute explanation, but it assumes that the turbulence is present and is capable of inhibiting star formation over the lifetime of a molecular cloud. This is not obvious, because we know from numerical experiments that turbulence decays quickly. This is not surprising. Every time there is a shock, kinetic energy is converted into thermal energy. Because radiative times are short compared to mechanical ones, as we showed earlier, all this energy is radiated away immediately, bringing the gas back to its original temperature. This represents a net loss of energy, and in the absence of a source to offset this loss the turbulence must decay. Numerical experiments show that the decay time is only about a crossing time of the cloud [14].

We therefore need an energy source to drive the turbulence. There are two main possibilities, both of which probably contribute. One is the gravitational potential energy released in the formation of the molecular cloud itself. As material falls onto the cloud it can drive turbulent motion, and as long as the cloud gains mass quickly from the larger ISM that is probably an important energy source [34, 35]. A second source, which is probably more important in evolved GMCs, is feedback from newly formed stars. Young stars produce strong jets that can drive motions in their parent clouds [36, 37], and they also produce ionizing radiation that can drive motions [38, 39]. Both of these effects can drive turbulence, and they probably dominates in more evolved clouds. Exactly what the energy balance in GMCs is, and how it is maintained, is not completely understood.

5.2. The Initial Mass Function

5.2.1. The Observed IMF

Our second unsolved problem in this lecture is the initial mass function (IMF). To begin, we have to define what the IMF means. It is simply the mass distribution of a population of stars at birth. We define this by a function

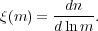(153)

Note that dn / dm would be the number of stars per unit mass, while (m) = dn / d ln m = m (dn / dm) is the mass of stars per unit mass, i.e. _m1^m₂ (m) dm is the fraction of the mass in a newborn stellar population that is found in stars with masses between m₁ and m₂.

Observing the IMF is tricky, and there are three main approaches. One is to look at a young cluster and count the stars in it as a function of mass. This is the most straightforward approach, but it is limited by the number of young clusters where we can directly measure individual stars down to low masses. This means that we get a clean measurement, but the statistics are poor. A second approach is to rely on counts of field stars in the solar neighborhood that are no longer in clusters. Here the statistics are much better, but we can only use this technique for low mass stars, because for massive ones the number in the Solar neighborhood is determined more by star formation history than by the IMF. Finally, we can get limits on the IMF from the integrated light of a stellar populations.

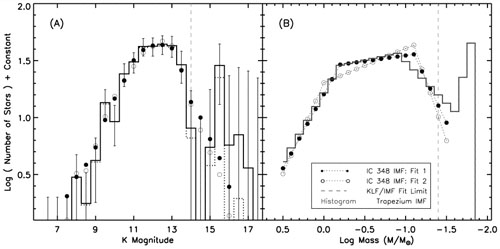Figure 7. Measured K band luminosity functions (left) and stellar initial mass functions (right) for the cluster IC 348 (filled and open circles), and for the Trapezium cluster (histogram). Reprinted with permission from the AAS from [40].

One interesting result to come out of all of this work is that the IMF is remarkably uniform. One can notice this at first by comparing the mass distributions of stars in different clusters. As Figure 7 illustrates, clearly the two clusters IC 348 and the Trapezium have the same IMF for the mass range they cover. This is despite the fact that the Trapezium is a much larger, denser cluster forming out a significantly larger molecular cloud. The Trapezium IMF is also a good fit in a remarkably broad range of even more different environments. For example, it is a good fit to the stellar mass distribution in the Digel 2 North and South clusters, which are forming in the extreme outer galaxy, R_gal 19 kpc [41]. We also obtain a good fit using this IMF to model globular clusters, provided that we account for the age of the stellar population and for dynamical effects such as evaporation and mass segregation [42]. This represents a star-forming environment that is much denser, at much lower metallicity, out of the galactic plane rather than in the plane, and at much higher redshift, yet has the same IMF. All of these IMFs also agree with the IMF derived for field stars in the solar neighborhood. Thus one constraint on theories of the IMF is that, at least on the scale of star clusters or larger, it is remarkably universal. There is some indirect evidence for variation of the IMF at the very high end, although I would describe it as suggestive rather than definitive, and we won't go into it.

The observed IMF can be parameterized in several ways; popular parameterizations are due to Kroupa (2002) and Chabrier et al. (2003). All parameterizations share in common that they have a powerlaw tail at high masses with

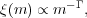(154)

with 1.3 - 1.4. At lower masses there is a flattening, reaching a peak around ~ 0.2-0.3 M, and then a decline at still lower masses, although that is very poorly determined due to the difficulty of finding low mass stars. This is parameterized either with a series of broken powerlaws or with a lognormal function [43, 44, 45]. Figure 8 shows a plot of one proposed functional form for (m) (due to [43]).

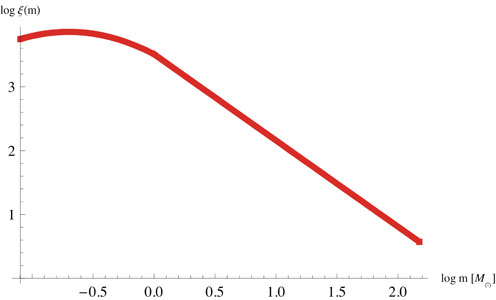Figure 8. An IMF (m) following the functional form proposed by [43].

5.2.2. The IMF in the Gas Phase?

What is the origin of this universal mass function? The biggest breakthrough in answering this question in the last several years has come not from theoretical or numerical advances (although those have certainly helped), but from observations. In particular, the advent of large-scale mm and sub-mm surveys of star-forming regions has made it possible to assemble statistically significant samples of overdense regions, or "cores", in star-forming clouds.

The remarkable result of these surveys, repeated using many different techniques in many different regions, is that the core mass function (CMF) is the same as the IMF, just shifted to slightly higher masses. The cleanest example of this comes from the Pipe Nebula, where Alves et al. [46] used a near-infrared extinction mapping technique to locate all the cores down to very low mass limits at very high spatial resolution. Finding all the cores in the Pipe shows that their mass function matches the IMF, including a powerlaw slope of -1.35 at the high end, a flattening at lower masses, and a turn-down below that. The distribution is shifted to higher mass than the IMF by a factor of 3 (Figure 9). This is the cleanest example, but it is not the only one. Similar results are obtained using dust emission in the Perseus, Serpens, and Ophiuchus clouds [47].

Figure 9. Left: extinction map of the Pipe Nebula with the cores circled. Right: mass function of the cores (data points with error bars) compared to stellar IMF (solid line). Reprinted with permission from [46].

5.2.3. A Possible Model: Turbulent Fragmentation and Radiation-Suppressed Fragmentation

Although we don't have a complete model that meets the three conditions outlined above, we can sketch out the beginnings of one. This may be entirely wrong, but it's the idea that, right now, I consider the most promising.

The Padoan & Nordlund Model for the CMF   The model's basic elements were originally proposed by Padoan & Nordlund [48]. The first element is the idea that supersonic turbulence generates a spectrum of structures with a slope that looks similar to the high end slope of the stellar IMF. Formally, one can show (though we will not in this lecture) that the distribution of fragment masses follows a distribution

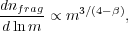(155)

where is a numerical factor related to the exponent q in the linewidth-size relation by = 2q + 1. (Formally is the index of the turbulent power spectrum, so if we have a linewidth-size relation v ^q, then one can show that the power spectrum is P(k) k.) To remind you, for subsonic turbulence q 1/3 and for highly supersonic turbulence q 1/2, corresponding to = 5/3 or = 2, respectively. At the Mach numbers in molecular clouds tends to be a bit less than 2, around 1.9, giving a slope around 1.4. Notice that this is very similar to the observed high-mass slope ~ 1.3 - 1.4.

By itself this is just a pure powerlaw. However, not all of the structures generated by the turbulence are gravitationally bound and liable to collapse. The very massive ones almost certainly are, because their masses are larger than the Bonnor-Ebert mass for any plausible surface pressure. However, the low mass ones are bound only if they find themselves in regions of high pressure, which lowers the Bonnor-Ebert mass to a value smaller than the mean in the cloud.

To make this more quantitative, recall our result that the distribution of densities inside a molecular cloud, and thus this distribution of pressures (since P in an isothermal gas), is lognormal. Thus the number of stars formed at a given mass is given by the number of fragments of that mass produced by the turbulence multiplied by the probability that each fragment generated is bound:

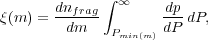(156)

where P_min is the minimum pressure required to make an object of mass m unstable, and dP / dp is the (lognormal) distribution of pressures. The effect of this integral is to impose a lognormal turndown on top of the powerlaw produced by turbulence. Simulations seem to show fragments forming in a manner and with a mass distribution that is in good agreement with this model (Figure 10).

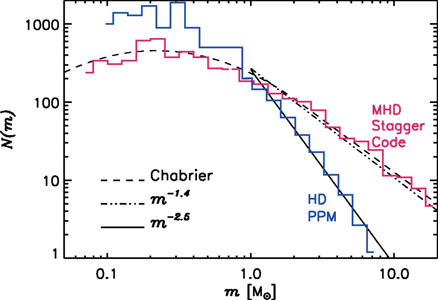Figure 10. The distribution of core masses produced in a simulations of turbulence, using hydrodynamics (blue) and magnetohydrodynamics (red). The overplotted dashed line shows the IMF, using the functional form of [43]. Reprinted with permission from the AAS from [49].

The answer to that problem was provided in a series of papers by Krumholz et al. [51, 52, 53, 54]. Inside a collapsing core a first low mass star will form, and as matter accretes onto it, the accreting matter releases its gravitational potential energy as radiation. This is a lot of radiation. In a massive core the velocity dispersions tend to be supersonic, and the corresponding accretion rates ~ ³ / G are large, perhaps ~ 10^-4 - 10^-3 M yr^-1. If one drops mass at this rate onto a protostar of mass M and radius R, the resulting luminosity is

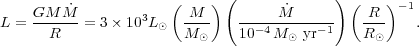(157)

With a source of this luminosity shining from within it, a massive core is no longer isothermal. Instead, its temperature rises, raising the sound speed and suppressing the formation of small stars - recall that, in an isothermal gas, M_BE c_s³ T^3/2. Then the problem becomes a dynamical one, in which there is a competition between secondary fragments trying to collapse and the radiation from the first object trying to raise their temperature and pressure to disperse them. One can study this result using radiation-hydrodynamic simulations, and the result is that, for sufficiently dense massive cores, the heating tends to win, and massive cores tend to form binaries, but fragment no further. (This latter point is good, because essentially all massive stars are observed to be binaries.)

A final difficulty with massive cores is radiation pressure. A cartoon version of the problem can be understood as follows. Massive stars have very short Kelvin times, so they will reach the main sequence and begin hydrogen burning while they are still accreting. Now consider the force per unit mass exerted by the star's radiation on the gas around it. This is

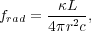(158)

where is the opacity per unit mass. We can compare this to the gravitational force per unit mass

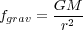(159)

to form the Eddington ratio

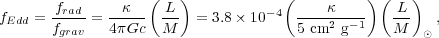(160)

where the value of we've plugged in is typical for dusty interstellar gas absorbing near-IR photons. Thus we expect radiation force to exceed gravitational force once the star has a light to mass ratio larger than a few thousand in Solar units. This happens at a mass M ~ 20 M.

So how can bigger stars form, when they should repel rather than attract interstellar matter? This is a classic problem in star formation, and it led to all sorts of exotic theories for how massive stars form, e.g. that they form via stellar collisions in dense clusters. If any of these models are right, then the picture we've just outlined cannot be correct. Fortunately, it turns out that there is a more prosaic answer. Real life is not spherically symmetric, and using radiation to try to hold up infalling gas proves to be an unstable situation. The instability is not all that different from garden variety Rayleigh-Taylor instability, with radiation playing the role of the light fluid (Figure 11).

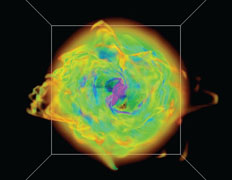Figure 11. A volume rendering of the gas density a simulation of a the formation of a massive binary star system, showing the accretion disk face-on (left) and edge-on (right). Notice the Rayleigh-Taylor fingers that channel gas onto the accretion disk. Reprinted with permission from [50].