4. STAR FORMATION PROCESSES IN THE RING

4.1. The Role of Gravitational Instabilities

The onset of robust star formation in gas disks can be described in terms of local gravitational stability parameters, e.g., Q_gas = _gas / ( G _gas), where _gas is the gas velocity dispersion and is the disk's epicyclic frequency (Quirk 1972). Regions of the disk where Q_gas < 1 are Jeans unstable and prone to collapse, leading to the formation of molecular cloud complexes and eventually stars. The "bead on a string" morphology evident in H (Figure 1) suggests that the rings are gravitationally unstable. Are they?

The Cartwheel's ring is, even ignoring its (unknown) molecular component. However, Q_gas > 1 essentially everywhere in L-S'a ring (Figure 3), due to the large _gas. This ignores, however, the stellar component's contribution to Q. Using IRAC 4.5 µm data we find that the stellar mass surface density (_*) everywhere exceeds that of gas (i.e., _* > _HI + _H2). A gravitational stability parameter combining stars and gas can be written Q_tot = ( / G) ( _gas / _gas + _* / _*)^-1 (Wang & Silk 1994), where the ring's radial H profile constrains _* 45 km s^-1. Figure 3 shows that when the stellar component is included, Q_tot < 1 and L-S's ring is everywhere Jeans unstable.

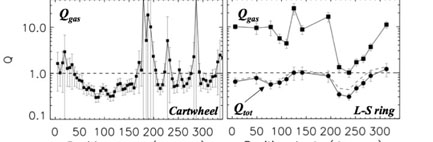Figure 3. Azimuthal variations in Q for Cartwheel (left) and L-S (right). The Cartwheel's HI ring is largely sub-critical (Qgas < 1), but not L-S even after adding molecular gas. Only when stellar mass is included does the ring become gravitationally unstable (i.e., Qtot < 1) everywhere.

4.2. Evidence for Peculiar Star Formation Laws

A strong correlation exists between SFR / area (_SFR) and the surface density of cold gas in galaxies, i.e., the "Schmidt Law", written _SFR = _gas^N. In M 51 for example, H₂ and SFR / area obey _{SFR H2}^{1.37 ± 0.03} (Figure 4). HI is uncorrelated with _SFR, implying that it is a photo-dissociation product and not directly involved in the star formation process. We show star formation laws derived for the Cartwheel and L-S in the same figure. Both are peculiar. Unlike M 51, atomic gas in the Cartwheel correlates with _SFR in most of the ring, though with a small N. The exponent becomes negative (i.e., anti-correlated) where _SFR peaks. Would this peculiarity disappear if the molecular component were available? Not if L-S's ring is any guide: atomic gas obeys M 51's molecular Schmidt Law, but its cold molecular ISM is uncorrelated with _SFR, which is completely the opposite from M 51. How can H₂ be so apparently disconnected from star formation?

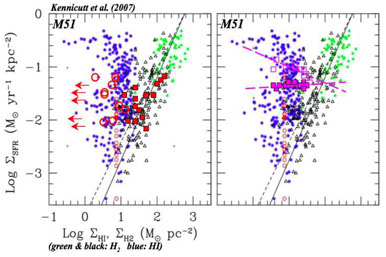Figure 4. Star formation laws in the rings of L-S (left) and Cartwheel (right) relative to M 51 (Kennicutt et al. 2007). H2 in M 51 (black & green triangles) obeys a Schmidt Law, but HI (blue) is uncorrelated with SFR. In L-S the opposite is true: HI (red squares) obeys a Schmidt Law but H2 is uncorrelated (red circles & arrows). In Cartwheel atomic gas can be correlated (filled purple squares) or anti-correlated (empty squares) with SFR / area.

4.3. Enhanced Star Formation Efficiencies

Star formation efficiency (SFE) is the yield of massive stars per unit H₂ mass. Young et al. (1996) find nearly constant SFE ( log(L_H / M_H2)) from S0 to Scd ( -1.8 L / M). Later types show higher SFE, peaking at -0.8 L / M for Irr. Detecting molecular gas in L-S's ring allows the first estimate of SFE in a ring galaxy. We find SFE = -0.7 ± 0.1 L / M, i.e., similar to an Irr and an order of magnitude higher than the (presumably ~ Sa) progenitor. This result depends, of course, on our ability to reliably measure H₂ in the ring using ¹²CO emission.