


The problem with existing brute force approaches to modeling star formation and feedback within the context of galaxy cluster simulations is that they produce too few galaxies per cluster (unless extraordinarily high resolution is used), the galaxies form stars at too high a rate at late time (i.e., they are blue when they should be red), and the fraction of a cluster's baryonic mass in stars is too high [72]. In this section we highlight a new approach to incorporating galaxies and their feedbacks into hydrodynamic cosmological simulations of galaxy clusters which improves the agreement between simulated and observed clusters [79, 80]. The key idea is rather than attempt to simulate the internal processes of galaxies, these are modeled analytically or taken from observations. This is done through the introduction of a galaxy construct (Galcon)-one per galaxy dark matter halo-whose motion through the cluster is simulated as an N-body of finite size and mass, but whose internal processes are programmable. The star formation history of each Galcon is an input function rather than an output. This ensures agreement with observations. Feedbacks of energy and metals is taken to be proportional the the instantaneous star formation rate, again calibrated by observations. Feedback is done in a well-resolved spherical shell at the Galcon's outer radius rather than from an unresolved point source, which ensures that the energy and metals get out into the IGM. Finally, and perhaps most importantly, a cluster with hundreds if not thousands of galaxies can be simulated economically because the mass and spatial resolution requirement is not so high. One requires only enough resolution to be able to find the galaxy dark matter halos at high redshift which fall into the cluster.
Fig. 16 shows the results of a Galcon simulation described in more detail in [79, 80]. The procedure is as follows. We set up a standard Enzo simulation of a single galaxy cluster including dark matter, gas but no radiative cooling and in situ star formation and feedback. In order to achieve the required mass and spatial resolution in the cluster forming region we employ the nested grid+AMR strategy described in Sec. 4. We run this simulation to the "replacement redshift" of z = 3, where the output is analyzed for galaxy dark matter halos. For each halo we introduce a Galcon with an analytic mass model for stellar and gas distibution derived from a fit to the simulated baryon distribution. We then restart the simulation and run it to z = 0. We assume each Galcon's star formation history follows the observationally determined cosmic star formation history with an appropriate weighting reflecting its mass. Mass loss through galactic winds and ram pressure stripping are modeled analytically.
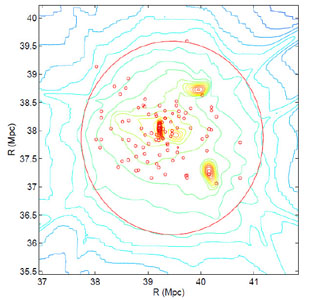 |
Figure 16. Galaxy cluster simulation using Galcons. Galcons, short for galaxy constructs, are programmable subgrid models for galaxies that have finite mass and size, are evolved kinematically as N-bodies, and feed back mass, energy, metals, etc. to the ICM through a resolved spherical boundary at their extremities. Small circles denote the location of 89 galcons, superimposed on a contour map of the baryon density. Large circle denotes the virial radius of the cluster. From [79]. |
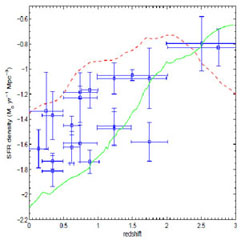
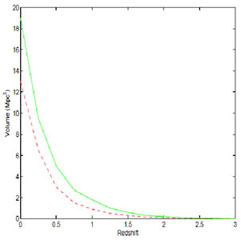
The upper left panel in Fig. 17 compares the SFR density in the Galcon simulation with another Enzo simulation with identical initial conditions but using the star formation and feedback recipe of Cen & Ostriker (1992). Observational data points are also superposed. We see a sharply declining SFR in the Galcon simulation after z = 3, while the standard simulation rises and remains quite high to z = 0 in conflict with observations. Since feedback by galactic winds is assumed to be proportional to the SFR, this implies that the ICM in the two simulations have very different heating histories. In the standard simulation, the heating is confined to a small number of massive, centrally located galaxies late in time. In the Galcon simulation heating occurs early in an extended region of space by nearly 100 galaxies before the cluster collapses. This difference can be seen by comparing the redshift evolution of the volume of gas being heated by galaxy feedback (Fig. 17, upper right panel).
 |
 |
 |
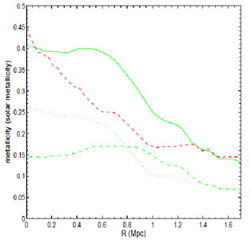 |
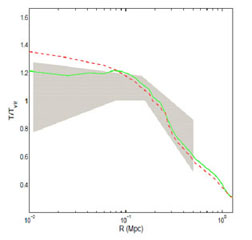
Figure 17. Contrasting a Galcon cluster simulation (green solid lines) with a simulation using a well-known recipe for in situ star formation and feedback (red dashed lines). Top left: star formation rate density versus redshift. Top right: volume of feedback regions versus redshift. Bottom left: spherically averaged radial temperature profile. Shaded grey region bounds observed profiles from a sample of 15 clusters from [104]. Bottom right: Metallicity profiles at z=0. Contributions to the total metallicity from galactic winds (dashed-dotted green line) and due to ram pressure stripping (dashed green line) are shown as well. From [80]. |
|
The different heating histories and spatial distribution has an effect on the spherically averaged gas temperature profiles at z = 0, as shown in the lower left panel of Fig. 17. The Galcon simulation produces an isothermal core out to r = 0.1 rvir, while the standard simulation produces a temperature profile which continues to rise to smaller radii. The former is in better agreement with observations (shaded region), although still a bit high in the core region, while the latter appears to be inconsistent with observations.
The different feedback histories in the two simulations are also
reflected in the different metallicity profiles at z=0 shown in lower
right panel of Fig. 17.
The Galcon simulation produces a flat metallicity profile at Z =
0.4 Z out to a radius of 600 kpc, in good agreement with observations, while
the standard simulation shows a sharply declining metallicity
gradient. This difference can be understood by looking at the
conribution of metals due to galactic winds and ram pressure stripping
in the Galcon simulation, shown as two separate curves in
Fig. 17. A metallicity floor of about Z
= 0.15 Z
out to a radius of 600 kpc, in good agreement with observations, while
the standard simulation shows a sharply declining metallicity
gradient. This difference can be understood by looking at the
conribution of metals due to galactic winds and ram pressure stripping
in the Galcon simulation, shown as two separate curves in
Fig. 17. A metallicity floor of about Z
= 0.15 Z is contributed by galactic winds driven by early star formation when the
galaxies where spatially extended. Ram pressure stripping removes metal
enriched ISM gas from the Galcons and deposits it preferentially in the
central regions of the cluster at late times where the ICM gas is denser.
is contributed by galactic winds driven by early star formation when the
galaxies where spatially extended. Ram pressure stripping removes metal
enriched ISM gas from the Galcons and deposits it preferentially in the
central regions of the cluster at late times where the ICM gas is denser.
This model can be significantly improved upon in several ways. First, Galcons could be introduced dynamically rather than at one time, and starting earlier. This would require running a halo finder inline with the calculation, which we can now do with Enzo [81]. Second, we could import star formation histories more appropriate to cluster galaxies, rather than assume the globally average rate. If one believes that Lyman break galaxies are the precursors of cluster galaxies [109], then their high rates of star formation and strong outflows would provide more heating and hence higher entropies in the cluster core than we have simulated. This could help establish the observed entropy floor that current simulations fail to produce. Finally, we could allow our Galcons to merge using simple kinematic rules, which we presently do not do. We could introduce a burst of star formation in a way which is consistent with observations, and possibly even fuel AGN activity which could provide extra heating.
5.2. AGN Feedback: X-ray Cavity Formation by a Magnetized Jet
High-resolution X-ray images of galaxy clusters by Chandra have revealed giant cavities and weak shock fronts in the hot gas [82, 83, 84] which are commonly associated with energetic radio lobes [85, 86] and suggest that magnetic fields play an important role. Numerical simulations of hot, underdense bubbles in galaxy clusters have been performed by a number of authors [87, 88, 89, 90]. It is generally possible to inject a large amount of energy into the ICM via AGNs, but it is not exactly clear how the AGN energy can be efficiently utilized [91]. One of the most interesting characteristics of the radio bubbles is that they are intact, whereas most hydrodynamic simulations [95, 89, 96] have shown that purely hydrodynamic bubbles will disintegrate on timescales of much less than 108 yr, markedly different from observations.
Using the first cosmological AMR MHD simulations, Xu et al. (2008) [105] have shown that intact X-ray cavities can be produced with properties similar to those observed [82, 83]. The simulations model the formation of a galaxy cluster within its proper cosmological context with magnetic energy feedback from an active galactic nucleus (AGNs). The X-ray cavities are produced by the magnetically dominated jet-lobe system that is supported by a central axial current. The cavities are magnetically dominated, and their morphology is determined jointly by the magnetic fields and the background cluster pressure profile. The expansion and motion of the cavities are driven initially by the Lorentz force of the magnetic fields, and the cavities only become buoyant at late stages (1500 Myr). Interestingly, Xu et al. find that up to 80-90% of the injected magnetic energy goes into doing work against the hot cluster medium, heating it, and lifting it in the cluster potential.
The simulation used the newly developed cosmological AMR-MHD module for the Enzo code described in [97]. The procedure is evolve a galaxy cluster from cosmological initial conditions to z = 0.05. Magnetic feedback of a SMBH in the cluster center is modeled by injecting both poloidal and toroidal magnetic flux in a divergence-free way into the central few kpc for 3 × 107 yr. The magnetic configuration is not force-free, but rather develops bipolar magnetically dominated "towers" that extend along an axis. The total amount of magnetic energy injected is 6 × 1060 erg. After the source switches off, the cluster is evolved for another 650 Myr.
Fig. 18 shows snapshots of the jet-lobe evolution driven by the magnetic energy output of an AGN. Each image is 672 kpc on the side. Columns from left to right are slices of density, temperature, the averaged magnetic energy density, and the integrated X-ray luminosity, respectively. The top row shows the cluster with the jet lobe at the end of magnetic energy injection. The middle and bottom rows show the well-developed bubbles moving out of the cluster center. The bubbles are driven by magnetic forces at all stages and might become buoyant only after t > 500 Myr. As can be seen, the X-ray cavities remain intact with sharply defined boundaries until the end of the simulation.
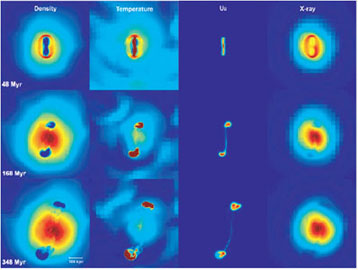 |
Figure 18. Snapshots of the jet-lobe evolution in a realistic cluster ICM driven by the magnetic energy output of an AGN. Each image is 672 kpc on a side. Columns from left to right are slices through the cluster center of gas density, gas temperature, magnetic energy density, and X-ray emissivity. Rows correspond to evolutionary times after the turn-on of the AGN, which remains in the on state for 36 Myr. As can be seen, well defined X-ray cavities with sharp, smooth boundaries are formed which remain intact for hundreds of Myr as they bouyantly rise through the ICM. From [105]. |
It is now appreciated that a non-negligible fraction of a cluster's binding energy is in the form of fluid turbulence. Major mergers are the most likely source of energy, stirring the ICM on scales approching the virial radius. Direct evidence for cluster turbulence would be Doppler broading of X-ray lines, or the kinetic SZ effect [68]. As yet, these velocity signatures have not been detected due to instrumental limitations. Indirect evidence is the strong magnetic fields observed in cluster cores via Faraday rotation measurements (see discussion below). Here, strong fields would be the result of turbulent amplification of some small seed field.
Cluster turbulence was first studied by Norman & Bryan (1999)
[98]
using the newly developed ENZO AMR code.
They simulated the formation of a rich cluster in a SCDM cosmological
model assuming non-radiative gas dynamics. They found turbulent
velocities and bulk flows in the core of around 0.25
 vir,
increasing to as large as 0.6
vir,
increasing to as large as 0.6
 vir near the
virial radius. This translates into a turbulent
pressure of about 10% of the total in the core region, increasing to
about 30% near the virial radius, although distinguishing between what
is an ordered versus a disordered flow becomes problematic near the
virial radius. These results were broadly confirmed through the Santa
Barbara Cluster code comparison project, in which a number of different
numerical methods were applied to evolve a common set of initial
conditions leading to the formation of a Coma-like cluster
vir near the
virial radius. This translates into a turbulent
pressure of about 10% of the total in the core region, increasing to
about 30% near the virial radius, although distinguishing between what
is an ordered versus a disordered flow becomes problematic near the
virial radius. These results were broadly confirmed through the Santa
Barbara Cluster code comparison project, in which a number of different
numerical methods were applied to evolve a common set of initial
conditions leading to the formation of a Coma-like cluster
Recently Vazza et al. (2009) [108] have implemented a new adaptive mesh refinement criterion into Enzo based on velocity jumps that provides higher resolution within the cluster virial radius and thus a better characterization of the turbulent state of the ICM gas. They found an outer scale for the turbulence of about 300 kpc and a velocity power spectrum consistent with Kolmogorov for incompressible turbulence Ek ~ k-5/3. They found that compared to the standard density-based refinement criterion, their clusters have lower central gas densities, flatter entropy profiles, and a higher level of turbulence at all radii. The ratio of turbulent kinetic energy to thermal energy is found to be ~ 5 percent within 0.1 Rvir, increasing to ~ 10-20 percent within Rvir. The trend of increasing levels of turbulence with radius is consistent with Norman & Bryan (1999), however the absolute levels are somewhat lower because Vazza et al. did a more careful job separating the velocity field into bulk and turbulent components. They find bulk flows (velocity fields which are ordered on scales of 300 kpc or more) also contribute substantially to the nonthermal energy budget, consistent with the findings of Norman & Bryan (1999).
Fig. 19 shows the velocity field on a slice through the cluster center, and Fig. 20 shows radial profiles of turbulent, bulk kinetic, and thermal energies for the same cluster simulated with different choices for the AMR refinement criterion.
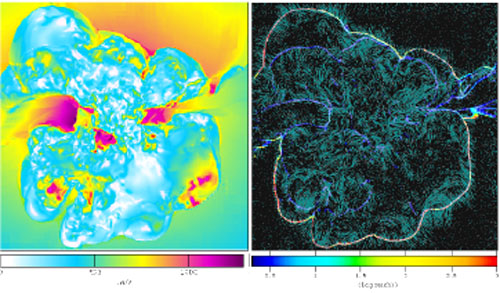 |
Figure 19. Shocks and turbulence from an Enzo AMR simulation of a galaxy cluster using a new AMR refinement criterion based on the velocity field. Left: magnitude of the gas velocity on a slice 7.5 Mpc on a side with a resolution of 18 kpc throughout the cluster. Right: map of Mach number (colors) and turbulent velocity vectors on the slice. The virialization shock and internal shocks are kept very sharp using the new refinement criterion. From [108]. |
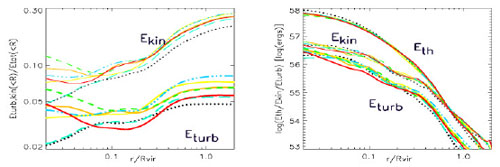 |
Figure 20. Radial profiles of turbulent kinetic, bulk kinetic, and thermal energies for the same cluster simulated with different resolutions and choices for the AMR refinement criterion. Left: as fractions of the total energy (turbulent+bulk+thermal). Right. Unnormalized profiles. From [108]. |
5.4. Origin of Cluster-Wide Magnetic Fields
There is growing evidence that the intra-cluster medium (ICM) is permeated with magnetic fields, as indicated by the detection of large-scale, diffused radio emission called radio halos and relics (see recent reviews by [99, 100]. The radio emissions are extended over 1 Mpc, covering the whole cluster. By assuming that the total energy in relativistic electrons is comparable to the magnetic energy, one often deduces that the magnetic fields in the cluster halos can reach 0.1-1.0 µG and the total magnetic energy can be as high as 1061 erg [101]. The Faraday rotation measurement (FRM), combined with the ICM density measurements, often yields cluster magnetic fields of a few to 10 µG (mostly in the cluster core region). More interestingly, it reveals that magnetic fields can have a Kolmogorov-like turbulent spectrum in the cores of clusters [102] with a peak at several kpc. Other studies have suggested that the coherence scales of magnetic fields can range from a few kpc to a few hundred kpc [92, 93, 94], implying large amounts of magnetic energy and fluxes. Understanding the origin and effects of magnetic fields in clusters is important because they play a crucial role in determining the structure of clusters through processes such as heat transport, which consequently affect the applicability of clusters as sensitive probes for cosmological parameters [103].
The simulation described above suggests a way to magnetize the ICM of a galaxy cluster. Magnetic flux deposited into the IGM at high redshift by one or more AGN could provide a seed field for subsequent turbulent amplification and mixing driven by cluster mergers. Norman & Bryan (1999) showed that cluster formation produces cluster-wide turbulence with Mach numbers ranging from 0.1 in the core to 0.3 near the virial radius. This could drive a fast dynamo, amplifying the seed field to observed levels.
To test this hypothesis Xu et al. (2009) [106] carried out a cosmological AMR MHD simulation using the ENZO+MHD code in which an AGN is switched on in a subcluster at a redshift of z = 3. Just as in the calculation described above, a magnetically-dominated jet-lobe system is formed by injecting magnetic energy for 36 Myr. Thereafter the AGN is switched off, and the magnetic fields evolve passively subject to the fluid dynamics of cluster assembly.
Fig. 21 shows images of the projected baryon density (upper row) and magnetic energy density (bottom row) for various times in the evolution of the cluster. One can see that magnetic energy, initially deposited in a small volume, is amplified and distributed throughout the cluster by the end of the simulation at z = 0.
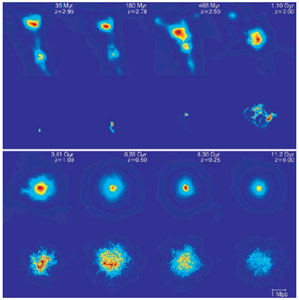 |
Figure 21. Enzo AMR MHD cosmological simulation of the magnetization of the ICM of a galaxy cluster due to a single AGN injection event at z = 3. Snapshots of projected baryon density (upper rows) and magnetic energy density (bottom rows) for different epochs of the evolving cluster. A major merger at z = 2 induces cluster turbulence which spreads and amplifies the magnetic field throughout the cluster by z = 0. This model predicts an RMS field strength which is nearly constant with radius out to a Mpc at late times. From [106]. |
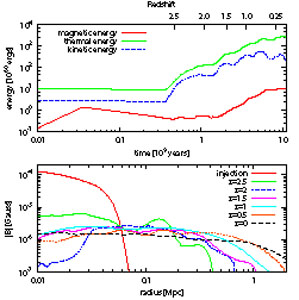
Fig. 22 shows the evolution of the magnetic field in both time and space. A total of about 2 × 1060 erg of magnetic energy is injected over 36 Myr. It then decreases due to expansion to about 1/4 that value by z = 1.5. Then it is amplified to about 1061 erg by turbulence during cluster formation. The lower panel shows how turbulent diffusion spreads the magnetic field throughout the cluster by z = 0, with an average value of about a microgauss out to a radius of 1 Mpc.
 |
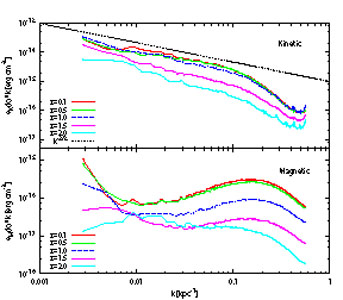 |
Figure 22. Magnetic field evolution in the simulation shown in Fig. 21. Left: Magnetic energy versus redshift, as in integrated quantity (top) and as a function of radius. Right: Evolution of the power spectra of kinetic energy (top) and magnetic energy bottom). From [106]. |
|
To see that turbulence is indeed the agent for field amplification and
spreading, the right panel of Fig. 22 shows
power spectra for gas kinetic energy and magnetic energy.
By forcing the AMR code to refine to the maximum level everywhere within
the virial radius, we have an effective uniform grid resolution of
6003 in the cluster region. We see a kinetic energy spectrum
which is consistent with the Kolmogorov self-similar scaling result over
the wavenumber range 0.01
 k
k
 0.1
kpc-1. Turbulent energy is
damped at smaller scales due to numerical dissipation, and back-reaction of
the magnetic field which is amplified the most at these scales.
0.1
kpc-1. Turbulent energy is
damped at smaller scales due to numerical dissipation, and back-reaction of
the magnetic field which is amplified the most at these scales.