3. STATISTICAL PROPERTIES OF SUPERBUBBLE POPULATIONS

The statistical properties of the superbubble populations offer another test of the standard evolutionary model for the shells. Oey & Clarke (1997) derived expressions for the differential size distribution N(R) dR of superbubbles in a uniform ISM, using the analytic expressions for adiabatic evolution (equation 1). We considered a power-law mechanical luminosity function for the parent OB associations,

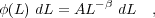(2)

with 2, which is robustly associated with the H ii region luminosity function (e.g., Kennicutt et al. 1989; Oey & Clarke 1998a). The superbubble growth is taken to be pressure-confined when the interior pressure P_i = P₀. Star formation is assumed to be coeval within each OB association, with SNe therefore exploding over a period t_e = 40 Myr, the lifetime of the lowest-mass SN progenitors. For constant star-formation rate and power-law (L), we found that:

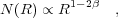(3)

effectively yielding N(R) R^-3 for = 2. Oey & Clarke (1997) also derive N(R) for other combinations of and (L).

This result agrees well with the H i shell catalog for the Small Magellanic Cloud (SMC) compiled by Staveley-Smith et al. (1997). This is by far the most complete sample of H i shells obtained for any galaxy, as evidenced by the fact that the relative number counts of H ii regions and H i shells are in excellent agreement with their relative life expectancies. For shells having R 100 pc, the fitted power-law slope = 1-2 is 2.7 ± 0.6, in excellent agreement with the general prediction of = 3.

We note that different models for ISM structure yield different predictions for N(R). For example, Stanimirovic et al. (1999) suggest a possible fractal structure for the neutral ISM. From the same H i dataset of the SMC, they find a fractal dimension implying a size distribution for H i holes of = 3.5. It is difficult to empirically differentiate this from our model, having = 3; but it is worth noting that the predictions are intrinsically different.

However, the superbubble size distribution presently is not a sensitive test in determining whether or not the objects evolve adiabatically. If all the internal energy is radiated away, the objects are predicted to follow the momentum-conserving law given by Steigman et al. (1975):

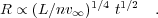(4)

The stall radius R_f in this case is only 1.3 times larger than for the adiabatic model, and the size distribution follows the same law N(R) R^1-2 (Oey & Clarke 1997). The observations of hot gas are therefore vital confirmation that the adiabatic model applies to a significant fraction of superbubbles.

We can also derive the distribution of expansion velocities N(v) dv, which describes only the growing objects (Oey & Clarke 1998b):

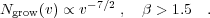(5)

This again compares well with the SMC H i shell catalog: the fitted power-law slope is 2.9 ± 1.4. Thus, despite the crude assumptions in deriving the shell size and velocity distributions, the data suggest that the neutral ISM in the SMC is fully consistent with superbubble activity dominating the structure. Although most other available H i shell catalogs are highly incomplete, preliminary results for a few other galaxies also show agreement with our model for the size distribution (Kim et al. 1999; Mashchenko et al. 1999; Oey & Clarke 1997).