It is now well established that the activity associated with both star formation and AGN increases dramatically (20× ) out to a peak at z ~ 2-3 using SFRs determined by the UV continuum, FIR and radio continuum and that beyond z = 3 there may be a gradual decline in the SFR density, although the measurements become increasingly difficult at these redshifts.
At high redshift, one might expect that the same two modes pertain, yet their relative importance could be quite altered. On the one hand, high-redshift galaxies should have higher gas mass fractions than the typical 5-10% of low-redshift spiral galaxies like the Milky Way - leading to higher rates of star formation associated with the quiescent linear mode of star formation. But at the same time, one expects a greatly elevated rate of galactic merging/interaction, increasing the frequency of the starburst mode. Which of these dominates is not at all clear without a numerical simulation to track their relative importance, keeping track of the rare and brief mergers.
8.5.1. Cosmic evolution: M* and MISM and star formation luminosities
In order to test the framework developed above against the observed
cosmic evolution of galaxies, I developed a simple Monte Carlo
simulation - including: star formation in the quiescent and
merger-driven burst modes, merging of dark matter haloes and their
contained galaxies, and accretion of fresh gas from the external
large-scale structure environment. The simulation starts at z = 6
with a population of 10 million dark matter haloes having a mass
function approximating that seen in simulations for z = 6 (e.g.,
Heitmann et al.
2010).
Each halo is started at z = 6 with
a galaxy of baryonic mass equal to the dark matter mass times the
universal baryon fraction, with 90% of the baryons being gaseous ISM and
10% stellar mass. I then let the galaxy and dark matter halo population
evolve with 50 Myr timesteps down to z = 1. At each
timestep, gas is converted to stellar mass at the quiescent SFR given by
Equation 8.29. At each timestep, haloes are
also randomly sampled for having undergone a merger with a probability
weighted as
(1 + z)2.5 Mhalo0.125
(Fakhouri & Ma
2010).
This merger rate is normalised such that 2% of
the haloes merge per 50 Myr at z = 6. The secondary galaxy
for each merger was also selected randomly from the galaxy population
weighted by (mass ratio)-2.1
(Fakhouri & Ma
2010).
For those galaxies selected to merge, the SFE was
increased by a factor of 10-50 (but only for one timestep). Gas
accretion to the galaxy halo was taken as
M = 6.6(Mhalo / 1012)1.15
(1 + z)2.25 × 0.165
(Dekel et al.
2009)
for Mhalo < 1012
M
. For
larger-mass haloes,
we assumed simply that the accretion was cut off - either by the
accretion shocks or by AGN feedback - the former is a departure from
Dekel et al. but some reduction of accretion is required in order
to have the massive objects become gas-poor ellipticals at modest
redshifts as shown observationally.
Minor non-critical details which were included were that: 1) the
effective accumulation of stellar mass was taken to be 70% of the
integrated star formation (i.e., assume 30% of the stellar mass is
recycled eventually in mass loss), 2) the accretion of external gas to
star-forming galaxy was delayed by 1 Gyr after it accreted to the
halo boundary (to account for the infall time) and 3) during starbursts,
ISM mass was shed from the galaxy at a rate equal to the SFR (only for
the burst mode). The star formation luminosity (motivated to model the
IR luminosity function) was taken very crudely as the total
luminosity from stars formed in the last 50 Myr plus that from
young stars in earlier timesteps reduced by a factor of two in each
timestep. Specifically, the luminosity associated with recent star
formation was taken to be 1010
L per
M per
year of star formation, based on observations of local galaxies.
8.5.2. Need ISM replenishment by accretion
This simplistic model was remarkably useful to explore critical aspects of the evolutionary scheme involving quiescent and burst-mode star formation with a reasonable gas accretion hypothesis. Figure 8.30 shows the evolved mass functions of stars and ISM gas and the star formation luminosity at z = 2.5 and 1. For this figure, the simulation included merging galaxies and their associated starbursts but was without accretion of gas from the environment. In this case, the ISM runs down at a rate given by local Universe star formation laws and the original gas content of the haloes is exhausted by z = 2.5 to a level much less than that seen either at z = 2 or in present-epoch galaxies.
 |
Figure 8.30. The mass and luminosity functions for galaxies at z = 2.5 (left) and z = 1 (right) derived from a Monte Carlo simulation including galaxy merging and associated starburst activity but no gas replenishment via accretion from the external environment. The dashed line is the original (z = 6) galaxy mass distribution (gas+stars). The original gas supply is exhausted far too quickly, even by z ~ 2. |
8.5.3. ULIRG starbursts account for high-L tail
The simulation shown in Fig. 8.31 includes gas
accretion as formulated above but without the starburst activity
associated with galaxy merging. Now, the ISM and stellar mass functions
exhibit characteristics similar to those observed at z = 2.5 and
1, i.e., 
50% gas
mass and 10%, respectively. However, even at z = 2.5, the star
formation luminosity function is lacking the power-law tail at the
high-luminosity end. To reproduce the power-law tail, the starburst
activity associated with galaxy merging is needed, as shown in
Fig. 8.32. (The low-mass and low-luminosity
ends of the distribution functions rise more steeply than is observed
since no effort was made to model the behaviour there - this shallow
slope is often attributed to star-formation winds driving galactic
mass-loss at velocities above the escape velocity of lower-mass galaxies.)
 |
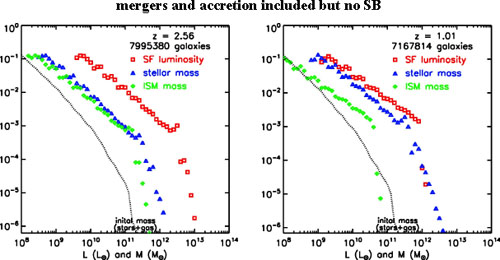Figure 8.31. Similar to
Fig. 8.30 except that gas accretion at halo masses
below 1012
M |
 |
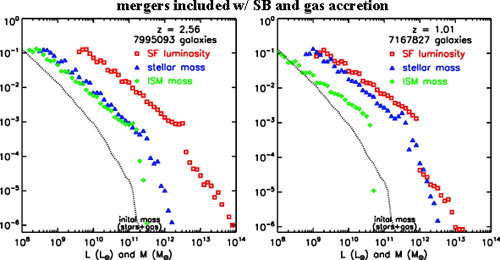Figure 8.32. Here both accretion and starburst activity during galaxy merging are included, giving a reasonable qualitative match to the observed high-end mass and luminosity functions. |