Annu. Rev. Astron. Astrophys. 2013. 51: 207-268 Copyright © 2013 by Annual Reviews. All rights reserved

9. CONCLUSIONS AND OPEN PROBLEMS

We have summarized the efforts to measure X_CO in the Milky Way and other galaxies, as well as the theoretical arguments and studies that show that CO can be used as a tracer of molecular mass, under certain conditions, through the adoption of a CO-to-H₂ conversion factor.

In the following paragraphs, we would like to offer concise answers to a few key questions that have been developed elsewhere in this review:

• What is the "best" value for the Milky Way X_CO?
• Under what circumstances is the assumption of "Galactic X_CO" likely to be good or bad?
• How well can we calibrate X_CO as a function of metallicity?
• What is the most appropriate value of X_CO in ULIRGs?
• What can we say about X_CO in the distant universe?
• Can we offer a practical prescription for X_CO based on observables?
• What observations and calculations are necessary to move forward?

Measurements in the Milky Way have achieved a very good level of sophistication and consistency, beyond what is possible in external galaxies. We have shown that there is an assuring degree of uniformity among the large scale values of X_CO obtained through different techniques, particularly in the inner disk (1 kpc R 9 kpc). We recommend adoption of a constant X_CO = 2 × 10²⁰ cm^-2(K km s^-1)^-1 (_CO = 4.3 M (K km s^-1 pc²)^-1) with an uncertainty of ± 0.1 dex (a factor of 1.3) for the inner disk of the Milky Way. The evidence for a large scale Galactic X_CO gradient and its magnitude are, presently, at best unclear, and the simplicity of a constant conversion factor is preferable. Nonetheless, there is convincing evidence that X_CO in the Milky Way center region is smaller than in the disk by factors of 3-10, and this is reaffirmed by extragalactic observations that find that a low X_CO is not uncommon in other galaxy centers. Following the results obtained by a number of studies, we recommend using X_CO 0.5 × 10²⁰ cm^-2(K km s^-1)^-1 for R 500 pc in the Milky Way. The uncertainty is difficult to quantify, but taking the different measurements obtained as well as the results discussed for galaxy centers and starbursts, we recommend ± 0.3 dex (a factor of 2). We expect that further CO multitransition modeling, -ray, and dust continuum studies will help constrain better this value as well as that of a possible large scale Galactic gradient. For the outer Milky Way we expect X_CO to increase, in principle, following the same physics underlying its increase in low metallicity environments, as we discuss below.

It is important to recognize that these are average numbers, strictly valid for GMCs on scales of tens of pc. The validity of invoking anything like a constant X_CO on a line-of-sight by line-of-sight basis is considerably less defined. Both theoretically and observationally, we have shown that considerable variation can exist on small scales, reflecting local chemistry and physical conditions.

The most mature techniques in "normal" galaxies remain virial mass measurements and the use of dust as an optically thin tracer. Both techniques have their drawbacks, and we particularly emphasize the ambiguous (at best) sensitivity of virial mass measurements to any extended envelope of H₂ mixed primarily with C⁺ rather than CO. At solar metallicities, a wide range of measurements yield X_CO,20 1-4, but with large (still factor of 2) scatter and uncertainties related to the dynamical state of clouds and the environmental dependence of dust properties. In the absence of further characterization or studies, we recommend the conservative approach of adopting X_CO = 2 × 10²⁰ cm^-2(K km s^-1)^-1 with an uncertainty of ± 0.3 dex (a factor of 2) in the disks of normal, solar metallicity galaxies. This applies to galaxies where the CO emission is dominated by self-gravitating H₂ clouds or cloud complexes. This value can approximately be applied down to metallicities ~ 0.5 Z, and in regions where the total gas plus stars surface density is 300 M pc^-2. ALMA will greatly expand the application of both dust and virial mass techniques. Other future prospects will include modeling of resolved [CII] emission, now widely available thanks to Herschel, the extension of spectral line modeling beyond bright galaxy centers, and further exploitation of galaxy scaling relations.

Several regimes exhibit clear departures from a Galactic X_CO. Some, but not all galaxy centers share a value of X_CO lower than disks, qualitatively similar to that observed in overwhelmingly molecular massive starburst galaxies such as ULIRGs. Dust and spectral line modeling of these central regions show depressed X_CO compared to galaxy disks, with the depression spanning a wide range of X_CO up to an order of magnitude below Galactic. These central X_CO depressions are not universal, although they seem correlated with the stellar surface density _* (Sandstrom et al. 2012), and additional information appears necessary to predict the appropriate X_CO for use in any specific galaxy center.

A wide variety of evidence points to high X_CO in low metallicity regions: the absolute and normalized faintness of CO, high [CII]-to-CO ratios, high SFR-to-CO ratios, large dust-based X_CO determinations, and theoretical calculations of cloud structure. Virial masses represent a significant exception to this body of evidence. When derived at high spatial resolution, these tend to show little or no enhancement in X_CO above the Galactic value, even in low metallicity systems. We review the theoretical expectations for the shrinking of the opaque CO emitting surface relative to H₂ as metallicity decreases. We favor a self-consistent use of dust, an optically thin tracer of gas, as the currently most mature methodology to robustly estimate molecular mass at low metallicity. We also highlight the problems with the blind use of a dust-to-gas to metallicity calibration. The present self-consistent dust-based X_CO estimates offer support for the picture of rapidly increasing X_CO at low metallicity, but still yield a wide range of X_CO even for similar techniques applied to the same galaxy. We recommend adopting a shielding-based prescription such as that presented by Wolfire, Hollenbach & McKee (2010) or Glover & Mac Low (2011) to account for the effects of metallicity, with the normalization chosen to match a "Galactic" X_CO at solar metallicity.

The uncertainties involved in any metallicity-dependent correction remain substantial. As a first order picture, we expect X_CO will change slowly for metallicities larger than 12 + log[O/H] ~ 8.4 (approximately Z / 2), and considerably faster at lower metallicities. By the time X_CO reaches 10 times the Galactic value the CO emitting surface encompasses only ~ 5-10% of the H₂ cloud, suggesting that the utility of CO as a global tracer of H₂ will become more and more marginal as one moves to progressively metal-poorer environments. Rather, CO will in fact be a tracer of high column density peaks and well-shielded regions.

There is general agreement that the processes operating in overwhelmingly molecular and turbulent starbursts, where high gas temperatures are also present, drive X_CO to values that can be substantially lower than in solar metallicity galactic disks. Because of the role of velocity dispersion in setting X_CO, in the absence of a self-regulating mechanism it is almost certain that there exists a continuum of values rather than a unique X_CO value that is applicable in all cases. The typical result of the one-component modeling is X_CO ~ 0.4 × 10²⁰ cm^-2(K km s^-1)^-1 for massive, turbulent, ultraluminous starbursts. The range around this value is large, at least ± 0.5 dex, most of it likely representing real physical variation among sources.

The picture of X_CO at high-redshift is still emerging, and instruments like ALMA will make a crucial contribution to better understand it. Lacking direct measurements, the best approach is to use knowledge of the physical drivers of X_CO developed in local galaxies, as well as scaling and consistency arguments. The simplest approach is to identify the brightest, off-main sequence massive SMGs likely due to starbursting mergers with local ULIRGs, while disky, rotation-dominated "main sequence" galaxies are to first order more likely similar to local disks dominated by self-gravitating or virialized molecular clouds. This is an area of active research. The picture will become more nuanced as new observations revealing the resolved kinematics of the molecular gas and its excitation are obtained. In particular, observations of "main sequence" galaxies at z ~ 1-2 suggests that metallicity effects will become an increasingly important consideration at high-z, as observations push to lower galaxy masses at higher redshifts and consequently more metal-poor environments (Genzel et al. 2012).

9.1. Toward a Single Prescription

Ultimately, we desire a prediction for X_CO based on observable properties, for objects ranging from low-metallicity dwarf galaxies to high surface-density ULIRGs. In the following paragraphs we present some steps in that direction, referring to _CO since that is the quantity most often useful for distant galaxies.

Based on the discussions in Section 6.1 and Section 7, _CO can be thought of as having two primary dependencies; one related to the temperature and velocity dispersion effects driving a low value in ULIRGs, the other related to the dominance of CO-faint molecular gas driving a high value at low metallicities. Treating the two effects as separable, _CO = _CO,MW f_COF f_SB, where _CO,MW represents an overall normalization under Milky Way disk conditions. The factor f_COF corresponds to a correction that accounts for the fraction of H₂ mass associated with the outer layers of clouds where most CO is photodissociated. The factor f_SB accounts for changes in _CO due to temperature and velocity dispersion.

Drawing from Section 6.1, f_COF may be approximated by considering Eq. 27 applied to a population of identical, fixed surface density clouds,

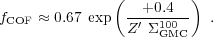(30)

Here we assume that dust-to-gas ratio tracks metallicity, Z' is the metallicity normalized to the solar value, and _GMC¹⁰⁰ is the average surface density of molecular clouds in units of 100 M pc^-2.

The factor f_SB is considerably more tentative. The simple theoretical arguments we outline in Section 2, as well as simulations (e.g., Shetty et al. 2011), suggest that both the gas velocity dispersion and temperature are key parameters. Nonetheless, keep in mind that the fundamental driver of X_CO is what fraction of the CO luminosity arises from gas in self-gravitating clouds, versus an extended not self-gravitating component bound by the total mass of the system. Given current observational constraints and our desire to parametrize in terms of measurable quantities, we suggest that the variations between normal disks, galaxy centers, and ULIRGs are mostly captured by a surface density-dependent factor of the form f_{SB total}^-, where _total refers to the combined gas plus stellar surface density on kpc scales.

Present constraints remain scarce, but we make an effort to present them in Fig. 12. The data corresponds to the kpc-scale dust-based measurements in nearby disks by Sandstrom et al. (2012), as well as the overlap between the ULIRG samples by (from which we take dynamical masses and _CO, Downes & Solomon 1998) and (from which we take _CO estimates, Papadopoulos et al. 2012). In this latter case, _CO is derived from one-component (similar to the results by Downes & Solomon 1998) or two-component multi-transition fits (which include contributions from a dense phase). The dynamical surface density is dominated by the stellar component, even in ULIRGs (Downes & Solomon 1998). Informed by the theoretical arguments leading to Eq. 16, and by the results of detailed modeling (Shetty et al. 2011), we plot _{CO total}^-0.5 normalizing to our recommended Galactic _CO value at _total = 100 M pc^-2. Obviously this correction should not extend to surface densities below those of resolved self-gravitating GMCs.

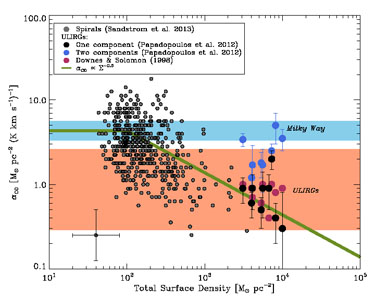Figure 12. Conversion factor as a function of total surface density for nearby disk galaxies and ULIRGs. The gray points illustrate the high S/N solutions for CO based on dust emission on kpc scales in a sample of nearby disks, with typical errors illustrated in the lower left corner (Sandstrom et al. 2012). The corresponding surface densities are dominated by the stellar component. For the ULIRGs we plot the CO determinations by Downes & Solomon (1998, magenta) and Papadopoulos et al. (2012, multitransition one-component fits in black and two-component fits in blue, error bars represent possible range). The abcisa is from the dynamical mass measurements by Downes & Solomon (1998), thus we plot only the overlap of both samples. The color bands illustrate the recommended ranges for Milky Way and ULIRG conversion factors. The -0.5 line for > 100 M pc-2 is a reasonable representation of the overall trends when considering the one-component fits.

Given the large uncertainties and the small dynamic range of the _CO measurements this simple prescription seems to reproduce the trends present in the data reasonably well, particularly for the results of one-component models for the ULIRGs (which we consider most mature). The observations may be fit with a smaller although with considerable uncertainty (e.g., Sandstrom et al. 2012), which leads us to prefer the theoretically motivated 0.5. Density increases in the self-gravitating molecular material with respect to the Milky Way average GMC properties will drive the _CO points up, while increases in temperature will drive them down. The sample spans a factor of ~ 2 in T_dust, which should be a reasonable proxy for gas temperature in the ULIRGs. Although we have searched for the signature of temperature effects in the data, we see no discernible correlation with T_dust (e.g., Magnelli et al. 2012). Likely, the sample lacks the necessary dynamic range to pull those effects out of the data. Possibly, as previously discussed, the lack of a temperature correlation could be in part due to cancelations between the opposite effects the density of self-gravitating clouds and their temperature have on X_CO. Thus, as a tentative first step for a simple conversion factor prescription, we suggest using

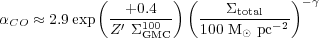(31)

in M (K km s^-1 pc²)^-1, with 0.5 for _total > 100 M pc^-2 and = 0 otherwise. Note that we still expect a fair dispersion around this average prescription, representing the variation in local parameters such as temperature or _GMC.

There has been an exciting range of theoretical and numerical developments on calculations of X_CO in the last few years. The coupling of high resolution hydrodynamical simulations including chemistry and radiative transfer, with increasingly sophisticated theoretical modeling of photodissociation regions and molecular clouds, and galaxy scale simulations offers an exciting avenue of progress. Numerically derived calibrations, such as those obtained on small scales by Glover & Mac Low (2011) or Shetty et al. (2011) and on large scales by Narayanan et al. (2012), show much promise. Such simulations are likely to become increasingly reliable as the modeling is able to better incorporate and couple the physics, kinematics, and radiative transfer on the small and large scales. Grounded on observations, simulations may offer the ultimate way to calibrate the CO-to-H₂ conversion factor in a variety of environments.

We especially thank the following people for providing extensive comments on earlier versions of this manuscript: Leo Blitz, Ewine van Dishoeck, Neal Evans, Reinhard Genzel, Erik Rosolowsky, and Nick Scoville. We also thank the following people for providing figures, comments, advise, and/or for enduring one of the partial or complete drafts of this manuscript: Jean-Philippe Bernard, Chris Carilli, Thomas Dame, Jennifer Donovan Meyer, Isabelle Grenier, Andrew Harris, Remy Indebetouw, Frank Israel, Guölaugur Jóhannesson, Douglas Marshall, Desika Narayanan, Eve Ostriker, Padelis Papadopoulos, Jorge Pineda, Karin Sandstrom, Rahul Shetty, Andrew Strong, Linda Tacconi, Stuart Vogel, Fabian Walter, and Zhi-Yu Zhang. A.D.B. wishes to acknowledge partial support from a CAREER grant NSF-AST0955836, NSF-AST1139998, and from a Research Corporation for Science Advancement Cottrell Scholar award, as well as full support from his wife, Liliana.