2. THE INITIAL CONDITIONS

Nowadays it is pretty common to find in the literature studies of the formation and evolution of galaxies in a cosmological context, meaning that initial conditions consist of a scale-free or nearly scale-free spectrum of Gaussian fluctuations as predicted by cosmic inflation and with cosmological parameters determined from observations of the cosmic microwave background radiation obtained by spacecrafts such as WMAP [275, 123]. However, the most detailed and sophisticated cosmological simulations to date, such as the Millennium-II simulation [30] and the Bolshoi simulation [119] have force resolutions of the order of 1 kpc. This is barely enough to resolve large galaxies, but it is clearly insufficient to solve in detail DGs, whose optical radii are some times smaller than that. A lot in resolution can be gained by zooming in and re-simulating small chunks of a large cosmological box [284, 61, 286]. This method is gaining pace and has been applied by various groups to DGs [169, 245, 213]. Still, at the present time the best way to accurately simulate a DG is by numerically studying it as a single isolated entity [180, 287, 233, 252, 256, 306].

Numerical studies of galaxies in isolation assume some initial configuration of gas density, temperature and stellar distribution. This initial configuration is an equilibrium status of the system. Starting from an equilibrium condition is clearly necessary in order to pin down the effect of perturbing phenomena (star formation, environmental effects, AGN feedback, and so on).

A common strategy is to consider a rotating, isothermal gas in equilibrium with the potential generated by a fixed distribution of stars and/or of dark matter [315, 261, 159]. Rotating gas configurations are usually better described by means of a cylindrical coordinate system (R, ϕ, z). Often, axial symmetry is assumed. The relevant equation to solve in order to find the density distribution of gas (R, z) is thus the steady-state (time independent) Euler equation

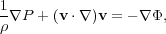(1)

where P is the pressure, v is the bulk velocity of the gas and is the total gravitational potential. In this equation, only the component v_ϕ of the velocity must be considered because it gives centrifugal support against the gravity. Eq. 1 in fact implies that the gravitational pull is counter-balanced by the combined effect of pressure gradient and centrifugal force.

Most of the authors assume to be independent of . This means that the self-gravity of the gas is not considered. A typical justification of this choice is "The omission of self-gravity is reasonable, given that the baryonic-to-dark matter ratio of the systems is ~ 0.1." [79]. However, even if the total mass of a DG is dominated by a dark matter halo, within the Holmberg radius (the radius at which the surface brightness is 26.5 mag arcsec^-2), most of the galaxy is made of baryons [206, 297], so the inclusion of gas self-gravity in the central part of a DG appears to be important. I will come back to this point later in this section. For the moment it is enough to take note of the fact that the assumption that is independent of greatly simplifies the calculation of the steady-state density configuration. Furtermore, a barotropic equation of state P = P() and a dependence of the azimuthal velocity v_ϕ with known quantities is commonly assumed.

A widely used strategy is to assume that v_ϕ = ev_circ, where v_circ = √R d / dR is the circular velocity and e is the spin parameter that determines how much the galaxy is supported against gravity by rotation and how much it is supported by the pressure gradient. A typical value for e is 0.9, independent on the height z [314, 295]. [293] assume that e = 0.9 in the plane of the galaxy, but it drops exponentially with height in order to have non-rotating gas halos. It is however important to remark that, according to the Poincare'-Wavre theorem [147, 302, 13], the rotation velocity of any barotropic gas configuration (including thus also isothermal configurations) in rotating equilibrium must be independent of z. In other words, it is possible to construct a centrifugal potential to add to in Eq. 1 only if the circular velocity is independent on z.

Other authors [58] solve instead the equilibrium equation in the plane:

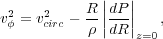(2)

and assume the azimuthal velocity to be independent of z, in compliance with the Poincare'-Wavre theorem. The density at any z is then found integrating the z-component of the hydrostatic equilibrium equation, for any R. Some authors then [109, 67, 306] set the gas in rotation around the z-axis, using the average angular momentum profile computed from cosmological simulations [37].

A different approach is followed by [7]. Initially, there is no balance between gravity and pressure and the gas collapses into the midplane. Supernovae (SNe) go off, principally along the disk and this drives the collapsed gas upwards again. Eventually, upward and downward flowing gas come into dynamical equilibrium. Some multi-phase simulations [94, 155] adopt a similar approach for the diffuse component, i.e. the distribution of diffuse gas starts far from equilibrium. Then, it relaxes on a few dynamical time scales to a quasi-equilibrium state, which represents the initial conditions for the simulation.

One should be aware of the limitations of an equilibrium model without gas self-gravity. Most of the numerical simulations treat self-consistently the process of star formation. Since star formation occurs when the gas self-gravity prevails over pressure, neglecting the gas self-gravity in the set up of the model is clearly inconsistent. Moreover, without self-gravity, there is the risk of building gas configurations which would have never been realized if self-gravity were taken into account. In order to solve these problems, Vorobyov et al. [331] explicitly took into account gas self-gravity to build initial equilibrium configurations. The gravitational potential is composed of two parts, one is due to a fixed component (dark matter and eventually also old stars), one (_g) is due to the gas self-gravity. The gas gravitational potential _g is obtained by means of the Poisson equation

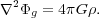(3)

The gas density distribution is thus used to calculate the potential, but this potential is then included in the Euler equation to find the gas distribution. Clearly, an iterative procedure, analogous to the classical self-consistent field method [200], is necessary to converge to an equilibrium solution.

For a given mass M_DM of the dark matter halo, many solutions are possible, according to the initial assumption about the density distribution of the gas. However, the self-gravitating equilibrium configurations always have a maximum allowed gas mass M_max, unlike the case of non-self-gravitating equilibria which can realize configurations with unphysically high gas masses. Moreover, only for some of the solutions, star formation was found to be permissible by Vorobyov et al. (two star formation criteria based on the surface gas density and on the Toomre parameter were assumed). The minimum gas mass M_g^min required to satisfy the star formation criteria was found to be mainly dependent on the gas temperature T_g, gas spin parameter e and degree of non-thermal support. M_g^min was then compared with M_b, the amount of baryonic matter (for a given M_DM) predicted by the CDM theory of structure formation. Galaxies with M_DM 10⁹ M are characterised by M_g^min M_b, implying that star formation in such objects is surely possible as the required gas mass is consistent with what is available according to the CDM theory. On the other hand, models with M_DM 10⁹ M are often characterised by M_g^min ≫ M_b, implying that they need much more gas than available to achieve a state in which star formation is allowed. In the framework of the CDM theory, this implies the existence of a critical dark matter halo mass below which the likelihood of star formation drops significantly ([331], see also [347, 208, 263]).