7. THE MECHANICAL FEEDBACK

Explosions of SNe (of both Type Ia and II) and stellar winds are the main drivers of the ISM dynamics, at least in DGs (in larger galaxies, AGNs might play a fundamental role). Unfortunately, for the foreseeable future, galactic-scale simulations will not be able to solve individual SN remnants or the effect of the wind from individual stars. Hence, heuristic, sub-grid recipes are needed to treat the mechanical feedback. This is a complex and still active research field. Although feedback prescriptions have been found to address specific issues [89, 54], no recipe appears to be widely applicable and physically justifiable. Comparison studies have been performed [300, 249, 116], and the overall conclusion (see in particular the Aquila comparison project, [249]) is that the outcomes of numerical simulations crucially depend on the feedback prescriptions and none of the considered codes is able to satisfactorily reproduce the observed properties of the baryonic component of galaxies.

Broadly speaking, feedback schemes can be divided into two categories: kinetic feedback [3, 283, 52] and thermal feedback [288, 230, 191, 269]. Kinetic feedback schemes are mostly used in SPH simulations (but see [67]). The SN explosion energy is transformed into kinetic energy of neighbouring particles. A kick is given to a few neighbouring particles, which move after the kick with a prescribed velocity, along a random direction. The problem with this scheme is that it is not physically justifiable and it is not easy to create galactic winds, unless kick velocities are chosen along prescribed directions.

In thermal feedback schemes instead, the SN energy is used up to heat the ISM. A well-known drawback of this scheme is that the cooling timescale of the particles affected by this thermal feedback is typically very short (often shorter than the timesteps of the simulation). The input energy is thus radiated away before it can be converted to kinetic energy. This leads to the so-called overvcooling problem [111]. Various authors have tried to remedy to this problem by simply switching off the cooling [274, 288, 230]. The inefficiency of thermal feedback is usually attributed to poor spatial resolution: the energy is deposited in gas that is too dense, because the hot, low-density, bubbles that fill much of the volume of the multi-phase ISM are missing. In fact, in models in which the multi-phase description of the ISM is taken into account a decoupling of the different thermal phases can be realized (some times arbitrarily) and the overcooling problem can be avoided [248, 195].

Another possibility to overcome the overcooling problem is the use of radiative feedback schemes [101]. Eventually, also cosmic rays have been suggested as an additional source of feedback [106, 65, 26]. Also a correct inclusion of stellar dynamics can be a way to avoid the overcooling problem (see Sect. 3). A much broader discussion would deserve the description of the feedback from the central AGN. This kind of feedback has gained popularity in the last decade. It appears in fact to be a useful recipe to use in semi-analytical models of structure formation [51]. However, it is not clear how significant the AGN feedback can be for the evolution of low-mass galaxies. Scaling relations [77, 181] indicate that DGs possess very small central massive black holes. It is very likely that all these forms of feedback occur in real galaxies. However, before implementing them in simulations, one should be confident that the underlying physics is well understood and that reasonable parametrisations can be used.

Although feedback schemes are widely debated in the literature, less problematic appears to be the amount of energy a SN explosion deposits into the ISM. A value of 10⁵¹ erg is assumed as it represents the typical SN explosion energy E_SN [293, 53]. It is however worth reminding that SN kinetic explosion energies (theoretically calculated or deduced from observations) cover a very broad range, from a few 10⁴⁸ ergs of the faintest SNe to the 10⁵² ergs or more of the hypernovae [199].

Some authors adopt a thermalization efficiency є_SN, in order to account for the radiative energy losses during the early phases of the evolution of a SN remnant. A commonly adopted value of є_SN is 0.1 [243]. Indeed, the simulations of Thornton et al. [310] suggest that only ~ 10% of the SN explosion energy can be used up to thermalize the ISM. However, detailed simulations of the impact of isolated stars on the ISM [81, 127, 96] show that the energy transfer efficiency can be even lower than 1%. A different approach, where the contribution of a whole population of stars is considered [183] clearly shows that є_SN must be a function of time. During the early phases of galactic evolution, the SN remnants expand in a very dense and cold ISM. SN remnants evolve in isolation and radiative losses are very large. Only a small fraction of the SN explosion energy goes to increase the thermal budget of the ISM. When the ISM becomes hotter and more porous, radiative losses are less significant. Various SN remnants quickly coalesce and form a superbubble. Within this superbubble, the sound speed is large. If a SN explodes inside the superbubble, the time it takes for the SN shock velocity to become equal to the sound speed is very short. This is the time at which the shock loses its identity and the energy of the SN remnant can be transfered to the ISM. Clearly, in this situation the SN remnant does not have time to radiate away a large fraction its energy, which can be thus efficiently converted into thermal energy of the ISM once the SN shock velocity becomes equal to the local sound speed.

Simple analytical estimates of the thermalization efficiency as a function of the ambient density and temperature are possible [146, 279, 31, 226, 292]. Again, these formulae show that є_SN is strongly reduced if the ambient density is large and the temperature is low. A more quantitative evaluation of є_SN for a single, isolated galaxy can be obtained as follows. The stalling radius R_s is defined as the radius at which the expansion velocity of the SN shock equals the local sound speed. At this radius, the material inside the SN shock can be causally connected with the external ISM and a transfer of energy can occur. R_s can be evaluated as [47]:

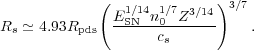(8)

Here, the SN explosion energy is expressed in units of 10⁵¹ ergs, the ambient density n₀ in cm^-3, the metallicity Z in units of the solar metallicity and the sound speed c_s in units of 10⁶ cm s^-1. R_pds is the radius of the SN shock at the moment in which cooling becomes important. Assuming that most of the SN energy at this stage is in the form of kinetic energy of the shell the energy available to thermalize the ISM is:

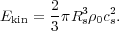(9)

The thermalization efficiency is now simply the ratio between this residual energy and the initial explosion energy E_SN. Using the value of R_pds given by [47], one obtains:

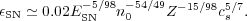(10)

This calculation is surely approximate. In particular, the ISM porosity and the possibility that various SN remnants merge have not been taken into account. However, additional corrections could be included and a more physically motivated description of the thermalization efficiency, depending on the local thermodynamical conditions, could be obtained.

Eventually, the expansion of ionisation fronts could be taken into account, as well. Simple formulae could be devised to describe the variation of the Strömgren radius surrounding a single massive star or an association of stars [280, 143]. Within this radius the cooling is indeed strongly suppressed because Ly continuum photons are used up on the spot to ionise hydrogen atoms and only photons from the Balmer series onwards can leave the H II region. Combining these formulae with the formulae describing the evolution of SN shocks and winds from massive stars seems to be theoretically possible. This method is perhaps a viable solution of the overcooling problem. Of course, once radiative hydrodynamical codes will have enough resolution to solve individual H II regions and SNeII remnants, these analytical considerations will be superfluous. However, this seems not to be possible in the foreseeable future.

To finish this section, it is important to remind that the rate of energy release from SNe and stellar winds is as important in galaxy simulations as the way this energy is converted into ISM energy. It is commonly assumed that all the stars with masses larger than a certain threshold mass m_thr explode as SNeII at the end of their lifetimes. This assumption, together with prescribed stellar lifetime functions, makes the calculation of SNII rates quite straightforward. Two sources of uncertainty must be outlined. One is the stellar lifetime function, which is still quite uncertain and model-dependent. Romano et al. [238] demonstrated however that uncertainties in the lifetimes of massive stars are not so significant and do not crucially affect the results of galaxy evolution models. More critical is the choice of m_thr. A commonly adopted value is 8 M but, since there is still not much known about the fate of stars in the mass interval [8:12] M, m_thr could be as high as 12 M. For a Salpeter IMF extending until 100 M, ~ 78 % more SNeII go off if m_thr = 8 M instead of m_thr = 12 M. Clearly, this is a non-negligible fraction.

Even more uncertain and less standardised are the feedback recipes from stellar winds and Type Ia SNe (SNeIa). Many authors even neglect these energy contributions. However, the energetic input of stellar winds is very important to establish self-regulation in the star formation process (Köppen et al. [124], see also Sect. 4). Many authors take into account stellar winds, either adopting suitable parametrisations based on observations [307], or adopting the results of models such as Starburst99 [148], which give the mechanical energy from stellar winds released by a single stellar population or due to a continuous episode of star formation. This approach has been followed, for instance, by [293, 230]. Since the stellar wind luminosity decreases with metallicity [142, 139], neglecting stellar winds is perhaps acceptable in simulations of very metal-poor DGs.

Type Ia SNe play a very important role in the evolution of galaxies, as they are the major contributors of iron, a widely used metallicity proxy [174]. Since the lifetime of SNeIa progenitors can be as long as many Gyrs [335], they represent a source of energy more evenly distributed in time than SNeII. The relevance of SNeIa for the dynamical evolution of galaxies has been shown for instance by Recchi & Hensler [222]. Many papers neglect the contribution of SNeIa as they are interested in the early evolution of galaxies and SNeIa are not assumed to occur on short timescales [159]. However, evidence is mounting [177, 250, 163, 178] that a significant fraction of SNeIa explode on timescales shorter than 100 Myr. Thus, SNeIa should be considered in chemo-dynamical models even if the time-span of the simulation is of the order of 100 Myr.

A convenient parametrisation of the SNeIa rate is [240, 90]:

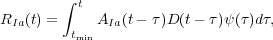(11)

where t_min is a suitably chosen minimum timescale for the occurrence of SNeIa (typically 30 Myr), A_Ia is a normalisation constant and D is the so-called delay time distribution (DTD), i.e. the distribution of time intervals between the birth of the progenitor system (usually a binary system made of two intermediate-mass stars) and the SNIa explosion. According to Eq. 11, the DTD is thus proportional to the SNIa rate following an instantaneous burst of star formation. Unfortunately, the form of the DTD is still very uncertain, although some observations [319, 164] suggest the DTD to be inversely proportional to the elapsed time, i.e. D (t) t^-1. Studies of the chemical evolution of galaxies have been performed [176, 178, 24], showing that the adoption of different DTDs drastically changes the outcome of the simulations. It is not difficult to imagine that even more drastic differences could be obtained in chemo-dynamical simulations of galaxies. The role of various DTDs on the evolution of galaxies is another aspect that has been barely considered so far in chemo-dynamical simulations and that, perhaps, deserves more attention.