The large majority of disk galaxies manifest beautiful spiral patterns of some form or other. The patterns are sometimes quite coherent and symmetric, which are described as "grand design" spirals, or the overall pattern can have little clear symmetry with individual pieces of spiral arm being hard to trace over long distances because they bifurcate or fade. The more coherent patterns are often seen in galaxies that are barred or have recently suffered a tidal interaction with a passing companion galaxy (Kormendy & Norman 1979; Kendall et al. 2011). However, the ubiquity of the spiral phenomenon, and the fact that similar patterns develop in simulations of stellar disks even when the influences of bars and companions are excluded (Sellwood & Carlberg 1984; Roskar et al. 2008a; Fujii et al. 2011; Wada et al. 2011), suggest that spirals in galaxies can also be self-excited.
Spirals are important to secular evolution because they transport angular momentum to a limited extent (see Section 3.5), scatter stars at Lindblad resonances, which increases random motion, cause radial mixing, and smooth rotation curves. I discuss each of these processes in turn.
The precise mechanism that causes spiral patterns to develop is not fully understood and a thorough survey of the various ideas would require too long a digression here (see Sellwood 2013a for a recent review). There is general agreement among theorists that spirals are gravitationally driven density waves in the stellar disk, for which there is substantial body of supporting observational evidence, both photometric (Schweizer 1976; Gnedin et al. 1996; Grosbøl et al. 2004; Zibetti et al. 2009) and kinematic (Visser 1978; Chemin et al. 2006; Shetty et al. 2007). While the idea that spiral patterns could be long-lived, or quasisteady, features has been advocated for some time (e.g. Bertin & Lin 1996), it seems increasingly certain that an individual spiral pattern does not persist for more than a few disk rotations (Sellwood 2011). The supporting evidence has to be indirect, since we cannot observe the time evolution of real galaxies, and is based on the behavior in simulations, which has not changed as their quality has improved, and is supported by the arguments developed below that disk evolution makes more sense when spirals are short-lived.
Most simulations manifest spiral patterns whose appearance changes on time scales of less than one rotation of the disk. However, power spectrum analysis (Sellwood 1989a) showed that the extreme variability of the spirals reported by Sellwood & Carlberg 1984 was caused by the superposition of a few underlying longer-lived waves, as has subsequently been found by others (e.g. Roskar et al. 2012; Grand et al. 2012; Minchev et al. 2012a).
Wada et al. (2011), Grand et al. (2012), Baba et al. (2013), and Roca-Fàbrega et al. (2013) reported that spirals in their simulations are almost material features that wind up over time according to the local shear rate of the disk. This behavior could also result from the superposition of multiple waves, as illustrated in Fig. 3 which shows the visual appearance of the combined density of two separate fixed-amplitude waves that rotate at different angular frequencies. As long as the inner wave has the higher angular speed, the combined density has most of the properties reported by these authors.
 |
Figure 3. Contours of the combined positive overdensity that results from the superposition of two open spiral patterns that each has constant amplitude and rotates at a steady, but different, rate. This is purely a set of drawings, with no underlying dynamics. The numbered sequence illustrates one full beat period, and is shown in a frame that rotates such that the outer wave does not appear to move. Notice that the largest net overdensities occur when the spiral is moderately wrapped. An animation is available at http://www.physics.rutgers.edu/~sellwood/spirals.html |
The title of this section contains the word "modes" to distinguish what is meant from the "transient spiral" illustrated in Fig. 2, which shows the time evolution of the vigorous disk response to a particularly provoking peturbation. That transient response is neither an instability, because it does not grow indefinitely, nor a mode, because it does not have a fixed shape. A mode, by contrast, is a standing wave oscillation of the system having a constant shape and frequency.
A few authors have risen to the challenge of solving for the normal modes of a smooth stellar disk with random motion. They found vigorously unstable bar-forming (Kalnajs 1972, Kalnajs 1978; Jalali 2007) and lop-sided (Zang 1976, Evans & Read 1998) modes. However, when these instabilities are avoided, perhaps by embedding the disk in a halo (see Section 5.2), studies of smooth disks generally do not reveal milder spiral modes (Toomre 1981). An exception was the study by Bertin et al. (1989), who found slowly-growing bi-symmetric spiral modes in low-mass, cool disks. But Sellwood (2011) showed that their adopted disk models would not survive, since they were subject to more vigorous multiarm instabilities that caused the background state of the disk to heat quickly. Thus these normal mode analyses have been useful to understand global disk stability, but have not yielded any promising spiral-causing modes.
However, the waves that underlie the rapidly changing patterns in the snapshots and movies from simulations do appear to be genuine modes of the disk. Each has a fixed shape and well-defined pattern speed, and grows and decays on timescales of a few disk rotations. As they are not truly long-lived, they are best described as "transient spiral modes."
Each spiral mode in the simulations is a vigorously growing instability that saturates at an overdensity of some 20% – 30% relative to the local unperturbed disk density. After it saturates it fades just about as quickly as it grew, with all the wave action that had been extracted from the particles during its growth being carried radially away from corotation at the group velocity (Toomre 1969). Wave action is finally absorbed at the Lindblad resonances (Section 2.8), where wave-particle interactions occur (Lynden-Bell & Kalnajs 1972; Mark 1974). The changes to the underlying disk caused by the scattering of stars at these Lindblad resonances seed conditions for a new instability to develop (Sellwood 2012), and thus the cycle recurs. These instabilities were missed by the authors of the above-cited stability analyses because they studied the modes of an assumed smooth, featureless disk. Sellwood (2010) found some evidence in the velocities of stars in the solar neighborhood to support this picture.
D'Onghia et al. (2013) introduced a collection of heavy, co-orbiting particles into their large-N simulations of low-mass disks, which seeded spiral responses. In one experiment, they introduced a single heavy perturber and removed it again after some evolution; they found that spiral activity continued, which they attributed to additional responses to the fluctuations caused by responses to the earlier forcing particle, in a bootstrap fashion, that they described as "nonlinear" effects, although it was unclear that the behavior they observed depended in any way on the amplitudes of the disturbances. It is also possible to regard their result as the superposition of multiple spiral modes of the underlying disk, which were triggered at moderate amplitude by the original perturbing heavy particle. Whatever the correct explanation, they concurred with Sellwood (2012) that spiral activity at one instant is directly influenced by the immediately preceding activity.
In the absence of dissipation, the recurring spirals drive up the level of random motion in the disk (see Section 3.2.2). As Q rises, the disk becomes ever less able to support collective oscillations, and activity weakens on a time scale of perhaps ten disk rotations (Sellwood & Carlberg 1984). 3 At this point the minor gas component (Section 2.11) takes on a dynamically important role; while dense clouds of gas are accelerated by the spirals in the same manner as are the stars, they are able to dissipate random motion quickly through supersonic collisions that allow the excess energy to be radiated away. The gas clouds themselves, and the stars that form within them, therefore constitute a low velocity dispersion component that is able to maintain the dynamical responsiveness of the combined star-gas disk. Sellwood & Carlberg (1984) estimated that a birth rate of a few stars per year over the entire disk of a galaxy would be sufficient to sustain spiral activity indefinitely. Subsequent work (Carlberg & Freedman 1985; Toomre 1990; Roskar et al. 2008a) on isolated disks, and fully cosmological simulations (e.g. Agertz et al. 2011), seems to confirm that no matter how the dissipation is mimicked, the disk continues to support transient spiral patterns. This behavior provides an attractive explanation for the long-noted (e.g. Oort 1962) contrast between the striking spirals manifested by galaxies having abundant gas to the featureless appearance of S0 galaxies that have very little gas.
It has been clear for over 50 years that older stars in the neighborhood of the Sun have larger velocity spreads than do younger stars (Wielen 1977; Nordström et al. 2004). It seems unsatisfying to suppose that older stars were born with larger random velocity components, since it requires us to live at a special time when random motions at birth have just become small, but this suggestion has been advocated (e.g. Kroupa 2002). Some initial random motion seems likely in the disturbed conditions of disks in the early Universe when the oldest stars formed, but the progressive increase of random motions of disk stars with increasing intermediate ages is generally attributed to scattering processes. Both massive gas clumps (Spitzer & Schwarzschild 1953) and spiral patterns (Barbanis & Woltjer 1967) are still considered viable as scattering agents.
3.2.1. Solar neighborhood data
Fig. 4 shows the variation of stellar velocity
dispersion components with estimated age, as presented by
Holmberg et
al. (2009).
(The small scatter about the trend among the points for the older stars is
somewhat odd.) These results are synthesized from the heroic
Geneva-Copenhagen survey (herafter GCS) of ~ 14 000 F- and
G-dwarf stars by
Nordström et
al. (2004),
with repeated radial velocity
measurements of all the stars to eliminate binaries, as well as
improved stellar parameter and age calibrations
(Holmberg et
al. 2007),
and the revised Hipparcos distances and proper motions
(van Leeuwen 2007).
Holmberg et
al. (2009)
use the usual notation
U,
V, and
W for the
radial, azimuthal, and vertical velocity
spreads as seen from the Sun, where others may use
R,
, and
z for the
radial, azimuthal and vertical dispersions anywhere.
Casagrande et
al. (2011)
reanalyzed the same sample adding infrared
fluxes for about half the stars to obtain new estimates of stellar
parameters and ages, and again found the total velocity dispersion
rose steadily with age (their Fig. 17), even when they excluded
metal-poor stars.
 |
 |
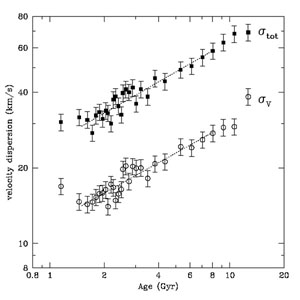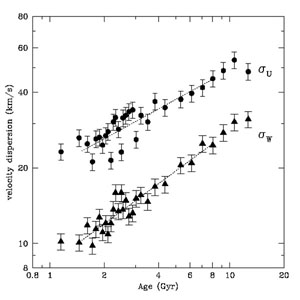
Figure 4. Estimates of the second moments of stellar velocities from the Geneva-Copenhagen survey. The symbols with error bars show the estimated spreads of the three velocity components in Galactic coordinates: in the upper panel, U is in the radial direction and W in the direction normal to the plane. The spread of V in the azimuthal direction and the total dispersion are shown in the lower panel. The stars were divided by estimates of their ages and the fitted lines ignore the two youngest and the two oldest groups. From Holmberg et al. (2009). |
Assigning ages to individual stars is highly controversial (see Soderblom 2010 for a review), and the precise trend with age has therefore been the subject of much debate. Reid et al. (2007) suggest that the ages of individual stars assigned by Nordström et al. (2004) and revised by Holmberg et al. (2007) are compromised by large random errors. Were this the case, then the real trends with age would have to be even steeper than shown in Fig. 4, since large age errors will flatten a trend, as found by Casagrande et al. (2011) when they included stars with more uncertain ages.
On the other hand, Edvardsson et al. (1993) and Quillen & Garnett (2001) claimed a more nearly constant velocity dispersion with age, except for very old stars that have a larger dispersion. Soubiran et al. (2008) also found an almost flat dispersion with age, although it is unclear whether their exclusion of probable thick disk and halo stars, based at least in part on their kinematics, is affecting the trend. If a constant dispersion with age were correct, and if the small samples of stars used in these studies were drawn from the same population as those selected by Holmberg et al. (2009), then the age errors that give rise to the steady trends seen here in Fig. 4 and in Fig. 17 of Casagrande et al. (2011) would have to correlate with the kinematics. It therefore seems more likely that claims of a flat trend result from large age errors or selection against stars with large peculiar velocities. Furthermore Aumer & Binney (2009) found that blue main-sequence stars, which must be young, have much smaller random motions than do red main-sequence stars, which can have a wide range of ages. Using color as a proxy for age assumes a well-behaved star-formation rate in the disk, which has probably declined slowly over time (e.g. Fraternali & Tomassetti 2012). Aumer & Binney (2009) constructed a model to fit the data that also favored a steady increase of velocity dispersion with time.
In fact, the in-plane components of the GCS stars do not have simple
Gaussian velocity distributions (Fig. 5), as first
deduced from the Hipparcos data by
Dehnen (1998).
Not only is the overall distribution of the V components quite
skew with an "asymmetric drift"
(
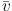< 0 as expected, BT08;
Schönrich &
Binney 2012),
but the distribution is characterized by multiple "streams" that are
distinct at a high level of significance
(Bovy et al.
2009).
The streams are both far too massive and have a spread in metallicities
to be dissolved star clusters
(Famaey et
al. 2007;
Bensby et al.
2007;
Pompéia et
al. 2011).
Hahn et al.
(2011)
examined the nearby stars of the Sloan Digital Sky Survey (SDSS
York et al.
2000)
and RAdial Velocity Experiment (RAVE
Steinmetz et
al. 2006)
finding similar, but less distinct,
substructure. Blurring of the velocity structures is to be expected
for stars in these larger surveys, which do not have
Hipparcos-quality astrometry and distances, with consequent loss
of precision in the sky-plane velocity components.
Antoja et al.
(2012)
traced
some of these features in somewhat more distant stars of the RAVE survey.
 |
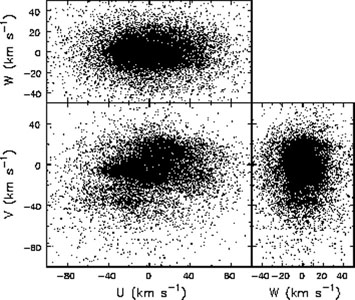Figure 5. The stellar velocities from the Geneva-Copenhagen survey (Holmberg et al. 2009), corrected for solar motion (U⊙, V⊙, W⊙) = (11.1,12.24,7.25) km s-1 (Schönrich et al. 2010). Note the substantial substructure in the (U, V)-plane that is not reflected in W. |
The substructure in Fig. 5 probably arises from the dynamical influence of density perturbations in the disk and a number of attempts have been made to model it. De Simone et al. (2004) found that multiple, imposed transient spiral perturbations were able to create qualitatively similar substructure in the stellar velocity distribution. On the other hand, individual features have been interpreted as responses to assumed models for the bar (see also Dehnen 2000, Minchev et al. 2010, see also Kalnajs 1991), or to specific spiral models (Quillen & Minchev 2005; Pompéia et al. 2011; Antoja et al. 2011), or both (Quillen 2003; Chakrabarty 2007; Antoja et al. 2009). Finally, Sellwood (2010, see also Hahn et al. 2011 and McMillan 2011, 2013) did not need to adopt a perturbing potential, but instead used action-angle variable analysis to identify the Hyades stream as resulting from scattering by a recent Lindblad resonance. It is likely that the different streams have different origins and a combination of these ideas would be needed to explain all the features.
Returning to Fig. 4, the data show that the second moments of the peculiar velocities differ in all three components – i.e., the velocity ellipsoid of nearby disk stars has a triaxial shape that apparently grows roughly homologously with age. Seabroke & Gilmore (2007) argue that the multiple streams in the U - V plane (Fig. 5) make the second moment a poor measure of the velocity spread. However, the distribution in the U-W plane is much smoother and it is worth noting that the rising trend of the V component in Fig. 4 maintains a constant fraction of the radial component at the ratio expected from epicycle theory (BT08, Eq. 8.117) in a galaxy with an approximately flat rotation curve.
In Galactic components, the dispersion in the radial direction is the largest, the azimuthal component is intermediate, while the smallest is the component normal to the disk plane, being only about half as large as the radial velocity dispersion. A flattened shape appears to be representative of that in other disk galaxies (Bottema 1993; Gerssen et al. 2000; Herrmann & Ciardullo 2009; Bershady et al. 2011), although Gerssen & Shapiro (2012) claim evidence that the axis ratio varies along the Hubble sequence.
Smith et al. (2012) present a study of local disk kinematics using the "Stripe 82" data from SDSS, although they make no attempt to assign ages to stars. Instead they divide stars by metallicity and present-day z-height below the disk plane and devise a procedure to estimate separate dispersions of the thin- and thick-disk stars that, however, must become increasingly difficult for metal-poor stars and those at large distances from the midplane. While their results for thin-disk stars with -0.5 < [Fe/H] < 0.2 are consistent with those from other studies, they found the velocity ellipsoid is distinctly rounder for more metal-poor stars that also have higher velocity dispersions.
Lewis & Freeman (1989) found that the velocity dispersion in the Milky Way disk has a steep outward gradient over a wide radial range, as the above-cited studies also found in other galaxies. A gradient is, of course, expected on local stability grounds (Eq. 18), but the radial gradient must somehow combine with the velocity ellipsoid shape and disk surface density to create a vertical thickness scale that appears to be independent of radius for many galaxies (van der Kruit & Searle 1981; Kregel et al. 2002). This conspiracy of disk properties has yet to be fully explained.
Lynden-Bell & Kalnajs (1972) showed that, away from resonances (Section 2.8), a spiral perturbation that grows and decays adiabatically (on a time scale long compared with orbital and epicycle periods) leaves the stellar motions unchanged. Stars do work on, or receive energy from, a potential perturbation as it grows, but these changes are undone as the wave decays, leaving only oscillatory ripples in the phase-space density that average to no change (5Carlberg & Sellwood 198), except at resonances.
Wave-particle interactions at resonances do, however, cause lasting changes to the orbits of stars, and Lynden-Bell & Kalnajs (1972) showed that stars at the ILR lose angular momentum on average, while those at the OLR gain. Changes at corotation could be of either sign, depending on the sign of the gradient of the angular momentum density of stars around the resonance (see Section 2.6).
The changes given by Eq. (20) become
-functions at
resonances in the limit
ℑ(
) =
→
0, which
Lynden-Bell &
Kalnajs (1972)
take.
4
However, changes are smooth when broadened by time dependence, and
Carlberg &
Sellwood (1985)
compute the lasting changes under the assumptions that the wave both
grows and then decays exponentially.
In a rotating, but otherwise steady, nonaxisymmetric potential test particles conserve neither their energy, nor their angular momentum, but Jacobi's integral,
 |
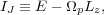(25) |
is conserved. Thus changes in energy and angular momentum are related
as 
E =
p
Lz. This is illustrated in
Fig. 6, which is drawn for the midplane of an
axisymmetric potential (see also
Lynden-Bell &
Kalnajs (1972)
their Fig. 2). Circular orbits have the minimum energy
Ec for a given Lz, which
marks the boundary of the shaded region, while orbits with E >
Ec are
eccentric. Equation (25) constrains particles that are
scattered by a nonaxisymmetric perturbation to move along lines of
fixed slope
p as
illustrated by the arrows, which are marked at the principal resonances
because those are the only places where lasting changes occur.
 |
Figure 6. The Lindblad diagram for a
razor-thin disk galaxy model.
Circular orbits lie along the full-drawn curve and eccentric orbits
fill the region above it. Angular momentum and energy exchanges
between a steadily rotating disturbance and particles move them
along lines of slope
|
There is an important difference between scattering at Lindblad
resonances and at corotation. A star near corotation may suffer quite
a large change in its angular momentum, but because
dEc / dLz =
p at this
radius (Fig. 6),
it neither gains nor loses random energy (to first order); all the
energy change is invested in changing the radius of the guiding center
(Eq. 6). This is a characteristic feature of radial
migration (Section 3.3). The situation is different
away from corotation, where there is an excess of energy available to
increase random motion, provided that stars inside corotation lose
Lz while those outside gain.
Sellwood & Binney (2002) (their Eq. 6) showed that the first order change in radial action of a star caused by a single spiral wave is related to its change in angular momentum via
 |
(26) |
Since l = 0 at corotation, any
Lz
causes no change to JR,
as noted. Furthermore,
Lz
< 0 at the ILR where l = -1 and
Lz
> 0 at the OLR where l = +1. Thus outward transfer of
angular momentum from the inner to the outer Lindblad resonance causes
JR > 0, or heating, at both, as is also
clear from Fig. 6. A succession of transient
spiral modes with a
variety of pattern speeds will cause the in-plane components of
stellar random motion to increase generally over the disk.
Note that the changes caused by transient spiral modes increase only
the in-plane random motions, not the component normal to the plane as
predicted by
Carlberg (1987)
and confirmed by
Sellwood (2013b).
The reason (Section 2.8) is that
coupling between the spiral
perturbation and vertical motion is expected to be very weak because
the frequency 
of small
vertical oscillations of a star near the
midplane (Eq. 8) is generally high compared with the
Doppler shifted frequency
m| -
p| at
which it encounters the perturbation, making its vertical motion
adiabatically invariant. While a majority of stars rise out of the
harmonic region, the fraction that have a low enough vertical frequency
to experience a vertical resonance with a spiral perturbation is
believed to be quite small.
The discussion in the previous paragraph assumed Newtonian gravitational forces, and softening in simulations (Section 2.12) can change the behavior. Increasing the gravitational softening length weakens the restoring forces to the midplane, decreasing the vertical frequency and possibly allowing vertical resonances to become dynamically important (see Solway et al. 2012, their Fig. 9). On the other hand, simulations with small softening, but modest numbers of particles, may thicken due to relaxation (Sellwood 2013b). Thus the modeling of disk thickening in simulations is somewhat delicate.
Coherent bending waves are another possible mechanism to increase the
vertical velocity dispersion. The mechanics of bending waves is
complicated (see
Sellwood 2013a
for a recent review). However, we do
know that a bending wave may travel across a stable disk
(Toomre 1983;
Weinberg 1991)
until it is damped as it approaches a vertical resonance
(Sellwood et
al. 1998),
with the wave energy going into localized vertical heating. It is also known
(Toomre 1966;
Araki 1985)
that a disk in which the velocity ellipsoid is flattened such that
R
3 z will
buckle and
thicken until the axis ratio is approximately this value
(Sellwood 1996;
Rodionov &
Sotnikova 2013).
5
However, the velocity ellipsoid of local stars in the Milky Way is not
flattened enough to be near this stability boundary.
Another possible heating mechanism is infall of cosmic substructure (e.g. Kazantzidis et al. 2009). While infall of massive clumps in their simulations, and those of others, is quite disruptive and can probably be excluded (Section 4.2), a gentler bombardment by smaller clumps may cause more gradual heating. However, a prediction of Kazantzidis et al. 2009 is that satellite bombardment should create velocity dispersions that are roughly constant with radius, whereas data on the Milky Way (e.g. Lewis & Freeman 1989) indicate a strong decline with radius to distances well beyond the solar circle. Thus, while some heating by infall cannot be excluded, it is clearly not the dominant process.
Since the data (Fig. 4) show that the out-of-plane motions rise with about the same slope as the in-plane part, it seems unlikely that spiral waves, neutral bending waves, or buckling instabilities are important in setting the shape of the local velocity ellipsoid in the local Milky Way. It therefore seems that scattering by collective waves cannot be the whole story.
3.2.4. Scattering by dense mass clumps
Spitzer & Schwarzschild (1953) argued that massive clumps of gas were needed to account for the increase of peculiar stellar velocities with their ages, and therefore hypothesized the existence of giant molecular cloud complexes (GMCs) long before their existence was established. Their original calculation of scattering by dense mass clumps was extended to 3D by Lacey (1984). In his analysis, as in the earlier work by Spitzer & Schwarzschild (1953), the star-clump interaction was computed in the impulse approximation, in which scattering is assumed to occur over a distance that is short compared with both the size of the star's epicycle and the scale on which the galactic gravitational potential changes.
Lacey (1984)
found that co-orbiting mass clumps are quite efficient
at redirecting peculiar motions out of the plane, but rather
inefficient at increasing them. He also concluded that cloud
scattering should cause the vertical dispersion
W to be
intermediate between the radial
U and azimuthal
V
components. This result seemed physically plausible on energy
equipartition grounds: scattering by massive clouds redirects the
peculiar motions of stars through random angles, and therefore
isotropizes the motions as far as the epicycle gyrations allow.
However, this again is inconsistent with the data
(Fig. 4), where
W is the
smallest component. In order to account for the observed flattened shape,
Carlberg (1987)
and
Jenkins & Binney
(1990)
developed the plausible argument that the in-plane
dispersion is driven-up more rapidly by spiral heating than scattering
is able to redirect those motions into the vertical direction. Their
argument seemed to offer strong support for the transient spiral mode
picture
(Sellwood 2000),
but it now appears to be incorrect.
Ida et al. (1993) found that cloud scattering alone would lead to the vertical component being the smallest, with the precise axis ratio of the velocity ellipsoid depending on the local slope of the rotation curve. Simulations by Shiidsuke & Ida (1999), and others (see e.g. Villumsen 1985; Hänninen & Flynn 2002), confirmed their expectation.
The reason for the discrepancy with Lacey's prediction was clarified
by
Sellwood (2008b),
who presented local simulations of scattering of
test particles by massive co-orbiting particles. He artificially
restricted the range of the gravitational forces from the heavy
particles, which vanished at distances greater than some
dmax. Figure 7 shows the
equilibrium ratio of the vertical to radial velocity dispersions
W /
U plotted
as a function of the adopted dmax. The ratio settles to
something close to the energy equipartition prediction when none but
the closest heavy scatterers perturb the stars but, as the range of
scattering was increased in separate experiments, the equilibrium
ellipsoid gradually flattened and approached the shape predicted by
Ida et al.
(1993)
for no cut off.
 |
Figure 7. The equilibrium axis ratio of the velocity ellipsoid of particles plotted as a function of the limiting range of the perturbation forces from the heavy particles. See Sellwood (2008b) for a description of the calculations. |
The flattened shape of the ellipsoid is determined by the fact that the perturbing clouds are located within the disk, leading to an aspherical distribution of impact parameters, with the consequence that deflections from the more distant clouds preferentially redirect the in-plane velocity components. Lacey (1984) and Binney & Lacey (1988) neglected distant encounters, and therefore missed this effect. However, the familiar argument that every decade in distance makes an equal contribution to scattering also ceases to hold in disks (Section 2.2), and the contribution to scattering by clouds that are more distant than several disk scale heights drops away rapidly. Thus it is the clouds at in-plane distances of just a few disk thicknesses that do most of the redirecting.
Smith et al. (12012) confirmed the predicted velocity ellipsoid shape for the metal rich stars in their data, but reported a rounder ellipsoid for the hotter, and probably older, metal-poor stars. Further work is needed to confirm this metallicity dependence, which may have been biased by the difficulty of separating thin- from thick-disk stars. Note that Holmberg et al. (2009) (see Fig. 4) found an ellipsoid shape that was almost constant with age, and at most only mildly rounder for the older stars.
The preceding calculations of scattering by mass clumps ignored all collective effects. Not only are disk galaxies subject to spiral perturbations, which themselves scatter stars, but the co-orbiting GMCs induce a collective response from the surrounding stellar disk (Julian & Toomre 1966) that substantially enhances their effective mass, a complication that is ignored in most studies of cloud scattering. An exception was provided by Toomre & Kalnajs (1991), who studied scattering by both a density perturbation and the supporting response from the surrounding matter. The density fluctuations in their local simulations arose from the shot noise of the particles, while the same particles also took part in the supporting response. By applying a radial damping term, they may have unwittingly prevented the growth of instabilities (Sellwood 2012), making their work a particularly clean calculation of the heating rate due only to the polarized disk response to co-orbiting mass clumps.
Since molecular gas is mostly (Nieten et al. 2006; Koda 2009; Gratier et al. 2010; Efremov 2010), but not entirely (e.g. Corder et al. 2008; Schinnerer et al. 2013), concentrated in spiral arms it is probably futile to draw a sharp distinction between spiral arms and the wakes of dense gas clumps, and a correct treatment would be to calculate the effects of spiral formation and gas dynamics in the combined star and gas disk. Binney & Lacey (1988) took a step in this direction, but a full calculation may remain unreachable for some time if one tries to include a self-consistent treatment of the formation and dispersal of the gas clumps: molecular gas concentrations probably grow in the converging gas flow into a spiral arm, and are subsequently partly dispersed by star formation. D'Onghia et al. (2013) also showed that massive clumps provoke spiral responses, but the spiral activity probably included some self-excited collective modes, since it persisted after the perturbers were removed.
Thus the studies of scattering in disks reviewed earlier make the simplifying assumption that spirals and mass clumps are distinct agents. This assumption at least separates the problem into tractable pieces. Perhaps it can be justified if the wakes of cloud complexes can be lumped with spirals into a single scattering agent that is distinct from the clouds that caused them.
3.2.6. Conclusions on scattering
We now understand that the velocity ellipsoid in the solar neighborhood is flattened as expected from scattering by GMCs (Ida et al. 1993). While the clouds efficiently redirect peculiar velocities to maintain the observed shape of the velocity ellipsoid, they are not thought to be responsible for much heating.
The magnitude of the peculiar velocities of the intermediate age stars exceeds what cloud scattering could achieve (Lacey 1991). The old explanation for this, which may not be valid because it neglects the cumulative effect of intermediate distance encounters, was that the efficiency of scattering by clouds decreases as stars spend more time outside the cloud layer that is largely confined to the midplane. Simulations by Hänninen & Flynn (2002), that did include distant encounters, confirmed that GMCs alone are unable to account for the random motions of the oldest stars.
Thus some other agent, generally assumed to be the spirals, is needed to boost the rms velocities of intermediate age disk stars to their observed values. Even though spirals do not heat the vertical motions, they drive up in-plane random motions that are efficiently redirected by GMCs, and the velocity ellipsoid maintains an approximately constant shape as its size increases, accounting for the observed trends in Fig. 4. This picture does not exclude the possibility that the high peculiar motions of the very oldest disk stars, also known as the thick disk, have a different dynamical origin (Section 4).
Note that the behavior in N-body simulations needs to be interpreted with caution. Section 3.2.6 accounted for the observed peculiar velocities in the solar neighborhood using the combined action of two distinct mechanisms: heating by spirals with the random motions being redirected by molecular clouds. Simulations support spiral patterns that may resemble those in galaxies and, if collisionless, should not thicken because they generally omit heavy particles to represent GMCs. 6 Yet a few authors (e.g. Quinn et al. 1993; McMillan & Dehnen 2007) have worried that disks thicken in isolated N-body simulations that are heated by spiral activity.
House et al. (2011) compared the vertical heating in a simulation with the solar neighborhood data. Their simulation, which was probably heated in part by spirals, included the cosmologically expected infall of pieces of substructure that could increase the vertical dispersion, and also modeled the full "gastrophysics" of cooling, star formation and feedback. However, they employed gas (and star) particles having the masses of GMCs, which therefore lacked the spatial and mass resolution to form dense clumps that are crucial to shaping the velocity ellipsoid.
Collisional relaxation, which is much more rapid in disks (Sellwood 2013b and Section 2.2), is a more likely explanation for redirecting in-plane motions to thicken disks in simulations. 7 Thus, the simulated vertical heating rate, in particular, will depend on the number of particles employed, and comparison with the observed vertical heating of disk stars in the Milky Way (e.g. House et al. 2011) is premature without careful numerical convergence tests.
3.3. Radial migration and mixing
For years, the focus of spiral scattering was on heating at Lindblad resonances, and changes at corotation went unreported. Sellwood & Binney (2002) were therefore surprised to find that a transient spiral mode causes greater angular momentum changes to stars at corotation than occur at the Lindblad resonances, as shown in Fig. 8. These more substantial changes had not attracted attention because they do not heat the disk (Eq. 26), and stars largely change places in a dynamically neutral manner. However, they do have important consequences for the distribution of chemical abundances among the disk stars (Roskar et al. 2008b; Schönrich & Binney 2009a; Minchev et al. 2013).
 |
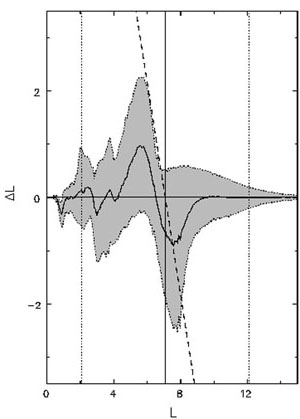Figure 8. Changes in angular momentum, L, resulting from a single transient spiral mode. The shaded region includes 90% of the particles and the solid curve shows the mean change. The vertical solid line marks the location of corotation, while the dotted lines mark the Lindblad resonances. The dashed line has slope -2. From Sellwood & Binney (2002). |
Changes to the guiding center radii caused by a series of transient spiral modes with corotation radii scattered over a wide swath of the disk will cause stars to execute a random walk in radius with a step size ranging up to ~ 2 kpc. The resulting strong radial migration, called churning, has implications for abundance gradients and age-metallicity relations. The apparent metallicity gradient is also blurred by epicyclic motions, which can readily be subtracted for an individual star without having to integrate the orbit (e.g. Yu et al. 2012), since the guiding center radius of a star is determined only by its angular momentum (Eq. 6).
The topic of radial migration is bedeviled by the fact that many authors have conflated the process first described by Sellwood & Binney (2002) with the general redistribution of angular momentum that occurs with any nonaxisymmetric disturbance. The fact that spirals, bar formation, the excitation of responses by satellites, etc., redistribute angular momentum across the disk of a galaxy had been understood for decades. However, the recently discovered changes at corotation of a transient spiral mode have the two unique properties of neither heating the disk nor causing it to spread, as described next. All other forms of angular momentum transport do both these things. Even processes that are not associated with lasting angular momentum changes, such as increasing epicycle motions or of trapped particles that cross and recross a resonance, have been described as "radial mixing." While this phrase may be too deeply embedded to be redefined, "radial migration" and "churning" are less widely used and I suggest these terms be reserved to describe only the changes at corotation of a transient spiral mode.
While these other processes may play a role in redistributing matter radially, the low velocity dispersion of disks limits the extent to which heating at Lindblad resonances can have occurred, as discussed in 3.2.2. Churning by spiral waves over the lifetime of the disk could, in principle, cause far more mixing with very limited heating, as found by Sellwood & Binney (2002) and Solway et al. (2012) (see Fig. 9).
3.3.1. Mechanism of radial migration
Stars near corotation move slowly with respect to the spiral perturbation and therefore experience almost steady forcing from the wave, which allows large changes to build up – a process that is analogous both to surfing on ocean waves and to Landau damping in plasmas, although the consequences differ. Stars orbiting just behind the density excess are attracted forward by it and therefore gain angular momentum. However, the result of gaining angular momentum is that the star moves onto an orbit of greater guiding center radius (Eq. 6), and its angular frequency about the center therefore decreases. If the star were just inside corotation and therefore gaining on the density excess, the change can cause it to rise to a radius just outside corotation where it begins to fall behind. This behavior is described as a horseshoe orbit. Conversely, stars just ahead of the perturbation are pulled back, lose angular momentum and sink inwards, where they orbit at higher frequency. Those outside corotation, where the perturbation gains on them, could lose enough angular momentum to cross corotation and begin to run ahead of the wave. As long as the gradient ∂ f / ∂ Lz is fairly shallow, roughly equal numbers of stars gain as lose, and they largely change places. The process affects stars with small peculiar velocities most strongly, since larger epicyclic motion leads to less coherent forcing by the spiral potential.
Were the spiral potential to maintain a fixed amplitude, stars on horseshoe orbits would be described as trapped. As they are moving slowly with respect to the wave, it would take them a long time to reach the next density maximum where the changes just described would be exactly undone. However, if the amplitude of a transient spiral mode has decreased by the time the star reaches the next density peak, it may no longer be trapped and will continue to move with a lasting change to its angular momentum.
Adopting variables suited to motion near corotation of a steady potential perturbation, Sellwood & Binney (2002) found that the radial extent of the region where these horseshoe changes occur varies as the square root of the perturbation amplitude, and therefore widens as a perturbation grows. At the same time, the more distant "trapped" stars move more rapidly in the frame of the perturbation, and the shortest period of a trapped star decreases as the inverse square root of the potential amplitude. They found the spiral was strong for less than half the horseshoe period for most trapped stars, which therefore undergo a single change.
Horseshoe orbits are also responsible for limiting the amplitude of the spiral. For a disturbance to grow, the response of the stars to the growing potential must reinforce the perturbed density, at least until it saturates. Sellwood & Binney (2002) also argued that the maximum amplitude of a spiral is limited by the widening horseshoe region where stars are driven away from, instead of toward, the density maximum. This change kicks in suddenly because growth is linear in the disturbance potential, but the horseshoe region grows as its square root.
3.3.2. Other radial mixing processes
Any process that redistributes angular momentum mixes stars and gas that originated at different radii, and even the transient spiral modes that churn the disk also transport angular momentum to a much lesser degree. However, in contrast to the changes brought about by churning, redistribution of angular momentum across the disk always increases random motion and alters the large-scale surface density profile of the disk.
The role of bars as agents that mix the stars and gas of a disk has long been recognized (e.g. Hohl 1971; Friedli et al. 1994), and has received intense recent attention. The possible effect of resonance overlap between the bar pattern and the outer spiral was raised by Quillen (2003), see also Minchev & Quillen (2006), and developed by Minchev & Famaey (2010) for test particles in assumed nonaxisymmetric potentials of plausible bars and spirals. Since they adopted perturbations that grew to steady amplitudes, they clearly were not exploring the process described by Sellwood & Binney (2002). Instead they found, as had Little & Carlberg (1991, although without comment), that single perturbations created regions in which particles were simply trapped to cross and recross corotation with minimal angular momentum changes at the Lindblad resonances. However, simulations with two imposed disturbances revealed chaotic behavior when resonances of the two patterns overlapped, which Minchev & Famaey (2010) described as "nonlinear" interaction. The substantially greater changes in the angular momenta of the particles were also associated with disk heating (Minchev & Quillen (2006)). These studies raise the possibility that additional angular momentum transport could even occur were galaxies able to support multiple long-lived nonaxisymmetric structures. Quillen et al. (2009) also used the test-particle technique to show that the orbits of disk particles are "mixed" when perturbed by an orbiting satellite.
Results from N-body simulations are of greater interest, since the perturbations that cause the angular momentum changes are generated self-consistently and have physically reasonable time dependence. Brunetti et al. (2011) calculated diffusion coefficients in disks that form bars and spiral patterns finding, as seems reasonable, that angular momentum changes are lower in disks with higher Q (Eq. 18). Minchev et al. (2011, 2012a) report simulations that formed bars and spirals, in which they claim evidence of enhanced angular momentum changes due to resonance overlap. They also highlight disk spreading, which is largely due to the angular momentum changes during bar formation (see Section 5.2), and also prolonged changes at the corotation resonance of a bar, which are likely caused by particles that are trapped to cross and re-cross the resonance and therefore cannot sensibly be described as something as irreversible as mixing.
3.3.3. Radial migration in simulations
Roskar et al. (2008a) computed an isolated gas plus stars galaxy model that tracked star formation and metallicity evolution. The churning of the disk by a succession of transient spiral modes caused extensive migration. Some heating was caused by the smaller changes at the Lindblad resonances of spirals in their models, which is unavoidable, and they reported a change in the gradient of mean stellar age near the outer edge of the disk, which must have been created by the outward migration of particles. Roskar et al. (2008b) went on to demonstrate that migration led naturally to an age-metallicity relation similar to that in the Milky Way. A later work (Loebman et al. 2011) studied the formation of a thickened disk comprised of outward migrating stars with enhanced [α/Fe] ratios and lower mean orbital speed. Bird et al. (2012) found that mixing is more extensive when spiral activity is invigorated by star formation, although the level of spiral activity in their models depended strongly on the "gastrophysical" prescription adopted. They showed that migration persists even for particles with large oscillations about the midplane, and they determined migration probabilities from their simulations.
Figure 9 (from Solway et al. 2012) shows that the home radii of stars can migrate either inwards or outwards by many kpc, while the formation of a bar causes some comparatively mild additional mixing. Radial migration in the thick disk is only slightly weaker than in the thin disk, because the spiral potential that drives migration decays only slowly away from the plane. In fact, the slightly smaller average changes of the thick-disk particles were probably caused more by their larger in-plane random velocities than by their greater vertical oscillation (Solway et al. 2012, their Fig. 10). This is the likely reason that Bird et al. (2013) found that radial migration was less effective in the hotter, and generally older, particles of the inner disk of their model.
 |
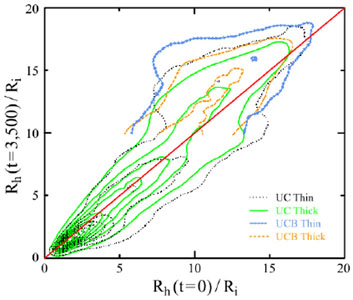Figure 9. Comparison of initial home radii with home radii after ~ 10 Gyr of evolution for particles in two simulations by Solway et al. (2012). For Milky Way scaling, the radial unit is 0.75 kpc. Simulation UC did not form a bar, whereas a bar did form in simulation UCB, and contours are drawn separately in different colors and line styles for the initially thin- and thick-disk populations. The barred region is omitted because Rg (Eq. 6) cannot be defined in a strongly nonaxisymmetric potential. |
Roskar et al. (2012) presented a detailed study of radial migration in their simulations. They identified the locations, relative to the spiral density maxima, of particles that gained or lost large amounts of angular momentum and confirmed that even particles that moved rapidly over a large radial distance remained on near-circular orbits.
One of the advantages of using action-angle variables to describe the motions of stars (Section 2.4) is that the actions are adiabatic invariants. Broadly, this means that they are conserved quantities when the orbit of the star is subject to slow changes, except where resonances arise (see BT08, Section 3.6 for a more careful statement). For example, Lynden-Bell (1963) used the invariance of radial action of a star to argue that orbital eccentricity would be invariant during gradual changes to the potential with no change to the angular momentum of the star. However, transient spirals change the angular momentum of stars at corotation without changing the radial action, and therefore eccentricity is not invariant during these changes.
Nevertherless, the radial action, JR, is a useful
adiabatic invariant during disk evolution except, of course, from the
nonadiabatic changes at Lindblad resonances, where l=±1 in
Eq. (26). For nearly circular orbits JR →
a2 /
2, with a being the radial excursion of the star
(Lynden-Bell &
Kalnajs 1972).
For a well-mixed set of stars of fixed JR, we have
< a2 > =
2< vR2 > /
2 in the
epicycle approximation, and therefore JR
≈ < vR2
> / . Thus, during
radial migration
< vR2
> ∝ for this
group of stars, i.e. their radial
dispersion decreases during outward migration, as found by
Minchev et al.
(2012b),
and vice versa.
Solway et al. (2012) also showed that vertical action Jz, and not vertical energy, is the conserved quantity when stars migrate. Their conclusion stood out far more clearly when vertical action was calculated exactly (Eq. 9), than when the simple epicycle approximation was used (e.g. Minchev et al. 2012b). A somewhat puzzling finding by Solway et al. (2012) was that Jz was conserved on average, but not precisely for individual particles; which may have been due to gradual relaxation that afflicts all N-body simulations of disks (Sellwood 2013b).
Since its vertical action is adiabatically invariant during migration, the vertical oscillation amplitude of a star varies with the strength of the vertical restoring force, which in turn changes with disk surface density. A group of particles that have migrated outward in a nongrowing disk of declining surface density must have an increased scale height and a decreased velocity dispersion (Schönrich & Binney 2012; Roskar et al. 2013). The vertical thickness would be squeezed by the increasing mass density that occurrs in a growing disk, but younger stars formed in the outer disk must still reside in a distinctly thinner layer than that of the outward migrating stars.
3.3.5. Tests for radial migration in the Milky Way
Currently, there has been no decisive test to confirm that radial migration really does occur in the Milky Way disk or elsewhere. But there are a number of strands of indirect evidence to suggest that the mechanism does occur.
Haywood (2008) found evidence for radial migration in a study of the metallicity distribution of solar neighborhood stars that suggested some stars were formed elsewhere in the disk. Lee et al. (2011) claim evidence for radial migration in the thin disk on the grounds that metallicity is uncorrelated with orbital eccentricity, but found a decreasing orbital velocity with metallicity in the thicker disk. Yu et al. (2012) reported a decreasing metallicity gradient with age of Milky Way thin-disk stars, which is the expected consequence of radial migration.
Bovy et al. (2012b) corrected data from SDSS for the selection function of the survey to determine the properties of the underlying stellar population. They found a continuous distribution of abundance-dependent disk structure with increasing scale height and decreasing scale length which they argued strongly favors "inside-out" disk formation combined with gradual internal evolution through mechanisms such as radial migration. Both Bensby et al. (2011) and Cheng et al. (2012), in separate studies of quite different stellar populations, also found a short scale length for thick-disk stars, which are less well mixed because these populations are dynamically hot.
Haywood (2012) concluded that the metallicity distribution of disk stars seemed consistent with some degree of migration, but drew attention to a number of puzzling features. He cited very tentative evidence of a steplike feature in the radial distribution of metallicities (Hill et al. 2012) that, if confirmed, suggests that migration in the Milky Way may not have been efficient. However, Yong et al. (2012), in a study of open star clusters in the disk of the Milky Way, did not find a discontinuity in the abundance gradient at the solar radius, but instead found evidence for a change to a shallower slope at around 12 kpc.
Much stronger tests will emerge from current and future surveys. The Gaia mission (Perryman et al. 2001) will yield the kinematics of stars over a large fraction of the Galaxy in overwhelming detail. More detailed kinematics and chemical abundance measurements are being, or will soon be, collected in surveys such as APOGEE (Allende Prieto et al. 2008], LAMOST (Deng et al. 2012) and ARGOS (Freeman et al. 2013) – see also Rix & Bovy (2013). Indeed, one of the principal goals of the HERMES survey (Bland-Hawthorn et al. 2010) is to unravel the history of radial migration in the Milky Way.
3.4. Smoothing rotation curves
The rotation curve, or circular speed as a function of radius, is remarkably smooth for most galaxies (see Sofue & Rubin 2001 for a somewhat dated review). There is no feature even where the central attraction shifts from being baryon-dominated to dark matter-dominated, which Bahcall & Casertano (1985) described as a "disk-halo conspiracy." A few authors (e.g. Kalnajs 1983; Kent 1986; Palunas & Williams 2000) have drawn attention to "bumps and wiggles" in long-slit rotation curves, some of which correspond to photometric features in the light profile. While this is undeniable evidence for significant mass in the disk, the underlying cause of these small-scale features may be spiral arm streaming rather than substantial fluctuations in the radial mass profile of the disk.
Spiral instabilities may also be responsible for featureless rotation curves, as first argued by Lovelace & Hohlfeld (1978). While running simulations with a different purpose, Sellwood & Moore (1999) noted that as the disk grew in their models with a dense central mass and a (rigid) cored outer halo, the mass distribution in the disk rearranged itself such that the resulting rotation curve was remarkably featureless. They noted that they obtained this result with a number of differing rules for the angular momenta of particles added to the disk.
A more controlled example is illustrated in Fig. 10 (Sellwood, in preparation). In this simulation, the initial model was the Mestel disk that has a circular speed independent of radius shown by the dotted line in the right panel and, in this case, only one-third of the central attraction is from the disk with remaining two-thirds due to a rigid halo. The dashed lines show the consequences to the surface mass profile and rotation curve of adding, over a period of less than one disk rotation, an extra ring of matter composed of live particles to this archetypal featureless model. The model quickly developed strong spiral patterns and after just five rotation periods, the rotation curve and the surface density distribution became featureless again, as shown by the solid lines.
 |
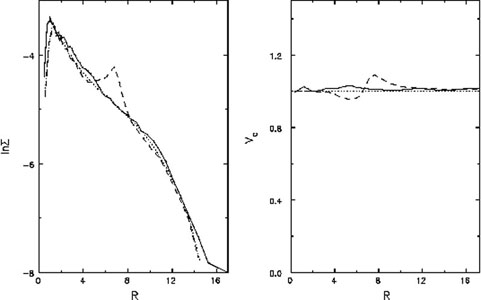Figure 10. The evolution of the surface density (left panel) and the total rotation curve (right panel) in the simulation described in Section 3.4. The dotted lines show the initial unperturbed Mestel disk, the dashed lines are drawn after a ring of material is added to the disk centered on R = 7, and the solid lines show the distribution five rotation periods later. |
The spirals that developed in this model were the result of two unstable modes that were provoked by the density ridge. Local stability analysis of a disk with a ridgelike density feature (Sellwood & Kahn 1991) predicts that, for each sectoral harmonic, the normal modes are wave pairs with corotation on opposite sides of the ridge. However, only those wavelike distortions to the ridge that can excite a strong supporting response from the surrounding disk are unstable. The angular periodicity that excites the strongest supporting response depends on the X parameter of swing-amplification theory (Eq. 19), and the most rapidly growing pair of modes is for m = 3 for the disk mass in this simulation. As the amplitudes of the modes rise, horseshoe orbits (Section 3.3.1) develop at both corotation resonances but, unlike in a featureless disk, the presence of the ridge causes the resulting Lz changes to be strongly out of balance at corotation for both modes. Thus far more particles are removed from the ridge than are added to it, causing the density profile of the disk to flatten, as shown by the solid curves in Fig. 10.
Thus it seems that the distribution of angular momentum in the baryonic material that makes galaxy disks does not need to be able to account for the featureless character of most galaxy rotation curves, and small-scale variations in any reasonable distribution will be erased by spiral activity. The experiments of Sellwood & Moore (1999), together with results from more realistic modern simulations (Abadi et al. 2003, Agertz et al. 2011) hint that this effect may be substantial enough to control the overall shape of the rotation curve, although further work is needed to establish this more interesting conclusion.
3.5. Angular momentum redistribution
For a star in a rotationally-supported disk, the angular momentum
Lz ~ RVc is much greater than the
typical radial action JR ~
aR,
with a being the radial
excursion. Thus, JR ≪ Lz,
and Eq. (26) therefore requires that
Lz
≪
Lz at Lindblad resonances. The implication is that
spirals do not cause large changes to the distribution of angular
momentum among the stars of a disk, as was borne out in N-body
simulations
(Sellwood & James
1979;
Bird et al.
2013).
The largest changes to the distribution
of Lz in a disk occur during bar formation
(Section 5.2), which has long been known
(Hohl 1971)
to create a high level of random motion although, even after this event,
JR ≪ Lz in the outer disk.
This conclusion is not inconsistent with the large changes in Lz at corotation, that cause stars to diffuse through the disk with little heating (Section 3.3). Changes at corotation cause stars largely to exchange places, with only a very minor net change (if any) to the large-scale distribution of angular momentum within the disk. Even the smoothing of features in the rotation curve (Section 3.4) causes only a localized smoothing of the angular momentum distribution.
Note that in growing galaxy disks, the specific angular momentum of infalling gas is expected to rise over time – the so-called "inside-out" growth of disks (e.g. Matteucci & Francois 1989; Samland & Gerhard 2003; Bird et al. 2013). The distribution of angular momentum among the stars formed from this material is expected to differ from that of the old disk. In this case, the total distribution of angular momentum within the disk changes for a quite different reason.
Thus the dynamically cool disks of stars in galaxies testify that their large-scale distribution of angular momentum cannot have been greatly altered from that at the time the stars formed. This constraint from random motion does not apply to redistribution within the gas component, however, since random motion in the gas is quickly dissipated.
3 Fujii et al. (2011) suggested the time-scale could be longer, but the spirals in their simulations are quite faint at late times. Furthermore, the dominant halo they use results in multiarm spirals that heat the disk more slowly than would patterns of lower m (Section 3.2.2). Back.
4 Note the important aspect of trapping at resonances by a steady or slowly growing disturbance is not captured by Eq. (20). Back.
5 This behavior is also affected by gravity softening. Back.
6 D'Onghia et al. (2013) included heavy particles, but did not discuss their effect on the velocity ellipsoid shape. Back.
7 McMillan & Dehnen (2007) found that thickening was suppressed when the azimuth of every disk particle was randomized after every step, in order to suppress the growth of nonaxisymmetric disturbances. However, such a procedure must also largely inhibit two-body scattering, as well as all coherent responses from the surrounding disk. Back.