Chandrasekhar (1943) pointed out that a massive object moving through a background sea of light particles would experience a drag force, known as dynamical friction. It is believed to affect globular clusters, satellite galaxies, and bars as they move or rotate inside dark matter halos. Orbital decay of satellites, or the slow-down of bars, together with the gain of energy by the halo, are important aspects of secular evolution.
Each particle in the background sea experiences an attractive gravitational impulse as it is passed by the advancing massive body. Since the attracted particles converge behind the perturber as it moves forward, the perturber in effect "focuses" the background particles into a trailing density excess, or wake. The gravitational attraction between the wake and the perturber gives rise to an apparent "frictional" drag that slows the motion of the perturber. The kinetic energy lost by the perturber is added to the random motion of the background particles.
The deceleration of a mass M, moving at speed
vM, through a
background sea of particles of uniform density
with an
isotropic velocity spread
may be written (BT08,
Section 8.1)
 |
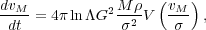(29) |
where ln
is the
Coulomb logarithm introduced in
Section 2.2. The function
V(x) describes how the retarding
acceleration varies with the speed of the perturber relative to the
random motions of the stars, and is illustrated for Maxwellian
velocity distribution in Fig. 12. A rapidly moving
perturber gives weak impulses to the background particles that create
a mild wake far downstream behind the perturber, and the drag
therefore dies away as VM → ∞. The drag on a
perturber moving slowly with respect to the rms motions of the
particles is also mild, because there is only a small excess of
particles dragging it backward over those urging it forward, and the
acceleration must also vanish as VM → 0. For a
Maxwellian velocity distribution, the drag force peaks when the
perturber moves somewhat faster than the 1D dispersion
,
i.e. the rms velocity in any coordinate direction.
 |
Figure 12. The dimensionless acceleration function V defined in Eq. (29) for the case of a Maxwellian distribution of velocities among the background particles. The function is negative because the acceleration is directed oppositely to the velocity. |
There are a number of conceptual problems with Chandrasekhar's
analysis. Foremost is that fact that the hypothesized infinite sea of
uniform density cannot be realized; away from the center of any finite
distribution of matter, the motion of the perturber would not be a
straight line but a curved orbit within the host mass distribution.
Second, each particle in the sea is supposed to have a single
interaction with the perturber, but particles must be bound to any
finite system (otherwise it would disperse), and therefore repeatedly
interact with a bound perturber. Choosing values for the density
and
velocity dispersion
appropriate for use in
Eq. (29) also presents difficulties, especially when the
mass distribution is highly inhomogeneous
(Arena & Bertin
2007).
These problems were all overcome in a seminal paper by Tremaine & Weinberg (1984b), who reformulated the analysis in action-angle variables. They found that the rate at which angular momentum is lost from a disturbing mass orbiting in a spherical system of background particles, hereafter a "halo," is given by an expression identical in form to that derived by Lynden-Bell & Kalnajs (1972) for a disk (Eq. 20 in Section 2.10) except that the DF in the spherical case expresses the density in the 6D phase space. The number of possible resonances is substantially increased, since they arise wherever combinations of the three separate frequencies (orbital, radial and vertical) for the unperturbed motion of background particles match the angular frequency of the perturbation. In a follow-up paper, Weinberg (1985) evaluated the frictional drag expected from a halo, modeled as a singular isothermal sphere, on a rotating bar, modeled a homogeneous prolate spheroid rotating about an axis in its equatorial plane. Assuming the bar also had the moment of inertia of the rigid spheroid, Weinberg found that in a dense halo, the pattern speed of a strong bar would decay with a half-life of a few of its initial rotation periods.
While the complicated LBK torque expression (Eq. 20) is daunting, its physical meaning is very similar to that of Chandrasekhar's formula (Eq. 29). The drag force arises because, to second order, the halo builds up a density excess, or wake, behind the perturber, leading to a gain, on average, of angular momentum by the halo particles and a corresponding loss by the perturber. The lagging wake was illustrated for the case of a bar by Weinberg & Katz (2007, their Fig. 1).
As Lynden-Bell & Kalnajs (1972) showed for spiral perturbations, halo particles that are not in resonance also experience changes that average to zero and therefore the drag is caused only by resonant particles. Referring back to Eq. (20) again, the contribution to the drag from each resonance depends on the gradient of the halo particle DF across that resonance, and there is generally an excess of gainers over losers. But the gainers will depopulate the high-density side, and cross the resonance to the previously low-density side. Thus, were the pattern speed of the perturber to remain constant, the local gradient across the resonance would be reduced, and the system would adjust toward a balanced equilibrium in which the gradient in the DF in the immediate vicinity of the resonance had flattened. Then the imbalance of gainers over losers would be erased and friction would die away. This effect was explicitly demonstrated by Lin & Tremaine (1983) for the case of an orbiting satellite, and will turn out to be important in Section 6.2.1.
However, the motion of the perturber is affected by its loss of angular momentum. An orbiting mass clearly sinks inward, making its angular speed about the center rise. Because a bar is not a solid object with a well-defined moment of inertia, Tremaine & Weinberg (1984b) were less certain about whether its pattern speed would increase or decrease as a result of angular momentum loss. However, simulations (Sellwood 1980; Debattista & Sellwood 1998, Debattista & Sellwood 2000; Sellwood 2003; Athanassoula 2003; Valenzuela & Klypin 2003; Holley-Bockelmann et al. 2005; Martinez-Valpuesta et al. 2006; Villa-Vargas et al. 2009; Minchev et al. 2012a) have always found that bars slow as they lose angular momentum.
The change in pattern speed of the perturber causes the resonances to sweep through phase space (Sellwood & Debattista 2006; Dubinski et al. 2009), and therefore the gradients across resonances do not have time to flatten and, in general, friction persists as the perturber loses angular momentum, although exceptions have occurred (see Section 6.2.1).
Lin & Tremaine (1983), Bontekoe & van Albada (1987), Arena & Bertin (2007) and Jardel & Sellwood (2009) for an orbiting satellite, and Sellwood (2006) for a rotating bar, showed that the dependence of the friction term on the perturber mass, its angular speed, and both the dispersion and density of the halo, were all as expected from Eq. (29). The inclusion of self-gravity of the halo causes a slightly larger density response, with a corresponding increase in the drag force, but does not appear to change the scaling.
The case of a bar rotating in a halo has received a great deal of recent attention, as friction from a moderately dense halo slows the bar on a time-scale of a few rotations (Sellwood 1980; Weinberg 1985). Bars also grow in length and strength (i.e. the quadrupole moment rises) as they are braked by friction.
While many resonances exist between the bar and halo orbits, Weinberg & Katz (2007) stressed that frictional drag was dominated by a small number of resonances, of which the ILR was by far the most important. The consequence of flattening the gradient in the halo DF at this resonance has also affected simulation results (see Section 6.2.1).
The phase lag angle between the axis of the halo response and principal axis of a bar varies with the drag force (Debattista & Sellwood 2000; Sellwood 2006). Friction is weak at high angular speeds because the halo response is almost exactly perpendicular to the bar, it strengthens as the pattern slows reaching a maximum when the response is ~ 45∘ to the bar axis, and decreases to zero as the response becomes aligned with the bar, which generally happens before the bar is brought to a complete stop. Thus the system reaches a steady state in which the corotating halo response, which has been described as a halo bar (Athanassoula 2007), is aligned with the bar in the disk. Since the response of orbits to a steadily rotating bar potential is a forced precession (see Section 5.1), it is no surprise that studies of halo orbits in barred simulations (Athanassoula 2002, Athanassoula 2003; Ceverino & Klypin 2007) have found a large fraction of resonant orbits.
It is possible that such trapped orbits are responsible for the asymmetric distribution of thick-disk and/or luminous halo stars in the Milky Way. A density excess of such stars that are only a few kiloparsec from the Sun in the first Galactic quadrant, with no counterpart in the fourth quadrant, has been reported most recently by Larsen et al. (2008). A similar asymmetry, that could be aligned with the bar in the disk, was also found by the same group (Parker et al. (2004)) in stellar kinematics.
Debattista & Sellwood (2000) experimented with rotating halos, finding that the frictional drag varies with the degree and sense of halo rotation. It is little changed in halos having mild rotation in the same sense as the disk, and is significantly weakened only by an unrealistic degree of halo rotation.
The loss of angular momentum from the bar to the halo slows the bar and allows it to continue to grow (Debattista & Sellwood 2000). Continued evolution of bars in moderately dense halos (Athanassoula & Misiriotis 2002; Athanassoula 2003; Martinez-Valpuesta et al. 2006) can cause the bar to grow until it fills almost the entire disk, at which point corotation can be outside the disk. The unreasonably large bars, relative to the disk size, obtained in these simulations would appear to argue against even moderately dense inner halos for real galaxy disks.
The halo that absorbs the angular momentum, need not be just the dark matter halo; visible spheroidal components are also angular momentum sinks. Saha et al. (2012) found that an initially nonrotating classical bulge acquires angular momentum from a strong bar and becomes triaxial, corotating with the bar when angular momentum transfer is complete. The bulge streaming motions they report are quite large.
6.2. Constraint on halo density
While the above theory leads to the expectation that a halo must exert
a strong frictional drag on a massive bar, fully self-consistent
simulations were needed to show that a bar in a disk embedded in a
dense halo slows to the point that
> 1.4
(Debattista &
Sellwood 2000;
Weinberg & Katz
2002;
Sellwood 2003;
Valenzuela &
Klypin 2003;
O'Neill & Dubinski
2003;
Holley-Bockelmann
et al. 2005;
Villa-Vargas et
al. 2009),
which is inconsistent with most observed values.
The pattern speeds of strong bars are generally fast, in that
~ 1.2 (Eq. 28); the
evidence is reviewed in Section 5.8.
Furthermore, the slow bar reported by
Chemin & Hernandez
(2009)
is in the low-surface-brightness galaxy UGC 628, which is
believed to have a large DM fraction that should have slowed a strong bar.
The observationally accessible ratio
is not a direct measure
of friction, since both the bar length and corotation radius can
change independently, but halo friction has driven this ratio to a
high value in all collisionless simulations in which a strong bar
rotated in a dense halo. Since no convincing counter-examples of
strong bars in dense halos remaining fast for long periods have been
found (see Section 6.2.1), the simulations clearly
predict low density halos for the majority of strongly barred galaxies. This
result is little changed in simulations with moderate fractions of gas
(Villa-Vargas et
al. 2010),
but friction is weaker because bars are smaller and
weaker in simulations with unreasonably large gas fractions.
Obviously, the magnitude of the friction force varies with bar
strength, and weak bars therefore experience little friction,
e.g. simulation MHH2 by
Athanassoula (2003).
Unfortunately, this author does not give the crucial value of
for any of her
simulations, limiting further interpretation of her many results.
Since strong bars experience fierce braking from moderately dense halos, Debattista & Sellwood (1998, 2000) argued that bars in real galaxies can remain fast only if the central dark matter density is much lower than was predicted by galaxy formation models. The implication of their result led to the conclusion being examined very closely by others, but even though two serious issues were raised (see below), their conclusion still holds.
6.2.1. Anomalously weak friction
Valenzuela & Klypin (2003) reported that the bar in a disk embedded in a cuspy halo rotated at almost its initial speed for quite some time, and did not experience strong braking, which was inconsistent with all other numerical results and with theory! Sellwood & Debattista (2006) reproduced their anomalous result when they reran the exact same model, and were able to show that the reason for the absence of friction stemmed from a flattened gradient in the halo DF at the crucial ILR. While the halo DF had a density gradient ∂ f / ∂ Lz that was negative everywhere initially, the halo DF was changed by interactions with the disk bar as it formed. As the disk bar buckled, its pattern speed increased, with the implication that the resonances returned to parts of phase space where the previous changes at those resonances had flattened the gradient in the DF. Since friction depends upon there being an excess of gainers over losers caused by a decreasing density across the resonance, the absence of a gradient allowed the bar to rotate without friction – exactly as Lin & Tremaine (1983) had shown for a sinking satellite. Strong friction resumed after a while, probably because mild braking at minor resonances eventually moved the ILR resonance into a region where the DF gradient was normal. Sellwood & Debattista (2006) were also able to show that the near-frictionless state was fragile, and could not be expected to arise in nature, since tiny perturbations by passing low-mass satellites were sufficient to shake the halo out of its "meta-stable" state and to cause fierce friction to resume.
This type of behavior was the root cause of the stochastic variations found by Sellwood & Debattista (2009). They reported that the evolution of the bar pattern speed in many different random realizations of the same (isolated) model galaxy varied widely because the halo DF was sculptured by the early disk evolution, which was stochastic. The chance absence of gradients in the DF at the dominant resonance inhibited friction for periods that varied widely from realization to realization. Stochastic behavior was unaffected by changes to the numerical parameters, even the particle number, and persisted when they used a tree code instead of a grid code. Thus a simulation of an isolated galaxy that shows weak friction between a strong bar and a dense halo for a short period (e.g. Klypin et al. 2009) is inconclusive; firm evidence for weak friction that contradicts all the theory and experimental evidence summarized above would require longer simulations that are repeated with different random realizations.
Weinberg & Katz (2007) claimed that simulations require immense numbers of particles to reproduce the correct frictional drag. Their argument stemmed from their recognition that most of the frictional drag arises from the gradient in the halo DF across a single resonance, the ILR. They argued that too few particles in this small region of phase space would prevent the bar from experiencing the correct drag. Their predicted symptoms of this deficiency would be stochastic variations in the drag force resulting from shot noise in the local distribution of particles that happened to be in the vicinity of the resonance. (It should be emphasized that they were discussing friction with an imposed rigid bar, which is separate from the possible stochastic variations due to disk evolution that were discussed in the previous paragraph.) They went on to estimate that simulations needed a hundred-fold increase in the number of particles, from ~ 106 to ~ 108, before this problem would be brought under control.
Sellwood (2008b)
conducted a series of simulations of exactly the kind that
Weinberg & Katz
(2007)
envisaged (a rigid bar in a halo of massive
particles) and found that only very small numbers of particles
(
104)
behaved stochastically in the manner predicted by
Weinberg & Katz
(2007).
Once N 
105, the evolution of both the pattern
speed and the halo mass profile was independent of N, and no new
behavior emerged when the number of particles was increased to
N = 108.
The reason for the discrepancy with the predictions of Weinberg & Katz (2007) is that the resonances are broadened by the time dependence of the bar pattern speed. Their estimates of particle number requirements used only the intrinsic width of the resonance due to the finite amplitude of the perturbation – in effect, they assumed a fixed pattern speed. A much larger fraction of the particles than these authors expected contribute to the friction when the pattern speed decreases rapidly due to frictional drag from the halo, and friction can be reliably reproduced in simulations of strong bars with 105 to 106 halo particles. Ceverino & Klypin (2007) and Dubinski et al. (2009) came to similar conclusions.
As noted in Section 2.1, all collisionless cold dark matter models of halo formation predict a steep inner gradient to the halo density profile, whereas shallower density profiles seem to be required (e.g. Sellwood 2009; Kuzio de Naray & Spekkens 2011). Dynamical friction between the baryons and the dark matter halo has been proposed as a possible solution to this discrepancy.
Weinberg & Katz (2002) and El-Zant et al. (2001) argue that dynamical friction between the halo and bars or gas clumps respectively could transfer enough energy to the dark matter halo to reduce its density in the inner parts of galaxies. Note that the mechanism invoked in these papers is somewhat distinct from galaxy formation models (Read & Gilmore 2005; Governato et al. 2010; Pontzen & Governato 2012) that invoke repeated changes to the gravitational potential as gas disks collect and then evaporate; since this latter mechanism is essentially part of current ideas for galaxy formation, I do not review it here.
6.3.1. Halo density reduction by bars
A number of authors have reported a mild reduction in halo density resulting from bar friction (Hernquist & Weinberg 1992; Debattista & Sellwood 2000; Athanassoula 2003; McMillan & Dehnen 2005), and both Holley-Bockelmann et al. (2005) and Sellwood (2008a) verified that the dominant changes occurred at the ILR. Simulations with rigid bars that are pinned to a center can suffer from a numerical artifact if the halo is allowed to become lop-sided (Sellwood 2003; McMillan & Dehnen 2005), resulting in an erroneously large angular momentum transfer.
A convenient measure of halo density is its mean value inside the
radius where the circular speed has risen to half its peak value
(Alam et al.
2002).
Sellwood (2008a)
found that moderate, rigid bars
reduced this quantity by a few percent, as already noted, but an order
of magnitude reduction required a bar of length ~ 12-20 kpc, an
axis ratio a / b
3, and a
bar mass
30% of the enclosed halo mass. In fact, the angular momentum given up by the
bar in order to achieve this density reduction exceeded the likely
store of angular momentum in a galaxy disk
(McMillan & Dehnen
2005;
Sellwood 2008a).
Furthermore, a real bar, formed say through instabilities in the disk, contracts as it loses angular momentum to the halo, since the sizes of the stellar orbits that make up the bar themselves shrink. The resulting increase in the central attraction causes the halo density to rise, an effect that can overwhelm the density reduction due to angular momentum changes (Sellwood 2003; Colán et al. 2006; Dubinski et al. 2009).
6.3.2. Halo density reduction by moving mass clumps
El-Zant et al. 2001, and later Tonini et al. 2006, proposed that moving clumps of dense gas will also transfer energy to the DM halo through dynamical friction and lower its density. They envisaged that baryons would collect into clumps through the Jeans instability as galaxies are assembled and present somewhat simplified calculations of the consequences of energy loss to the halo through dynamical friction. The dynamical process is that of mass segregation, which is well known in other contexts, such as in globular clusters (e.g. Merritt et al. 2004), but requires much larger mass differences for evolution on an interesting time scale.
The idea has been tested in idealized N-body simulations in which the heavy mass clumps were modeled as softened point masses (e.g. Jardel & Sellwood 2009; Goerdt et al. 2010; Cole et al. 2011). Generally, low-mass clumps were found to be ineffective, because dynamical friction is too weak. However, the orbital decay of a really massive clump, about 1% of the virial mass of the halo, does transfer enough energy to the halo particles to effect a substantial reduction in its density, even as the heavy clump itself deepens the gravitational potential.
Ma & Boylan-Kolchin (2004) used clumps which were themselves composed of particles that could therefore suffer tidal stripping, etc. They reported that the stripped particles remained roughly at the radii at which they were detached, and also found that significant reduction in the halo density was caused by only the heaviest clumps.
The proposed mechanism faces a number of challenges, however. The settling gas clumps are assumed to maintain their coherence for many dynamical crossing times without colliding with other clumps or being disrupted by tidal fields and/or star formation, for example. Romano-Dáaz et al. (2008a) claimed that baryonic physics had precisely this effect in their galaxy formation simulations, but calculations (e.g. Kaufmann et al. 2006) of the masses of the condensing gas clumps suggest they range up to only ~ 106 M⊙, which is too small to experience strong friction. Larger clumps will probably reside in subhalos, which may get dragged in, but simulations with subclumps composed of particles (e.g. Ma & Boylan-Kolchin 2004) indicate that the DM halos of the subclumps will be stripped, and the stripped matter largely replaces any DM moved outwards in the main halo. Thus if dynamical friction is to accentuate the separation of the baryons from dark matter before the baryonic mass clumps in subhalos settle to the center, they must somehow be stripped efficiently of their dark matter without dissolving the gas clumps themselves.
Mashchenko et al. (2006, 2008) argue that the energy input to the halo, mediated by the motion of the mass clumps, can be boosted if the gas is stirred by the usual feedback from stellar winds and supernovae. A challenge for this mechanism is the difficulty of accelerating such massive gas clumps into coherent motion, since the high-pressure material from the postulated energetic events will vent more easily along low-density paths, thereby relieving the pressure before the dense clumps gain much momentum (e.g. MacLow & Ferrara 1999).