


As far as the universe is traced by its large scale mass structures (galaxies, clusters of galaxies, superstructures), the questions asked in observational cosmology are concerned with the angular and in-depth distribution of such structures, their material content, the occurence of chemical elements, the origin of particular objects, as e.g., quasars, or galactic nuclei, the strength and time-evolution of magnetic and radiation fields, etc. In this respect, the highly isotropic microwave background (CMB), a Planck-distribution to temperature ~ 2.7 K, interpreted to be of cosmological significance, is a very important characteristic. From the observations, properties will be ascribed to the universe serving as entries for cosmological model building.
As main result, a compatibility with observations of cosmological significance had been found: the expansion of the universe (redshift), the isotropy of the slices of equal time (CMB), and the "cosmic" abundance of light chemical elements. Isotropy does not refer to the position of the earth, the solar system or the Galaxy but to an imagined rest system defined by CMB itself. Nucleosynthesis calculations lead to a value for the average matter (baryon) density of the universe consistent with what is observed, directly, from luminous masses and, indirectly, through dynamical effects in galaxies and clusters of galaxies depending also on dark matter.
Before a quantitative description of the universe can be attempted, a particular cosmological model, i.e., a metric representing the gravitational potentials, and a description of its material sources, must be given. In order to reach a unique model, a number of simplifying assumptions usually is made. The historical and epistemological background is provided by what often is called the Copernican Principle: "The Earth does not occupy a prefered position in the universe." Expressed differently, some kind of homogeneity of space is demanded. Mathematically, this is expressed by requiring a transitive group of quasi-translations (isometries) to act on spacelike hypersurfaces. This still leaves a sizable number of cosmological models (cf. [45], particularly secs. 12.3, 12.4, and 15.3). Also, the Copernican principle is untestable as long as we cannot observe the universe, say, from another galaxy. It can be tested only along our past lightcone by the counting of sources as a function of redshift. By transforming redshifts (look-back times) into spatial distances, homogeneity of space then may be infered. However, the calculation already must involve a cosmological model.
In order to further reduce the number of cosmological models, the Copernican Principle is replaced by the Cosmological Principle: "The universe must be homogeneous and isotropic." Isotropy means that the rotation group acting on spacelike hypersurfaces is also a symmetry group. This principle leads to a unique class of cosmological models (FLRW, cf. section 3.2). It likewise is not testable from our vantage point in the universe. 12
From the point of view of what is observed (large scale galaxy structure, cosmological background radiation (CMB)), the Cosmological Principle can lead merely to an approximate description of the universe. A large fraction of cosmologists starts with the Cosmological Principle and accounts for the inhomogeneities of the matter distribution and the minuscule anisotropies in CMB by superimposing them onto the model via perturbation calculations. Other cosmologists first apply an averaging over space volumes to the Einstein equations in order to take account of inhomogeneities. Time derivation and averaging over space do not commute. The procedure is called backreaction (of the inhomogenities) and leads to additional terms in the usual (Friedman-) equations for the homogeneous and isotropic model. For applications and a recent review cf. [48]), [49]. Still other researchers directly start from exact inhomogeneous and isotropic solutions of Einstein's equations (collected e.g., in [46]) and try to fit them to the observations. Suggestions also have been made for using the Cosmological Principle only as an initial condition for the development of the Universe [50], or for interpreting it in an average sense ("statistical cosmological principle" [51]).
In the following, we list a few assumptions necessarily leading to a homogeneous and isotropic cosmological model. These assumptions should be testable by their consequences. With better data, they could be relaxed as well.
- A1 The physical laws, in the form in which they are valid here and now, are valid A) everywhere, and B) for all times for which the cosmological model is expected to be valid. Otherwise, it would be impossible to uniquely interpret observations. In theory, it would make no sense to apply the standard model of elementary particles or Einstein's theory of gravitation to the early universe. A1 can also express the hope that local and global physics (of the universe) are not inextricably interwoven: "physics on a small scale determines physics on large scale" [59]. The opposite view that "the physical laws, as we usually state them, already involve the universe as a whole" gets only a minority vote [60].
- A2 The values ascribed to the fundamental constants
here and now are the same everywhere and at all times.
When speaking about fundamental constants, we naively think of
quantities like c (velocity of light), h (Planck's
constant), kb (Boltzmann constant),
e (elementary charge), G (gravitational constant), or of
dimensionless
combinations of them. In order that the atomic spectra from distant
objects can be interpreted, the fine structure constant must be assumed to
be the same as in the laboratory. For a proper interpretation of
gravitational lensing, the gravitational constant must be assumed to be the
same as in the planetary system. Then, by observation, bounds for an
eventual change in the fundamental constants can be obtained, in principle.
Of course, it is the underlying theories which define these quantities
to be constant or time-dependent: In scalar-tensor gravitational theory,
the gravitational "constant" would be time-dependent by definition.
For cosmological modeling in the framework of general relativity,
A2 is to
apply for epochs since, and perhaps including, the inflationary
phase. In elementary particle physics, for higher energies fundamental
constants depend on the renormalization scale. This seems not yet to
play a role for the present cosmological model. Nevertheless, effects
of a running cosmological and gravitational constant on the evolution
of the universe were studied in
[52].
- A3 The universe is connected (in the mathematical sense).
As we know from the occurence of horizons, A3 cannot be sharpened to the demand that communication is possible between any two arbitrarily chosen events in the universe.
- A4 In a continuum model, the material substrate of the universe (including dark matter) is described by a mixture of ideal fluids - not viscous fluids.
- A5 The material substrate of the universe evolves in
time as a laminar flow - not a turbulent one.
The assumption of an ideal fluid without shear and rotation of the
streamlines as expressed by A4, A5
uniquely leads to the FLWR-class of
cosmological models. In A4, an ideal fluid is
characterized by the equation of state p = w
ρ with a constant 1 > w > 0.
13
In fact, as an addition to the current standard cosmological
model, effects of viscosity and turbulence in the course of the
evolution of large-scale structures are being investigated (perturbation
theory), e.g., in connection with dark matter, or dark energy, and
magnetic fields of cosmological relevance, etc.
A5 also expresses the possibility of a slicing of space-time into hypersurfaces of constant time. A fundamental hypothesis going into the standard model is the concept of a cosmic time common to all parts of the universe. In some cosmological models as, for example, in Gödel's, the local spaces of simultaneity are not integrable to one and only one 3-space of "simultaneous being". (Cf. section 3.5.)
3.1.1. Primordial Nucleosynthesis
Primordial nucleosynthesis is considered to form one of the pillars of the standard cosmological model. Nucleosynthesis for the light elements d, 3He,7Li, except for 4He, depends sensitively on a single parameter of cosmological relevance entering: the ratio η = nb / nγ of the number of baryons to the number of photons in the universe. nγ can be calculated from the microwave background. The decisive nuclear physics parameter is the neutron's lifetime. Because the production of 4He depends on the number of existing neutrino families, it is possible to obtain an estimate consistent with what has been found with the largest particle acclerators [72]. Nevertheless, a recent measurement of the 4He abundance "implies the existence of deviations from standart big bang nucleosynthesis" [53].
As to the comparison with observations, except for 4He, for nine reliable determinations of 3He from high redshift quasistellar sources, and for seven reliable determinations of deuterium at high redshifts and low metallicity, the observed distribution of the light elements comes from measurements within the solar system and the Galaxy. The uncertainties are in the range of 0.2% for 4He, 5-10% for d, 3He and 15% for 7Li [56], [57]. There also remains an unexplained difference between the observed and the theoretically calculated values for the abundance of 7Li. From these data a 5% determination of the baryon density is obtained [57]. There are also observations of the chemical abundance in very old stars [58], but their cosmological relevance is not yet clear. In addition to the restricted observation-volume, the empirical basis for the abundance of chemical elements thus is less secure than one might wish it to be. The comparison of calculated and observed abundances depends highly on astrophysical theory (models for the chemical evolution of galaxies and stars).
3.1.2. Empirical situation with regard to A2
All we can safely claim today, with respect to A1 and
A2, is that they
are not in conflict with the empirical data. Reliable such data about a
time dependence of the fundamental constants are still lacking, although
much progress has been made. For the quantity looked at most often, i. e.,
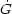 / G,
bounds between |
/ G,
bounds between |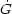 /
G| ≤
10-10 y-1
and |
/
G| ≤
10-10 y-1
and |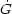 / G|
≤ 10-13 y-1
have been derived from various investigations (solar system, radar
and laser ranging to moon/satellites, astro-seismology, binary pulsar, big
bang nucleosynthesis, Ia supernovae). Cf. the review by García-Berro et al.
([54],
p. 139-157). Most of the estimates are dependent on the cosmological
model. Also, they suffer from short observation spans: measurements in the
solar system cover the past 200 - 300 years
[55].
At best, the observation time could be extended to ~ 109 y,
i.e., the lifetime of the
solar system. Only then would this be comparable to Hubble time
t0 = 1 / H0 ≃ 9,771/h
× 109 y, with H0 = 100 h
km s-1 (Mpc)-1, the Hubble constant measuring
present expansion.
14
The situation is not better for the estimates on
/ G|
≤ 10-13 y-1
have been derived from various investigations (solar system, radar
and laser ranging to moon/satellites, astro-seismology, binary pulsar, big
bang nucleosynthesis, Ia supernovae). Cf. the review by García-Berro et al.
([54],
p. 139-157). Most of the estimates are dependent on the cosmological
model. Also, they suffer from short observation spans: measurements in the
solar system cover the past 200 - 300 years
[55].
At best, the observation time could be extended to ~ 109 y,
i.e., the lifetime of the
solar system. Only then would this be comparable to Hubble time
t0 = 1 / H0 ≃ 9,771/h
× 109 y, with H0 = 100 h
km s-1 (Mpc)-1, the Hubble constant measuring
present expansion.
14
The situation is not better for the estimates on
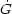 / G made
from primordial nucleosynthesis
(PN) giving a value for the ratio of GPN /
G0 = 0.91 ±
0.07 taken at the time of big bang nucleosynthesis and at
present. For CMB GCMB / G0 = 0.99
± 0.12, i.e., since ~ 3 × 105 years.
[57].
/ G made
from primordial nucleosynthesis
(PN) giving a value for the ratio of GPN /
G0 = 0.91 ±
0.07 taken at the time of big bang nucleosynthesis and at
present. For CMB GCMB / G0 = 0.99
± 0.12, i.e., since ~ 3 × 105 years.
[57].
As to the determination of upper bounds for the fine structure constant α, constraints coming from terrestrial (Oklo natural reactor), high-redshift quasar absorption systems, big bang nucleosynthesis, and the angular spectrum of cosmic background radiation "do not provide any evidence for a variation of α" (cf. [54], p. 139). Typical results are Δα / α = (-0.3 ± 2.0) × 10-15 y-1 (laboratory), Δα / α = (0.05 ± 0.24) × 10-5 (quasars at z = 1.508)), and Δα / α = (-0.054 ± 0.09724) (CMB at z ≃ 103). Another interesting target has been the ratio of proton and electron mass μ = mp / me. A typical bound is |Δμ / μ| = (-5.7 ± 3.8) × 10-5 for redshifts of z = 2.377 and z = 3.0249, respectively. (cf. [54], p. 159).
The time-independence of the fundamental constants which is particularly important in the inflationary phase, is not directly testable during this period.
3.1.3. Cosmological observation
In addition to fundamental suppositions for theoretical modeling, hypotheses for the gaining of data and the empirical testing of cosmological models are necessary. Such are, for example:
- B1 The volume (spatial, angular) covered by present observation is a typical volume of the universe.
The application of B1 may become problematic because of the occurence of horizons in many of the cosmological models used. There may be parts of the universe not yet observable (particle horizons) or parts which, in principle, cannot be oberserved from our position.
An example for observations n o t satisfying B1 is formed by the sample used for gaining and calibrating spectra of Ia supernovae [61].
- B2 Observation time is long enough in order to guarantee reliable data of cosmological relevance.
- B3 Ambiguities in observation and theoretical interpretation (selection effects) are identified and taken into account by bias parameters.
An example for a bias parameter b(z, k) is given by the expression for the observable galaxy overdensity δg as a measure of the underlying (average) matter density δm: δg = b(z, k) δm ([62], eq. (3)). It is unclear whether these demands on observation are satisfied, at present. In particular, selection bias concerning luminous objects may be underestimated ([64], p. 321).
But it is in observation that tremendous progress has been made in the past two decades. 3-dimensional redshift surveys of galaxies 15 have been much extended. In particular, this was done by the 2dF galaxy redshift survey (combined with the 2QZ quasar redshift survey) (2003): patches of 2 × 2 degrees have been probed and 221414 galaxies (23424 quasars) measured out to 4 ⋅ 109 lightyears (up to z = 0.22) (2QZ: two 5 × 75 degree stripes both in the northern and southern sky) (http://www2.aao.gov.au/2dfgrs/). Most impressive is the Sloan digital sky survey [65], [66]: it comprises ~ 106 galaxies, with the subsample of luminous red galaxies at a mean redshift z = 0.35 and 19 quasars at redshifts z ≥ 5.7 up to z = 6.42 (http://www.sdss.org). Cf. also the "Union Sample" of Ia supernovae containing 57 objects with redshifts 0.015 < z < 0.15 , and 250 objects with high redshift [67]. In view of an assumed total of ~ 1011 galaxies in the universe and the fact that angular position surveys extend only to depths of a fraction of the Hubble length, one cannot say that these surveys are exhaustive. Moreover, in view of the fact that estimates of the mass-luminosity ratio lead to Ωlum ≃ 0.005 for the relative density of luminous matter, the cosmological relevance of the galaxy surveys is questionable; they may amount only to a consistency check. The scale of homogeneity for which averaging of the observed large structures (superclusters, voids) is reasonable, has steadily increased in the past and could grow further, in the future. At present, the size of the Great Wall, i.e., ≃ 400 Mpc seems to point to a homogeneity scale of ≥ 100 Mpc [68]. The surveys described have been used to test homogeneity, e.g., by counts of luminous sources in a redshift range of 0.2 < z < 0.36, albeit with distance calculations within the homogeneous and isotropic ΛCDM-model [69].
Isotropy with respect to our observing position also has been put to a test; a statistically significant violation of isotropy for Ia supernovae at redshift z < 0.2 and refering to deviation in the Hubble diagram (Northern and Southern Hemispheres) has been found [70]. Problems related to observations were investigated carefully by G. F. R. Ellis [71], [7].
3.2. More on the standard cosmological model
In the standard model, the gravitational field and space-time are described by a (pseudo-)Riemannian manifold with a homogeneous and isotropic Lorentz metric. It is an expression of the Cosmological Principle, which alternatively can be formulated as (cf. section 3.1): "No matter particle (of the averaged out ideal cosmic matter) has a prefered position or moves in a prefered direction in the universe". Consequently, the space sections of the spacetime manifold describing the universe are homogeneous and isotropic in the sense of an average (on the largest scales) over the observed matter distribution. The cosmological metric (gravitational potentials) is given by a Friedman-Lemaitre-Robertson-Walker solution (FLRW) of Einstein's field equations - with or without cosmological constant. The metric depends on a single free function a(t) of cosmic time and allows for a choice among three space sections with constant 3-curvature (k = 0, +1, -1). The parameter k is related to the critical energy density ρc = 3c4 H02 / 8π G such that k = 0 for ρ = ρc; k > 0 for ρ > ρc and k < 0 for ρ < ρc. This follows from the Friedman equations. When formulated with dimensionless (energy-) density parameters Ωx: = ρx / ρc, where the index x stands for c (critical-), d (dark-), b (baryonic-), t (total matter), respectively, and ρΛ = Λ c4 / 8π G, ρk = k c4 / 8π G a(t)2, one of the two Friedman equations reads (trivially, Ωc = 1):
 |
(1) |
with Ωt = Ωb + Ωd + Ωradiation. Due to its smallness, we mostly will neglect Ωradiation = Ωγ(1 + 0.2271 Neff) with Ωγ the photon density and Neff the (effective) number of neutrino species ([84], p. 335).
The space sections for k = +1 are compact; those for k = 0, -1 usally are called "open" as if they could have only infinite volume. This misconception is perpetuated in otherwise excellent presentations of cosmology; in contradistinction, a sizeable number of space forms of negative curvature with finite volume were known to mathematicians since many years (cf. [20], [73], p. 405). This is important because different topologies can be consistent with the WMAP-data [74].
The lumpiness of matter in the form of galaxies, clusters of galaxies, and superstructures is played down in favour of a continuum model of smeared out freely falling matter like in an ideal gas. Its particles follow timelike (or lightlike) geodesics of the FLRW-metric. Inhomogeneity then is reintroduced through linear perturbation theory on this idealized background. In two stages in the history of the universe, both with power-law expansion, the equation of state considered above refer to pressureless matter (baryon dominated universe) and to radiation where p = 1/3 ρ (radiation dominated universe). 16 At present, a general equation of state p = wρ, with w being allowed to be negative, is deemed necessary because the cosmological constant may be simulated by p = -ρ.
Moreover, from observations alone, it seems unclear whether it is possible to discriminate, in our neighborhood, between a Friedman model and spatially inhomogeneous models centered around our position and resembling a Friedman model (Lemaitre-Tolman-Bondi- or Stephani exact solutions). For a review cf. section 2.3 of [76]. Also, a metric combining the FLRW-model and "a perturbed Newtonian setting" has been used to approximately describe features of both the local universe and its large-scale structure [77].
The FLRW-metric describing the cosmological model does not care whether its primordial states are warm or cold. Only when the vanishing of the divergence of the energy-momentum tensor of matter is interpreted as describing the first law of non-relativistic thermodynamics, the expansion of the universe can be seen as an adiabatic process, with the ensuing decline of temperature following the expansion of space. In consequence, it is possible to interpret the microwave background as a relic of an early, hot state of the universe. On the other hand, adiabaticity is violated at the end of the inflationary period where particles and heat are generated. From local physical processes we expect the entropy of the universe to grow with the expansion (deviation from homogeneity). In principle, statistical mechanics (kinetic theory) is the only way for defining properly the concepts of temperature and entropy of the universe: no "external" heat bath is available. Whether they make sense depends on the existence of an unambiguous procedure for coarse graining in phase space. For the entropy concept, cf. the point of view of a strong supporter ([35], section 27).
Mathematically, the most important consequence of the FLRW-models is that they show the occurence of infinite density - as well as a metrical singularity appearing in the finite past: the famous big bang. By mathematical theorems of Penrose and Hawking [14], singularities receive a generic geometric significance within cosmological model building. Their physical aspects were studied by Belinskii & Khalatnikov ([15], [16]). From the point of view of observational cosmology, the infinities connected with the big bang cannot and need not be taken seriously.
We have seen in section 2.1.1 that the "predictive" power of the standard cosmological model is nothing more than an expression of self-consistency. By use of the cosmological model, from the temperature at one past time, e.g., at the decoupling of radiation and matter Tdec, the present background photon temperature would be calculated to be Tphot(0) = Tdec / 1 + z and the baryon temperature Tbary(0) = Tdec / (1 + z)2. The temperature of the neutrino background then is fixed. The consistency problem comes up because Tdec can be calculated via the Saha equation which includes η = nb / nγ, a number which can be read off from the CMB. Of course, this single chain of arguments is supported consistently by others; e.g., the fluctuations in mass density at decoupling must be such that their growth (gravitational instability) until now is consistent with the observed relative anisotropies of 10-5 in the otherwise isotropic CMB etc. As in other parts of physics, there is a net of theoretical conclusions relating empirical data and theory.
The standard cosmological model faced the task of getting away from the homogeneity and isotropy of the averaged out large scale matter content in order to arrive at an explanation of the large scale structures consistent with the required time periods. The hypothesis of primordial adiabatic Gaußian density fluctuations with a nearly scale-invariant spectrum together with various competing scenarios as cold or hot dark matter (in the form of weakly interacting particles), cold baryon matter, cosmic string perturbations, local explosions etc, for some years had not been consistent with the full range of extragalactic phenomena [78], [79], [80]. By now, this debate seems to be ended: the cold dark matter scenario is accepted.
3.3. The concordance model of the universe (ΛCDM)
Due to the observations pointing to an accelerated expansion 17 of the universe in the present era, and due to much progress in astrophysical structure formation theory, the standard cosmological model of the early 90s took the following turn: (1) In structure formation, cold dark matter, i.e., non-relativistic particles subject to gravity, and able to contribute to the growth of matter inhomogeneities (against radiation drag) better than and before baryons can do so, came to play a decisive role; (2) the space sections of the FLRW cosmological model were assumed to be flat (k = 0); (3) the cosmological constant Λ ≠ 0 mimicking a constant energy density became re-installed. A consequence was that due to Ωk = 0 in the Friedman equation (1): Ωt + ΩΛ = 1. Because Ωt contains both, baryonic and dark matter, and due to Ωm = Ωb + Ωd ≃ 0.25, a missing mass ΩΛ ≃ 0.75 resulted, named "dark energy" [81]. This naming occured due to the original interpretation of the cosmological constant as a representation of "vaccum energy" in the sense of the energy of fluctuations of quantum fields (cf. the end of 3.5).
Observation of the luminous-galaxy large-scale-structure also showing baryonic acoustic oscillations (BAO), of the temperature anisotropies of the cosmic backgound radiation (CMB) as well as the determination of the value of the Hubble constant, and the age of the universe, all have been used to support the ΛCDM model. In particular, CMB measurements by the WMAP (Wilkinson Microwave Anisotropy Probe)-satellite as reflected in the acoustic peaks from baryonic and dark matter give information on ([82], table 7, p. 45):
- the geometry of space sections (→ k small, -0.0179 <
Ωk < 0.0081);
- matter energy density Ωm =Ωb +
Ωd ~ 0.258± 0.03;
- vacuum energy density ΩΛ ~ 0.726 ±
0.015;
- baryon density Ωb ~ 0.0456 ± 0.0015;
as well as about further cosmological parameters:
- cold dark matter density Ωd = 0.228 ± 0.013;
- tilt n = 0.960 ± 0.013 of the initial power spectrum
Pinitial ~
 n where
n where
 is the
wave number of the initial fluctuations,
18
is the
wave number of the initial fluctuations,
18
- the Hubble constant H0 = 70.5 ± 1.3 km
s-1 (Mpc)-1.
All these results are based on the CDM model for structure formation.
Two further numbers w0, wz
parametrize a generalized equation of state
p = w(z)ρ, with w(z)=
w0 + z / (1 + z) wz
being allowed to become redshift-dependent
[83].
A "minimal" parameter base of the
ΛCDM model is given by Ωm,
Ωc,ΩΛ, τ,
Δ 2, n where τ = 0.084 ± 0.016 is the optical depth due
to reionization (electron scattering)
[84].
A 7-parameter model with Ωm, Ωb,
Ωd, w0, wa,
h, n is considered in
[62].
The errors in Ωd, Ωb, and the
Hubble constant are claimed to be 3%
([82],
p. 2-3). From WMAP, the baryon accoustic peaks and supernovae, a bound
on the summed neutrino masses mν (of the standard
model of elementary particles) has been
deduced: Σmν ≤ 0.62 eV
[63].
Eventually, this will be confronted with precise measurements of the
neutrino masses on Earth.
2, n where τ = 0.084 ± 0.016 is the optical depth due
to reionization (electron scattering)
[84].
A 7-parameter model with Ωm, Ωb,
Ωd, w0, wa,
h, n is considered in
[62].
The errors in Ωd, Ωb, and the
Hubble constant are claimed to be 3%
([82],
p. 2-3). From WMAP, the baryon accoustic peaks and supernovae, a bound
on the summed neutrino masses mν (of the standard
model of elementary particles) has been
deduced: Σmν ≤ 0.62 eV
[63].
Eventually, this will be confronted with precise measurements of the
neutrino masses on Earth.
3.4. Matter content of unknown origin
From observation of the bulk motion of galaxies and clusters of galaxies in the past 65 years, it is known that more mass than that of the luminous objects must be present. This is needed for an understanding of the dynamics of such objects, for galaxy formation, and for the interpretation of the results of weak gravitational lensing from clusters of galaxies. The mass is missing in and around galaxies (halos). For a review cf. [86]. As we know from section 3.3, baryons, mostly in the form of gas, contribute to only ca. 4%-5% of the relative critical density Ωc = 1 ([4], p. 90). Besides being required to provide an enhancement of gravity, dark matter is assumed to be "non-interacting", i.e., pressureless, otherwise. Computer simulations like the Aquarius Project [87] or MS-II have excellently taken into account and reproduced dark matter: "from halos similar to those hosting Local Group dwarf spheroidal galaxies to halos corresponding to the richest galaxy clusters" ([88], abstract).
For a tentative explanation of dark matter either new cold (i. e., non-relativistic) particles (WIMPs, 19 axions, neutralinos or other light supersymmetric particles, primordial black holes), as well as Q-balls, and other unobserved exotic objects were suggested. The composition of dark matter particles is closely bound to baryogenesis [89]. Eventually, dark matter particles must be found in accelerator-experiments, and their masses measured, in order that their existence be more than speculative. Alternatively, new theories of gravitation have been suggested removing the need for dark matter, as are Modified Newtonian Dynamics (MOND) (cf. [92], Scalar-vector-tensor-gravity (STVG) [93], translational gauge theory [94], [95], etc. Up to now, none of the particles invoked were seen, and none of the alternative theories were able to replace Newtonian theory in all aspects. From the modeling of galaxy formation, hot dark matter in the form of neutrinos seems to be excluded.
Since about a decade, observation of the luminosity-redshift relation of type Ia supernovae has been interpreted as pointing to an accelerated expansion of the cosmos [96], [97]. The simplest explanation is provided by a non-vanishing cosmological constant Λ within the standard cosmological model. In this case, dark energy would be distributed evenly everywhere in the cosmos. It apparently has not played a significant role at early times although reliable knowledge beyond z = 1 is not available ([102], p. 8).
Besides the cosmological constant, tentative dynamical explanations have been given for cosmic acceleration. There, the main divide is between those keeping Einstein gravity or proposing alternative theories. In the first group, we find, on the matter side,
- a new scalar field Φ, named quintessence. Strictly speaking, "quintessence" stands for a number of model theories for the scalar field like cosmic inflation stands for a large number of different models. 20 Quintessence models work with an equation of state w = p / ρ with -1 < w < -1/3. The kinetic energy term is the usual ∇iΦ ∇iΦ while for an extended set of models, i.e., k-essence theories, the kinetic term may read as f(∇iΦ ∇iΦ) g(Φ) with arbitrary functions f, g. In both sets of theories, the scalar field can interact with baryonic and/or dark matter. There are even more speculative approaches taking the kinetic energy terms to be negative (phantom fields) [100]. For further alternative theories of gravitation, cf. the reviews about the understanding and consequences of cosmic acceleration by [76], [101] and [102]. Within Einstein gravity, another road has also been taken:
- By a suitable averaging procedure. It is argued that the differences in gravity between observers in bound systems (e.g., galaxies), and volume-averaged comoving locations within voids (underdense regions) in expanding space can be so large as to significantly affect the parameters of the effective homogeneous and isotropic cosmological model [103]. A great deal of research is available [104], [49], and has lead to testable consequences [105]. The observations seem not yet conclusive with regard to whether we are located in such an underdense void of an extension 200-300 Mpc [106].
If we refrain from accepting proposed ad-hoc-changes of the Friedman equations, among the theories suggested as replacements of Einstein gravity there are theories with higher-order field equations. 21 In one class, the curvature scalar R is replaced by an arbitrary function f(R). For a general review cf. [107]; for a critical status report [108]. Again, scalar-vector-tensor theories of gravitation and vector-tensor theories [109] were put forward. In "make-believe cosmology" models with a higher number of spacelike dimensions are considered, e.g., five-dimensional braneworld models and also string related theories. Cf. section 5.3.
In comparison with dark matter, the observational status of dark energy remains less secure. Observed is a dimming of the luminosities of type Ia supernovae from the luminosity-distance relationship. Together with the homogeneity assumption this leads to acceleration ([76], p. 17, [85]). With further assumptions added, e.g., of flat space sections, dark energy then is reached. At present, the only promising method for its future empirical grounding seems to be (statistical) weak lensing. In contrast, for dark matter the case is very strong, cf. [110], [86].
3.5. Further conceptual pecularities of the standard model
As discussed in section 2, the standard model of cosmology is not free from epistemological and methodological problems. To list one more: Newton's absolute space appears in disguise in the form of an absolute reference system. In particular, (absolute) cosmic time or era is without operational background: the only clock measuring it is the universe itself. By definition, cosmic time is identified with atomic time. By what sequence of clocks the measured time intervals of which must be overlapping, can precise time keeping be realized for the full age of the universe? In particular, which "clocks" to use before structure formation, before nucleosynthesis, before baryogenesis, during the inflationary phase? From the radiocarbon method we know that "radiocarbon years" must be recalibrated to correspond to "calendar years". Such a re-calibration (in terms of radioactivity- and astronomical clocks etc) is necessary also for cosmological time. In the very early universe described by quantum cosmology, only some sort of "internal" time seems to be possible.
Also, there is no operational way of introducing simultaneity. The local method of signaling with light cannot be carried out, in practice, if distances of millions of light years are involved and the geometry in between the large masses is uncertain. It cannot be used, in principle, for the full volume of space if event horizons are present. The cosmological models containing the concept of "simultaneous being of part of the universe" (technically, the space sections or 3-spaces of equal times) are catering to past pre-relativistic needs. For the relativistic space-time concept, access to the universe is gained through the totality of events on and within our past light cone. Hence, "simultaneous being" must be replaced by "what may be experienced at an instant at one place" (a stacking of light cones). Some of the objects at the sky, the radiation of which we observe today, may not exist anymore.
A special case of the hierarchy problem, i.e., the so-called cosmological constant problem, arises if the cosmological constant Λ is not seen as just an additional parameter of classical gravity, but interpreted as the contribution by vacuum fluctuations of quantum field theory. In this case, its value should be immensely larger than the value derived from observations by a factor of ~ 1060 (in theories with supersymmetry), or ~ 10120 (no supersymmetry). In [111] a solution to this problem within quantum gravity has been suggested.
12 Homogeneity follows if the universe is isotropic around more than one point in a spacelike hypersurface, cf. [47]. It is surprising that authors think that "homogeneity on large scales is an extremely strong prediction of ΛCDM" ([69], p. 2) whereas this homogeneity is built into the ΛCDM-model as one of its fundamental assumptions. Back.
13 Here, p is the pressure and ρ the energy density of the ideal fluid. Both, the constancy of w and the range of values allowed will be relaxed. Back.
14 The
Hubble constant is the present value of the Hubble parameter
H(t) :=  / a where a(t) is the scale function of the
homogeneous and isotropic universe model. The dot means time derivation.
Back.
/ a where a(t) is the scale function of the
homogeneous and isotropic universe model. The dot means time derivation.
Back.
15 redshift z = (λ' - λ) / λ directly relates to distance D; for small distances, z = H0D. Back.
16 At redshift z ~ 3600, the period of matter domination follows the radiation-dominated one; decoupling of photons is set at z ~ 1100. For a detailed discussion of the standard model and the early universe cf. [75] or [13]. Back.
17 The so-called deceleration
parameter is defined by q = - (a
 ) /
) /
 2.
Negative q means acceleration.
Back.
2.
Negative q means acceleration.
Back.
18 In fact, the amplitude of curvature
fluctuations is defined by
Δ (
( )2 :=
Δ
)2 :=
Δ (
( 0)2
(
0)2
( /
k0)n(
/
k0)n( 0)
-1+(1/2) dn/dln(
0)
-1+(1/2) dn/dln( ) if n is allowed to
vary.
) if n is allowed to
vary.  0 = 0.002
Mpc-1.
Back.
0 = 0.002
Mpc-1.
Back.
19 Weakly interacting particles. Back.
20 In a specific model, the scalar field has been named "cosmon" [98]. Another suggestion leads to a pseudo-Nambu-Goldstome boson [99]. Back.
21 That is, with Lagrangians of higher-order in the curvature tensor. Back.