


We have seen that the characteristic mass of objects that form from the runaway gravitational collapse of gas, stars and in extreme cases black holes, depends critically on the temperature of the collapsing gas. The hotter the gas, the larger the Jeans mass and the higher the rate at which gas accretes onto the collapsed object. Therefore, the injection of heavy elements by the first supernovae represents a fundamental transition in star formation, in that new coolants are added to the primordial gas. As a result, the characteristic mass of stars formed from the first metal-enriched gas is likely to be lower than the characteristic mass of primordial stars. Here, we investigate the transition between these two modes of star formation.
3.1. The First Supernovae and Metal Enrichment
It is one of the hallmark predictions of modern cosmology that the first heavy elements, such as carbon, oxygen, and iron, are produced in the cores of stars and in supernovae, rather than in the Big Bang (e.g. Burbidge et al. 1957). Thus, when the first stars explode as supernovae the first metals, forged in their cores, are violently ejected into the primordial gas. In this, the first supernovae introduce not just new chemical elements, but also tremendous amounts of mechanical energy that disrupt their environments. Indeed, as given in Section 1, the definition that we have chosen for the first galaxies pertains to this: in the first galaxies, formed in haloes with virial temperatures Tvir ≃ 104 K, the gas can not be completely expelled by a single powerful supernova, as is the case in the minihalos hosting the first stars (see e.g. Bromm et al. 2003; Kitayama & Yoshida 2005; Greif et al. 2007; Whalen et al. 2008).
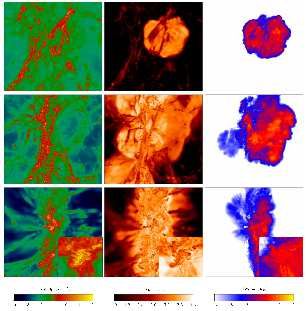 |
Figure 10. The evolution of the remnant of a powerful Pop III.1 supernova, exploding in a minihalo at z ∼ 20. From left to right: the number density, temperature, and metallicity of the gas along the line of sight. From top to bottom: a time series showing the simulation 15, 100, and 300 Myr after the SN explosion. Each panel is 100 comoving kpc on a side, while the inlays show the central 10 comoving kpc. The metals are initially distributed by the bulk motion of the SN remnant, and later by turbulent motions induced by photoheating from other stars and the re-collapse of the shocked gas. As can be seen in the inlays, the gas collapses to high densities once again in an atomic cooling halo in which a first galaxy later forms from the enriched gas. From Greif et al. (2010). |
The effects of a powerful Pop III.1 supernova on the primordial gas are shown in Figure 10, as gleaned from the cosmological simulation presented in Greif et al. (2010). Consistent with the results presented in Figure 1, the gas within the minihalo hosting the progenitor Pop III star is completely blown out into the surrounding IGM. There the primordial gas is shock-heated to several thousand Kelvin and enriched to metallicities of up to ∼ 10−3 Z⊙ within of the order of 107 yr. The evolution of the supernova remnant can be well described analytically, as it passes through the four distinct phases of an explosion with energy ESN = 1052 erg in a medium with particle number density n ≤ 1 cm−3, as expected for a Pop III.1 progenitor star with a mass of the order of 100 M⊙ (e.g. Fryer et al. 2001; Heger & Woosley 2002; Whalen et al. 2008). At first, the blast wave from the supernova propagates outwards at a roughly constant velocity vsh; in this, the so-called free expansion phase, the distance rsh which the shock has traveled from the site of the explosion by time tsh is given simply by
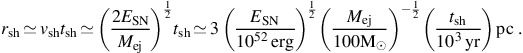 |
(34) |
At this stage all of the energy of the supernova is in the kinetic energy of the ejecta, which has an initial mass Mej. When the shock has swept up an amount of mass comparable to the original ejecta mass, the shock enters the so-called Sedov-Taylor phase in which the energy of the blast wave is conserved while an increasing amount of mass Msw is swept up by the shock. In this phase we therefore have vsh = drsh / dtsh ≃ (2ESN / Msw)1/2, which yields for the shock radius
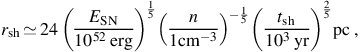 |
(35) |
where we have used Msw = 4π / 3rsh3 µmh n, with µ = 0.6, which is appropriate for an ionized primordial gas. The transition between the free expansion and Sedov-Taylor phase is evident in Figure 11, which charts the propagation of the blast wave of a powerful 1052 erg primordial supernova in a simulated cosmological minihalo, similar to that shown in Figure 10.
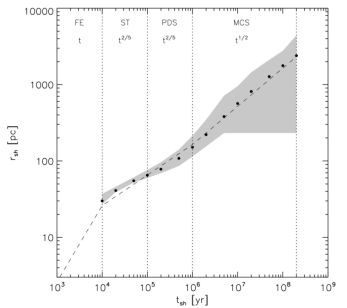 |
Figure 11. The evolution of the remnant of a 1052 erg Pop III.1 supernova in a cosmological minihalo. The analytical solution (dashed lines) discussed in Section 3.1 accurately describes the expansion of the blast wave, the mass-weighted extent of which is shown by the black dots. As the results shown here are from a cosmological simulation, the inhomogeneous density field into which the shock propagates leads to some dispersion in the distance that it extends in different directions (gray region). As shown in Figure 10 for a similar cosmological simulation, after of the order of 108 yr the supernova shock stalls and the metal-enriched gas recollapses into the growing halo which hosted the progenitor star. From Greif et al. (2007). |
The third phase, also shown in Figure 11, sets in when a substantial fraction of the original energy in the blast wave has been radiated away, principally by recombination and resonance line cooling of the hydrogen and helium composing the primordial gas (Greif et al. 2007; Whalen et al. 2008), but also to some extent by bremsstrahlung and inverse Compton scattering of the CMB by free electrons, the latter being most important at high redshift due to the steep increase of the energy density of the CMB with redshift (e.g. Oh 2001>). Known as the pressure-driven snowplow phase, at this stage the high pressure gas behind the blast wave powers its expansion, and the equation of motion thus becomes
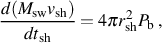 |
(36) |
where Pb is the pressure in the hot bubble interior to the blast wave. As discussed in Greif et al. (2007), at the radius where the transition to the snowplow phase begins, the density profile of the gas is close to that of an isothermal gas, n ∝ rsh−2; within this radius, the density profile is much flatter due to the strong photoheating of the gas by the progenitor star (e.g. Kitayama & Yoshida 2005; and Whalen et al. 2008). Therefore, as the pressurized bubble expands adiabatically, in the snowplow phase we have Msw ∝ rsh and Pb ∝ rsh−5. This, in turn, allows a solution to the equation of motion with rsh ∝ tsh2/5, just as in the previous Sedov-Taylor phase.
The final transition occurs when the bubble behind the blast wave has cooled and the pressure behind the shock no longer affects it dynamically. While by this time a large fraction of the energy of the supernova has been radiated away, the momentum that has accumulated in the dense shell of gas that forms behind the shock is conserved. As the density profile of the ambient gas is still n ∝ r−2 at this point, the conservation of momentum implies that the quantity Msw vsh ∝ rsh drsh / dtsh is a constant. Thus, in this final phase of the supernova remnant rsh ∝ tsh1/2, as shown in Figure 11.
The explosion of a Pop III.1 star with a mass of ∼ 200 M⊙ as is shown Figures 10 and 11, is expected to release up to 1053 erg as well as all of the up to ∼ 100 M⊙ in metals produced in the core of the star (e.g. Heger & Woosley 2002; Heger et al. 2003; Karlsson et al. 2011). The metal-enriched gas that is ejected into the IGM by the supernova explosion expands preferentially into low density regions, as shown in the middle row of panels in Figure 10. This can be seen more explicitly in Figure 12, which shows the metallicity distribution of the gas enriched by a similar primordial supernova as a function of density and temperature (Wise & Abel 2008).
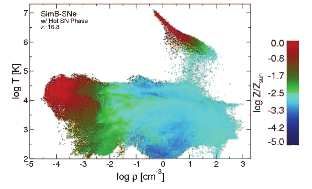 |
Figure 12. The metallicity of the gas enriched by the violent expulsion of metals in a powerful Pop III.1 supernova, similar to that shown in Figures 10 and 11, as a function of the density and temperature of the gas. The highest metallicity gas is in the low density regions into which the blast wave propagates most rapidly. As also shown in Figure 10, the metallicity of the higher density gas re-collapsing into the halo hosting the progenitor star is Z ∼ 10−3 Z⊙. From Wise & Abel (2008). |
The dark matter in the halo hosting the progenitor star is not nearly so violently disrupted as is the gas swept up in the blast wave, and in fact the host halo continues growing until its gravity is strong enough for the cooling, metal-enriched gas to collapse into it again. As shown in the bottom panels in Figure 10, this occurs when the host halo has grown massive enough to host a first galaxy, as the gas is shock-heated to a temperature of ∼ 104 K at the virial radius rvir ∼ 1 physical kpc from the center of the ∼ 108 M⊙ halo. As shown in both Figures 10 and 12, the metallicity of the gas that re-collapses into the growing host halo is typically ∼ 10−3 Z⊙. Therefore, it is expected that stars formed in first galaxies enriched by powerful Pop III.1 supernovae are likely enriched to this level (e.g. Karlsson et al. 2008; Greif et al. 2010; Wise et al. 2011). Such stars would be the first Pop II stars, and as we shall see many of these stars may still be present today, 13 Gyr after the formation of the first galaxies.
3.2. The Mixing of Metals with the Primordial Gas
Here we consider two distinct situations in which the metal-enriched ejecta of primordial supernovae mix with the primordial gas, drawing on the results of the cosmological simluations of Pop III supernovae discussed in Section 3.1. Firstly, we shall estimate the timescale on which the primordial gas in the IGM that is swept up by the blast wave becomes mixed with the ejecta. Then we will turn to consider the likelihood that the primordial gas in minihalos that are overrun by the blast wave is mixed with the ejecta, thereby precluding Pop III star formation in those halos.
When the supernova shock finally stalls after ∼ 108 yr, the dense shell of swept-up gas is accelerated towards the growing halo embedded in the underdense shocked gas. Such a configuration is Rayleigh-Taylor unstable and small perturbations of the shell can quickly grow, leading to mixing of the primordial gas in the shell with the metal-enriched gas in the interior. As a stability analysis shows, a small perturbation on a length scale є << lsh, where lsh is the thickness of the dense shell, will grow exponentially, at a rate
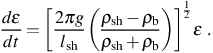 |
(37) |
Here g is the acceleration of the dense shell in the direction of its interior, and ρsh and ρb are the densities of the shell and the interior metal-enriched bubble, respectively. Assuming that ρsh >> ρb, we can estimate the timescale on which the perturbation will grow as (e.g. Madau et al. 2001)
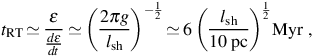 |
(38) |
where in the last expression the gravitational acceleration towards the growing host halo is taken to be g ≃ G Mh / rsh2, with Mh = 108 M⊙, roughly the mass to which the host halo grows during the expansion of the blast wave. We have also used rsh = 3 kpc, which is roughly the spatial extent of the supernova shock when it finally stalls (e.g. Greif et al. 2007). Even for a shell as thick as ∼ 100 pc, the timescale on which the metal-enriched interior material mixes with the ∼ 105 M⊙ of primordial gas swept up by the blast wave is much shorter than the timescale on which the gas re-collapses into the host halo, which is ∼ 108 yr. Therefore, the gas which re-collapses into the host halo is expected to be well-mixed with the metals ejected in the supernova explosion.
While it is thus apparent that the low density gas swept up in the IGM can be efficiently mixed with the metal-enriched material ejected in Pop III supernovae, the blast waves from these powerful explosions can also impact the more dense primordial gas inside neighboring minihalos. It is therefore another key question whether the metals are also mixed with this dense gas, as if so then when it collapses metal-enriched Pop II stars may form instead of Pop III stars. In this case of a supernova blast wave overtaking a dense cloud of self-gravitating gas in a minihalo, there is the possibility of the dense gas becoming Kelvin-Helmholtz unstable, in which case vortices develop at the boundary with the fast-moving metal-enriched gas, and the two will mix with one another. However, for this to occur the dense gas cloud must not be too tightly bound by gravity. In particular, for a given relative velocity between the minihalo and the blast wave, which we can take to be vsh, the gas will be mixed due to the Kelvin-Helmholtz instability at the virial radius rvir of the halo, if (e.g. Murray et al. 1993; Cen & Riquelme 2008)
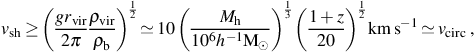 |
(39) |
where for the second expression we have used g = G Mh / rvir2 and we have assumed a density contrast between the gas at the virial radius and that of the shock ρvir / ρb = 10, consistent with the results of the cosmological simulations of Pop III supernvovae shown in Section 3.1. Thus, we see that the gas near the virial radius will be mixed if the speed of the shock exceeds the circular velocity vcirc of the halo, which is likely the case for a minihalo with mass Mh ∼ 106 M⊙ at z ≤ 20.
However, as it is generally the dense gas embedded more deeply in the halo from which stars form, the metal-enriched gas may have to be propagating at a significantly higher velocity in order to impact the nature of star formation in the halo. To estimate how fast the shock must be in order to mix the gas a distance r from the center of the halo, we can take it that the gas in the halo has a density profile that is roughly isothermal, with ρ ≃ ρvir (r / rvir)−2. Using the same rough scaling also for the dark matter, we substitute ρ for ρvir and r for rvir in equation (39) to arrive at the following expression for the shock speed required for mixing via the Kelvin-Helmholtz instability:
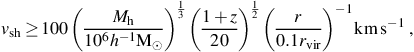 |
(40) |
where we have implicitly assumed the same constant ρb as in equation (39). Therefore, we see that it is only relatively fast shocks that are able to efficiently mix the metal-enriched material with the dense, pristine gas in the interior of a primordial minihalo. The results of this analysis are in basic agreement with the results of simulations of high velocity shocks impacting minihalos, as shown in Figure 13 (Cen & Riquelme 2008).
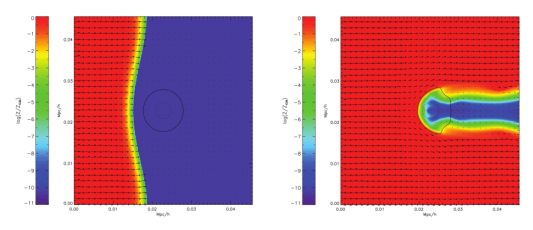 |
Figure 13. The mixing of the primordial gas within a halo with mass Mh = 107 M⊙ with metal-enriched gas overtaking the halo at a velocity vsh = 30 km s−1. Shown is the metallicity of the gas at z = 9 (left panel) and later at z = 6 (right panel). The velocity field, along with contours of ρ = ρvir (solid lines), is depicted in each of the panels. The primordial gas is well-mixed with the metal-enriched gas at radii r ≥ rvir, and is mixed to a lesser degree at smaller radii, in basic agreement with equation (40). Note that the most dense gas in the center of the halo remains pristine; as it is from this gas that stars would most likely form, such a halo is likely to host Pop III star formation, despite being overtaken by high velocity metal-enriched gas. From Cen & Riquelme (2008). |
To gauge the likelihood that a cosmological minihalo is indeed impacted by a Pop III supernova shock that is sufficiently strong to enrich the material in its central regions, we turn to Figure 14, which shows the average distance between Pop III star-forming minihalos in a cosmological simulation of the formation of a halo similar to that of the Milky Way (Gao et al. 2010). This Figure shows that due to the clustering of such halos, the average distance between them is smaller than would be expected from a simple estimate drawn from their abundance assuming a homogeneous distribution. In particular, especially at high redshifts (z ≥ 20), the halos are closely clustered, with an average separation of roughly ∼ 500 pc. From this we can estimate the average speed at which the blast wave from a Pop III supernova in one minihalo impacts its nearest neighboring minihalo, using the results presented in Figure 11. As can be seen from that Figure, the typical speeds with which the shock propagates at rsh ∼ 500 pc from the explosion site are roughly 20-40 km s−1. This is high enough to disrupt the gas near the virial radius of a neighboring halo, but not high enough to mix the metal-enriched ejecta with the dense star-forming gas in the interior of the halo at r < 0.1rvir, as given by equation (40). Indeed, a similar result is found for the case of vsh = 30 km s−1 in simulations in which the mixing of the gas is resolved, as shown in Figure 13. Therefore, we conclude that the inefficiency of mixing poses a substantial challenge for the metals ejected in Pop III supernova explosions to enrich other star-forming halos and prevent Pop III star formation from occurring (see also Wyithe & Cen 2007; Wise & Abel 2008; Greif et al. 2010).
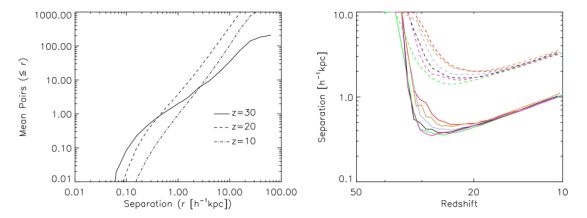 |
Figure 14. Clustering of Pop III star-forming minihalos in a simulation of the formation of a Milky Way-like halo. Left panel: mean number of progenitor halo pairs, as a function of their physical separation at the three redshifts indicated in the panel. Right panel: mean separation of progenitor haloes in each of several similar simulations. Each halo has one neighbour within the distance given by the solid line, and 10 neighbours within the distance given by the dashed lines. While the radiation produced by one Pop III star in a given halo is likely to impact its neighbors and perhaps delay star formation, as discussed in Section 2, it is in general unlikely that the metal-enriched ejecta from Pop III supernovae will mix with the dense star-forming gas in neighboring halos. From Gao et al. (2010). |
While here we have presented simple analytical estimates of the degree to which metals ejected in the first supernovae are mixed with the primordial gas via hydrodynamical instabilities, both in the IGM and in neighboring minihalos, other processes also contribute to mixing metals into the primordial gas (see e.g. Ferrara et al. 2000; Karlsson et al. 2011; Maio et al. 2011). Perhaps chief among these is the turbulence which develops as gas rapidly flows into the centers of the atomic cooling halos in which the first galaxies form (Wise & Abel 2007b; Greif et al. 2008) and acts to enhance the rate at which mixing takes place on small scales via diffusion (see e.g. Tenorio-Tagle 1996; Klessen & Lin 2003; Karlsson 2005; Pan & Scalo 2007). Once star formation begins in these halos, turbulent mixing is also facilitated by the energy injected by supernova explosions (e.g. Mori et al. 2002; Wada & Venkatesan 2003; Vasiliev et al. 2008), and the fraction of un-enriched primordial gas in the first galaxies is expected to continually drop with time (e.g. de Avillez & Mac Low 2002). We turn next to discuss the impact that the first metals, once mixed into the primordial gas, have on the cooling of the gas and so on the nature of star formation.
3.3. Metal Cooling in the First Galaxies
In Section 2.1 we discussed how cooling by the molecule HD, which may be formed in abundance in partially ionized primordial gas, can lower the temperature of the gas to the lowest temperature possible via radiative cooling, that of the CMB. Here we draw on the same formalism introduced there to show how just a small amount of metals mixed into the primordial gas can allow it to cool to low temperatures even more efficiently. While a number of heavy elements contribute to the cooling of low-metallicity gas, here we shall take a simplified approach and focus only on cooling by carbon, which is likely to have been released in abundance in the first supernova explosions (e.g. Heger & Woosley 2002, 2010; Tominaga et al. 2007).
To begin, we note that once the first generations of stars form and a background radiation field is established, as discussed in Section 2.2, besides dissociating H2 this background radiation field can easily ionize neutral carbon (e.g. Bromm & Loeb 2003b). This makes available the potent coolant C ii which, even in the Galaxy today, is important for cooling the gas to very low temperatures in dense star-forming clouds (e.g. Stahler & Palla 2004).
To see how the presence of C ii in the first galaxies affects the cooling of the gas, we first note that at low temperatures this ion is readily collisionally excited from its ground 2P1/2 state to the first excited 2P3/2 state. The energy difference between these two fine-structure states is just
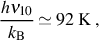 |
(41) |
where here ν10 denotes the frequency of the photon emitted in the radiative decay of the first excited state back to the ground state. As the energy difference is even smaller than that between the ground and first excited rotational states of HD, C ii offers the potential to more efficiently cool the gas than HD, as even lower energy collisions are able to excite the ion. In addition, the Einstein coefficient for spontaneous radiative decay is A10 = 2.4 × 10−6 s−1, almost two orders of magnitude higher than that for the J = 1 → 0 transition of HD.
We can obtain a conservative lower limit for the cooling rate of C ii via this transition by considering the cooling of gas in the low density regime, in which the rate of collisional excitations is balanced by the rate of radiative decays, that is at densities n < ncrit, where the critical density ncrit is defined as that above which the rate of collisional deexcitations exceeds the rate of radiative deexcitations. For the transition of C ii that we are considering, ncrit = 3 × 103 cm−3. In this case, the cooling rate is given as (e.g. Stahler & Palla 2004)
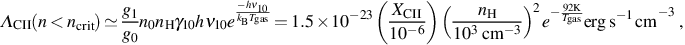 |
(42) |
where γ10nh = 6 × 10−10 nh s−1 is the rate at which a given C ii ion in the ground state is excited due to a collision with a neutral hydrogen atom, gi is the statistical weight of the ith excited state, XCII is the fractional abundance of C ii relative to hydrogen, and Tgas is the temperature of the gas. For densities n > ncrit, in turn, the cooling rate varies linearly with the density of the gas, since in this case the level populations are in LTE, as given by equation (10), and the rate of radiative decay is no longer balanced by the rate of collisional excitation. In this case, we have
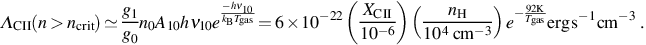 |
(43) |
The right panel of Figure 15 shows, along with the cooling rates of a number of other metal species, the cooling rate due to C ii given above, as a function of gas temperature, for n < ncrit. The cooling rates of oxygen, iron, and silicon that are shown can be obtained following the first part of equation (42) using the atomic data corresponding to those elements (see e.g. Santoro & Shull 2006; Maio et al. 2007). We note, however, that the cooling rate per C ii ion is higher than that of any of the other metal species shown, as well as being at least an order of magnitude higher than the cooling rate per molecule of any of the primordial species shown in the left panel, at temperatures Tgas ≤ 100 K. Therefore, we can focus on this chemical species as a means to derive a simple estimate of the minimum abundance of heavy elements required to significantly alter the cooling properties of the primordial gas, and perhaps thereby alter the nature of star formation.
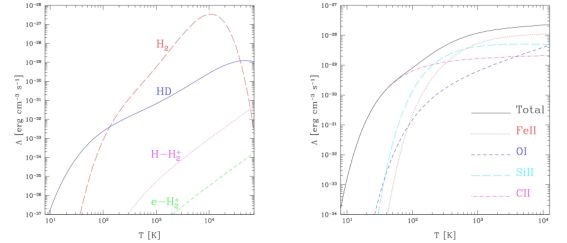 |
Figure 15. Left panel: Cooling rates for primordial gas with a hydrogen number density nh = 1 cm−3 and the following fractions for the different species: XHD = 10−8 , XH2 = 10−5 , XH2+ = 10−13, Xe− = 10−4. The H2 cooling rate (long-dashed line) is plotted together with those of HD (solid), H-impact H2+ (dotted line) and e-impact H2+ (short-dashed line). Right panel: Cooling rates of various metal species as a function of temperature, for a gas also with hydrogen number density nh = 1 cm−3; for each metal species a fractional abundance of 10−6 is assumed. The cooling rate per C ii ion is higher than the cooling rate per particle of any of the other species shown here, at Tgas ≤ 100 K. From Maio et al. (2007). |
A rough estimate of the minimum carbon abundance required for the characteristic fragmentation mass to change from the relatively large value expected for primordial gas in the case of Pop III.1 star formation can be found by considering the properties of the primordial gas when fragmentation takes place. At this stage, the so-called loitering phase in the collapse of the primordial gas in minihalos, Tgas ∼ 200 K and n ∼ 104 cm−3 (e.g. Abel et al. 2002; Bromm et al. 2002). Hence, the Jeans mass (equation 4) is of the order of 100 M⊙ and, if the gas does not cool efficiently then a massive Pop III star, or perhaps a binary or small multiple system, will likely form (e.g. Turk et al. 2009; Stacy et al. 2010; Clark et al. 2011a; Greif et al. 2011). However, if the gas cools to lower temperatures, then the Jeans mass becomes smaller and the gas is expected to fragment into smaller clumps; in turn, this is expected to translate into the formation of less massive stars.
Following the discussion in Section 2.1, we note that in order for the gas to cool efficiently at this stage, the cooling rate must exceed the rate at which the gas is heated adiabatically by compression during its collapse (Bromm & Loeb 2003b). Taking the adiabatic heating rate to be Γad ∼ 1.5nkBTgas / tff, where tff ≃ (G ρ)−1/2 is the free-fall time and the cooling rate ΛCII is given by equation (43), this condition is satisfied if XCII > 7 × 10−8. Assuming that all carbon is in the form of C ii and taking it that the solar abundance of carbon is ∼ 3 × 10−4 by number, this yields a critical carbon abundance of [C/H]crit ≃ -3.5. 10
While other elements, such as oxygen, iron, and silicon, also contribute to the cooling of metal-enriched gas, this abundance of carbon relative to the solar value is similar to what is found for the overall critical metallicity Zcrit / Z⊙ ∼ 10−3.5 that is typically found in detailed calculations including atomic cooling 11 (e.g. Bromm et al. 2001; Omukai et al. 2005; Smith & Sigurdsson 2007; Smith et al. 2009; Aykutalp & Spaans 2011; but see Jappsen et al. 2009a, b). Figure 16 shows the results of one such calculation, in which the temperature evolution of the gas is modeled as it collapses to high densities, for various values of the metallicity of the gas. For the case of metal-free gas, the temperature of the gas increases after the loitering phase at n ∼ 104 cm−3; in this case, fragmentation at mass scales smaller than of the order of 100 M⊙ is thus unlikely. However, when Z ≥ 10−4 Z⊙, close the value we found above for the critical carbon abundance, the gas cools as it collapses to densities n > 104 cm−3 and consequently the fragmentation scale decreases appreciably compared to the primordial case. Hence, less massive stars are likely to form in gas enriched to this level.
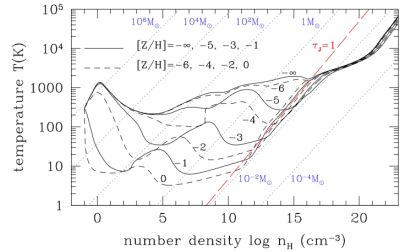 |
Figure 16. Temperature evolution of collapsing prestellar clouds with different metallicities, as a function of density. The evolutionary tracks of clouds with metallicities [Z/H] = -∞ (Z=0), -5, -3, and -1 (-6, -4, -2, and 0) are shown by solid (dashed) lines. The dotted lines denote various values of the Jeans mass MJ. Near the critical density of H2, n ∼ 104 cm−3, at which the cooling of primordial gas becomes less efficient, the temperature continues to drop as the gas collapses to higher densities for metallicities Z ≥ 10−4 Z⊙; this is due to the cooling provided by C ii and other atomic species, as discussed in the text. At higher densities, n ≥ 1010 cm−3, the gas is able to cool efficiently even at a metallicity of Z ∼ 10−5 Z⊙, if dust is present, as is the case in the calculation shown here. From Omukai et al. (2005). |
We note also a second drop in the temperature of the gas at higher densities for even lower metallicities in Figure 16; this decrease in temperature for Z ≥ 10−5 Z⊙ occurs because of dust cooling. While the dust fraction in extremely metal-poor gas is not known, dust formation in early supernovae (e.g. Nozawa et al. 2003; Schneider et al. 2004; Cherchneff & Dwek 2010) may yield it high enough for the thermal evolution of the gas to be affected at n ≥ 1010 cm−3, as shown here, even for such extremely low metallicities. In this case, the critical metallicity for low-mass star formation may be smaller than we estimated above for the case of cooling by atomic species such as C ii, perhaps as low as Zcrit ∼ 10−5 Z⊙ (see e.g. Schneider et al. 2006; Clark et al. 2008).
In general, simulations of the evolution of low-metallicity star-forming gas give the same general result that the fragmentation scale, as well as the protostellar accretion rate, is higher for metal-free gas than for metal-enriched gas, and hence that the typical masses of Pop III stars are higher than those of Pop II stars (e.g. Bromm et al. 2001; Smith et al. 2007; but see Jappsen et al. 2009a, b). However, as shown in Figure 17, recent very high resolution cosmological simulations suggest that low-mass protostars formed in clusters may be ejected from the dense central regions of primordial minihalos due to dynamical interactions, in which case their growth may be limited due to the accretion of gas being dramatically slowed (Greif et al. 2011; see also Clark et al. 2011a). In this event, it is possible that low-mass stars may indeed form from primordial gas, although they may only constitute a small fraction of all Pop III stars (e.g. Tumlinson et al. 2006; Madau et al. 2008). If their masses were less than ≃ 0.8 M⊙, then such low-mass stars could be detectable as un-enriched dwarfs or red giants in the Galaxy even today (Johnson & Khochfar 2011), although there is a strong possibility that their surfaces would be enriched due to accretion of metals from the interstellar medium (see e.g. Suda et al. 2004; Frebel et al. 2009; Komiya et al. 2010). To date, however, no low-mass stars with overall metallicity below of the order of 10−4 Z⊙ have been detected, which is consistent with the critical metallicity being set by cooling due to atomic species such as carbon and oxygen (see Frebel et al. 2007).
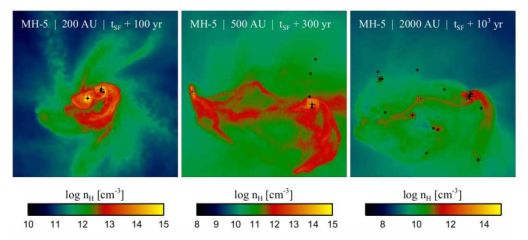 |
Figure 17. The state of the central gas cloud in a primordial minihalo at 100 yr (left panel), 300 yr (middle panel), and 103 yr (right panel) after the formation of the first protostar in a very high resolution cosmological simulation. Shown here is the hydrogen density projected along the line of sight. Blackdots, crosses and stars denote protostars with masses below 1M⊙, between 1M⊙ and 3M⊙, and above 3M⊙, respectively. The gas fragments into a relatively rich cluster of protostars with a range of masses. Dynamical interactions can lead to the ejection of low-mass protostars, while more massive protostars tend to remain at the center of the cloud and continue to accrete from the surrounding envelope of gas. Thus, while massive primordial stars are likely to form in such clusters, some fraction of Pop III stars with masses below ∼ 1 M⊙ may also form. From Greif et al. (2011). |
While the additional avenues for radiative cooling provided by even trace amounts of metals clearly alter the evolution of the gas and the process of star formation, other factors also play a role in dictating the thermal and dynamical state of the gas in the first galaxies. Magnetic fields may impede the large-scale collapse of the gas into dark matter halos (e.g. Schleicher et al. 2009; Rodrigues et al. 2010; de Souza et al. 2011) or alter the collapse of the gas at smaller scales during star formation (e.g. Kulsrud et al. 1997; Silk & Langer 2006; Xu et al. 2008; Schleicher et al. 2010a). Also, cosmic rays generated in the first supernova explosions are an additional source of ionization that can speed the formation of molecules and so enhance the cooling of the gas (see Vasiliev & Shchekinov 2006; Stacy & Bromm 2007; Jasche et al. 2007). Finally, the impact of the turbulence generated by both the accretion of gas from the IGM and supernovae in the first galaxies may dramatically impact the process of star formation, in general acting to decrease the mass scale at which the gas fragments and forms stars (e.g. Padoan et al. 2007; Clark et al. 2008, 2011b; Prieto et al. 2011).
10 Here we use the common notation for abundance ratios relative to those of the sun given by [X/Y] = log10(NX/NY) - log10(NX / NY)⊙, where NX and NY are the numbers of nuclei of elements X and Y, respectively. Back.
11 As the cooling rates of the various atomic species each contribute separately to the total cooling rate, it is the combination of their individual abundances which determines whether the 'critical metallicity' is achieved (see e.g. Frebel et al. 2007). Back.